1.3.1 线段的垂直平分线课件

(共15张PPT)
数学北师大版

八年级
1.3线段的垂直平分线第一课时
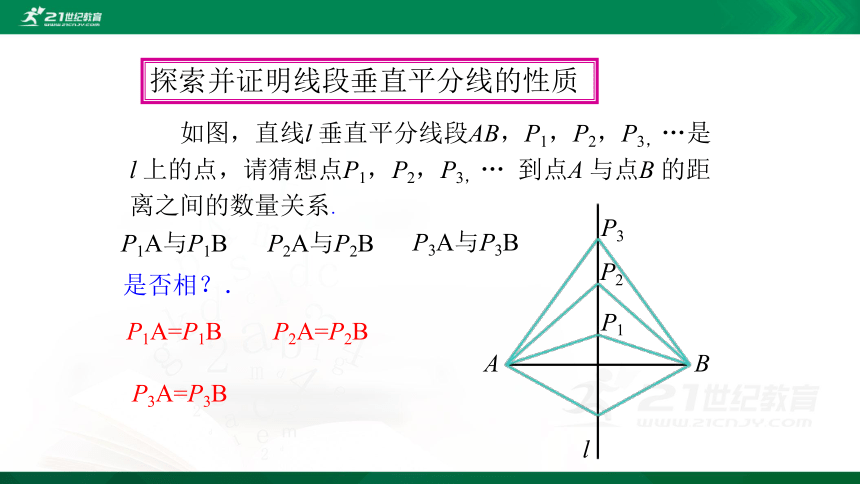
探索并证明线段垂直平分线的性质
　　如图，直线l 垂直平分线段AB，P1，P2，P3，…是
l 上的点，请猜想点P1，P2，P3，… 到点A 与点B 的距
离之间的数量关系．
　　是否相？．
A
B
l
P1
P2
P3
P1A=P1B
P2A=P2B
P3A=P3B
P1A与P1B
P2A与P2B
P3A与P3B
线段垂直平分线的性质：
定理：线段垂直平分线上的点到线段两个端点的距离相等．
已知：如图，直线MN⊥AB，垂足是C，且AC=BC，P是MN上的点．求证：PA=PB．








N

A

P

B

C

M

证明：∵MN⊥AB，
∴∠PCA=∠PCB=90°
∵AC=BC，PC=PC,
∴△PCA≌△PCB(SAS) ；
∴PA=PB(全等三角形的对应边相等)．
你能写出上面这个定理的逆命题吗?它是真命题吗?
如果有一个点到线段两个端点的距离相等，那么这个点在这条线段的垂直平分线上．
即到线段两个端点的距离相等的点在这条线段的垂直平分线上．
当我们写出逆命题时，就想到判断它的真假．如果真，则需证明它；如果假，则需用反例说明．
已知：线段AB，点P是平面内一点且PA=PB．
求证：P点在AB的垂直平分线上．
证明：过点P作已知线段AB的垂线PC，
PA=PB，PC=PC，
∴Rt△PAC≌Rt△PBC(HL)．
∴AC=BC，
即P点在AB的垂直平分线上．

C








B

P

A
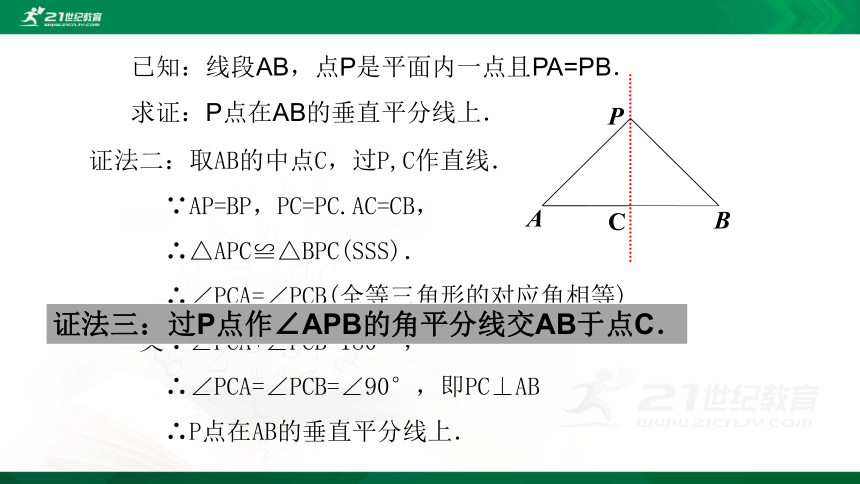
证法二：取AB的中点C，过P,C作直线．
∵AP=BP，PC=PC.AC=CB，
∴△APC≌△BPC(SSS)．
∴∠PCA=∠PCB(全等三角形的对应角相等)
又∵∠PCA+∠PCB=180°，
∴∠PCA=∠PCB=∠90°，即PC⊥AB
∴P点在AB的垂直平分线上．

C






B

P

A
已知：线段AB，点P是平面内一点且PA=PB．
求证：P点在AB的垂直平分线上．
证法三：过P点作∠APB的角平分线交AB于点C．
探索并证明线段垂直平分线的判定
　　用数学符号表示为：
∵　PA =PB，
∴　点P 在AB 的垂直平分线上．
　　与一条线段两个端点距离相
等的点，在这条线段的垂直平分
线上．

P
A
B


C
例1 已知在△ABC中，AB=AC，O是△ABC内一 点，且OB=OC.
求证：直线AO垂直平分线段BC.
证明：∵ AB=AC,
∴ 点A在线段BC的垂直平分线上.


同理，点O在线段BC的垂直平分线上.
∴ 直线AO是线段BC的垂直平分线.
（两点确定一条直线）
（到一条线段两个端点距离相等的点， 在这条线段的垂直平分线上）
A
C

B
O
【例2】如图，在Rt△ABC中，∠C＝90°，∠CAB的平分线AD交BC于点D，若DE垂直平分AB，求∠B的度数．
×
×
║
║











1.如图，在△ABC中，AB＝BC，∠ABC＝110°，AB的垂直平分线DE交AC于点D，连接BD，求∠ABD的度数．
课堂练习




解：∵　AD⊥BC，BD =DC
∴　AD 是BC 的垂直平分线
∴　AB =AC
∵　点C 在AE 的垂直平分线上
∴　AC =CE． ∴　AB =AC =CE
2　如图，AD⊥BC，BD =DC，点C 在AE 的垂直平分线上，AB，AC，CE 的长度有什么关系？AB+BD与DE 有什么关系？



A
B
C
D


E
∵　AB =CE，BD =DC，∴　AB +BD =CD +CE．
即　AB +BD =DE ．
3．如图，在△ABC中，∠C＝90°，∠B＝15°，AB的垂直平分线交BC于点D，交AB于点E，DB＝10.求∠ADC的度数和边AC的长．





4．如图，在△ABC中，AB的垂直平分线MN交AB于点D，交AC于点E，且AC＝15 cm，△BCE的周长等于25 cm. (1)求BC的长； (2)若∠A＝36°，AB＝AC，求证：BC＝BE.
解：∵DE是AB的垂直平分线，∴AE＝BE. ∵△BCE的周长等于25 cm.∴BE＋EC＋BC＝25 cm， ∴AE＋EC＋BC＝25 cm，即AC＋BC＝25 cm. ∵AC＝15 cm，∴BC＝10 cm.









(2)证明：∵AB＝AC，∠A＝36°，∴∠ABC＝∠C＝72°. ∵DE是AB的垂直平分线，∴AE＝BE， ∴∠A＝∠ABE＝36°， ∴∠BEC＝∠A＋∠ABE＝72°，∴∠C＝∠BEC，∴BC＝BE.
谢谢
21世纪教育网（www.21cnjy.com) 中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php