高二物理选修3-4 11.4 单摆 课件(27张ppt人教版)
文档属性
| 名称 | 高二物理选修3-4 11.4 单摆 课件(27张ppt人教版) |

|
|
| 格式 | zip | ||
| 文件大小 | 804.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-02-19 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
高考导航
1.基本考察点:周期和摆长的关系;
2.重难点:单摆的周期性、摆钟的快慢、用单摆测重力加速度;
3.题型及难度:考查形式多样,有选择题,也有计算题,难度中等。
11.4 单摆
1.定义:一根细线悬挂一个小球,如果细线的质量与小球的质量相比可以忽略,
球的直径与线的长度相比也可以忽略,这样的装置就叫做单摆。
一、单摆
说明:单摆是理想化模型:
2.实际摆看成单摆的条件
①摆线质量与小球质量相比小很多, 忽略摆线的质量
②摆球所受阻力远小于摆球重力及绳的拉力, 忽略空气阻力
③当摆线的形变量比摆线长度小的多, 忽略摆线形变 ④摆球的直径 d远小于单摆的摆长L 将摆球看作质点
注意:实际做成的单摆,悬线伸缩越小,小球的质量越大,体积越小,
直径与线长相比可忽略,则越接近理想化的单摆。
例1.(多选)单摆是为了研究振动而抽象出的理想化模型,其理想化条件是( )
A.摆线质量不计
B.摆线长度不伸缩
C.摆球的直径比摆线长度短得多
D.只要是单摆的运动就是一种简谐运动
ABC
C
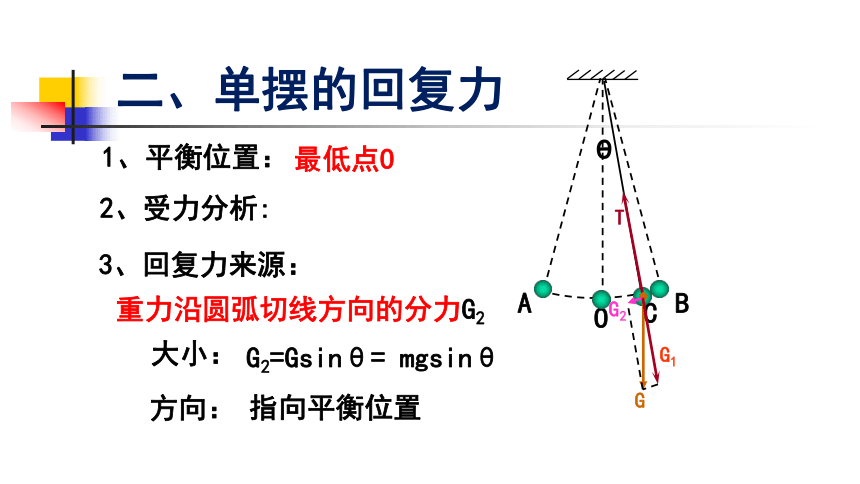
2、受力分析:
B
A
O
3、回复力来源:
重力沿圆弧切线方向的分力G2
1、平衡位置:
大小:
G2=Gsinθ= mgsinθ
方向:
指向平衡位置
θ
T
G
G2
G1
最低点O
二、单摆的回复力
?
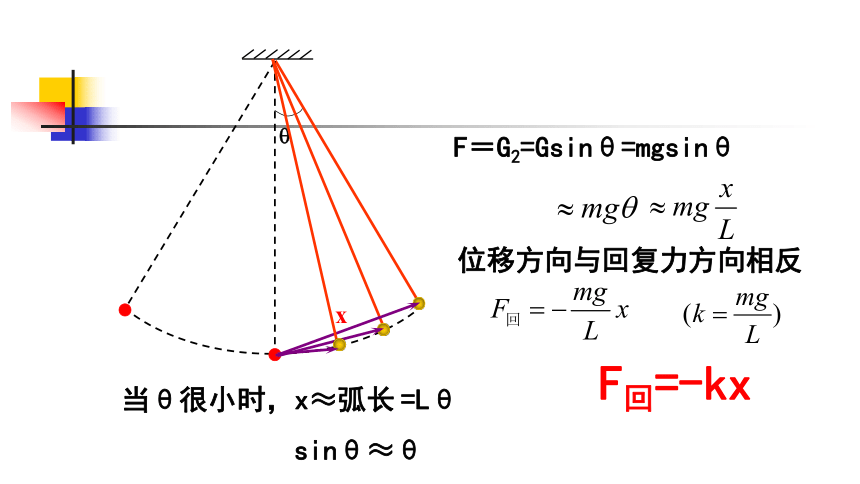
x
当θ很小时,x≈弧长
F=G2=Gsinθ=mgsinθ
位移方向与回复力方向相反
sinθ≈θ
=Lθ
F回=-kx
结 论:
在摆角很小的情况下,摆球所受的回复力跟位移大小成正比,方向始终指向平衡位置(即与位移方向相反),因此单摆做简谐运动
一般摆角θ 5°
F回=-kx
二、单摆的回复力
特别提醒
1.所谓平衡位置,是指摆球静止时,摆线拉力与小球所受重力平衡的位置,并不是指摆动过程中摆球受力平衡的位置。摆球摆动到平衡位置时,回复力为零,但有指向悬点的向心力作用。
2.回复力是由摆球受到的重力沿圆弧切线方向的分力F= mgsinθ提供的,不可误认为回复力是重力和摆线拉力的合力。
二、单摆的回复力
例2.关于做简谐运动的单摆,下列说法正确的是( )
A.单摆经过平衡位置时合力为零
B.摆角小于5°时,摆球合力的大小跟摆球相对平衡位置的位移大小成正比
C.只有在最高点时,回复力才等于重力和摆线拉力的合力
D.摆球在任意位置处,回复力都不等于重力和摆线拉力的合力
C
猜想:单摆振动的周期可能与哪些因素有关呢?
1、周期与振幅是否有关 ?
2、周期与摆球的质量是否有关 ?
3、周期与摆长是否有关 ?
4、周期与重力加速度是否有关?
探究方法:控制变量法
三、单摆的周期
结论:
4、与当地的重力加速度有关——重力加速度越大,周期越小
单摆振动的周期
1、与振幅无关——单摆的等时性
2、与摆球的质量无关
3、与摆长有关——摆长越长,周期越大
三、单摆的周期
1.单摆振动的周期公式:
荷兰物理学家惠更斯首先得出
三、单摆的周期
2.决定因素(1)摆长
(2)当地重力加速度
单摆做简谐运动的振动周期跟摆长的平方根成正比,
跟重力加速度的平方根成反比,与振幅和摆球质量无关。
(1)l 为单摆的摆长,是指悬点(圆心)到摆球重心的长度 l =l 绳+r球。
(3)摆长、重力加速度都一定时,周期和频率也一定,通常 称为单摆的固有周期和固有频率,与振幅无关。
(2)单摆周期与摆长和重力加速度有关,与振幅和质量无关。
三、单摆的周期
3、单摆周期公式的理解
4、单摆周期公式的应用
(1)计时器:利用它的等时性计时,制成计时仪器,如摆钟等。
(2)测重力加速度:由单摆周期公式可得g=,只要测出单摆的摆长和周期T,就可算出当地的重力加速度。
(4)周期为2s的单摆叫做秒摆。秒摆的摆长约为1m.)
例3.有一单摆,其摆长l=1.02m,摆球的质量m=0.10kg,已知单摆做简谐运动,单摆振动30次用的时间t=60.8s,试求:
(1)当地的重力加速度是多大?
(2)如果将这个摆改为秒摆,摆长应怎样改变?改变多少?
(1)重力加速度g为9.79m/s2;
(2)如果将这一单摆改成秒摆,摆长应缩短0.027m.
如图,摆球可视为质点,各段绳长均为L,甲、乙摆球做垂直纸面的小角度摆动,丙图中球在纸面内做小角度的摆动,O`为垂直纸面的钉子,而且OO`=L/3,求各摆的周期。
α
α
α
α
L
L
L
L
L
O
O`
L/3
L
甲
乙
丙
四、单摆振动中的等效问题
摆长(或等效摆长)
重力加速度
(或等效重力加速度)
1.等效摆长:
摆球重心到
摆动圆弧圆心
的距离。
A
例4.
注意:是小角度摆动
2、等效重力加速度
1.公式中g应理解为等效重力加速度,实际中不一定为9.8m/s2,而由
单摆所处的位置、摆球的受力情况及系统运动的加速度情况决定。
2.求等效重力加速度的经验公式: ,即等效重力加速度等于摆球在平衡位置不摆动时,
摆线的拉力与摆球质量的比值.(具体问题要看环境因素对简谐运动的回复力有无影响)
四、单摆振动中的等效问题
3.确定等效重力加速度的方法:
(1)确定摆球的平衡位置
(2)确定摆球静止在平衡位置时摆线上的拉力F
(3)等效重力加速度g’=F/m
2、等效重力加速度 理解
重力的分力
对简谐运动的回复力无影响
3.模型等效
例5. 如图所示,光滑圆弧槽半径为R,A为最低点,C到A距离远小于R,两质点B和C都由静止开始释放,问哪一个小球先到A点?
讨论:要使两球在A点相遇,B点向上移动,问B球高度h应为多少?
四、单摆振动中的等效问题
例6.在图中的几个相同的单摆在不同的条件下,关于它们的周期关系,
判断正确的是( )
A.T1>T2>T3>T4 B.T1<T2=T3<T4
C.T1>T2=T3>T4 D.T1<T2<T3<T4
C
B
课堂练习
1.
L
L
L
L
L
2.一个充满水的塑料桶用绳子悬挂在固定点上摆动。若水桶是漏的,则随着水的流失,其周期即将( )
A.总是变大 B.总是变小
C.先变小在变大 D.先变大再变小
D
BC
3.
α
o
4.如图,一小球用长为L的细线系于与水平面成α角的光滑斜面内,小球呈平衡状态。若使细线偏离平衡位置,其偏角小于5o,然后将小球由静止释放,则小球第一次到达最低点所需的时间为多少?
小结:
在最大摆角很小的情况下,单摆做简谐运动.
摆线:
质量不计
长度远大于小球直径
不可伸缩
摆球:
质点(体积小 质量大)
1.单摆模型
2.单摆的回复力:
单摆做简谐运动的周期跟摆长的平方根成正比,跟重力加速度的平方根成反比,跟振幅、摆球的质量无关.
3.单摆的周期:
作业
1.先复习今天所讲基础内容;
2.电子版作业的答案写在作业纸上并且拍照 上传照片到微信群;
3.预习单摆实验并做课后习题。
高考导航
1.基本考察点:周期和摆长的关系;
2.重难点:单摆的周期性、摆钟的快慢、用单摆测重力加速度;
3.题型及难度:考查形式多样,有选择题,也有计算题,难度中等。
11.4 单摆
1.定义:一根细线悬挂一个小球,如果细线的质量与小球的质量相比可以忽略,
球的直径与线的长度相比也可以忽略,这样的装置就叫做单摆。
一、单摆
说明:单摆是理想化模型:
2.实际摆看成单摆的条件
①摆线质量与小球质量相比小很多, 忽略摆线的质量
②摆球所受阻力远小于摆球重力及绳的拉力, 忽略空气阻力
③当摆线的形变量比摆线长度小的多, 忽略摆线形变 ④摆球的直径 d远小于单摆的摆长L 将摆球看作质点
注意:实际做成的单摆,悬线伸缩越小,小球的质量越大,体积越小,
直径与线长相比可忽略,则越接近理想化的单摆。
例1.(多选)单摆是为了研究振动而抽象出的理想化模型,其理想化条件是( )
A.摆线质量不计
B.摆线长度不伸缩
C.摆球的直径比摆线长度短得多
D.只要是单摆的运动就是一种简谐运动
ABC
C
2、受力分析:
B
A
O
3、回复力来源:
重力沿圆弧切线方向的分力G2
1、平衡位置:
大小:
G2=Gsinθ= mgsinθ
方向:
指向平衡位置
θ
T
G
G2
G1
最低点O
二、单摆的回复力
?
x
当θ很小时,x≈弧长
F=G2=Gsinθ=mgsinθ
位移方向与回复力方向相反
sinθ≈θ
=Lθ
F回=-kx
结 论:
在摆角很小的情况下,摆球所受的回复力跟位移大小成正比,方向始终指向平衡位置(即与位移方向相反),因此单摆做简谐运动
一般摆角θ 5°
F回=-kx
二、单摆的回复力
特别提醒
1.所谓平衡位置,是指摆球静止时,摆线拉力与小球所受重力平衡的位置,并不是指摆动过程中摆球受力平衡的位置。摆球摆动到平衡位置时,回复力为零,但有指向悬点的向心力作用。
2.回复力是由摆球受到的重力沿圆弧切线方向的分力F= mgsinθ提供的,不可误认为回复力是重力和摆线拉力的合力。
二、单摆的回复力
例2.关于做简谐运动的单摆,下列说法正确的是( )
A.单摆经过平衡位置时合力为零
B.摆角小于5°时,摆球合力的大小跟摆球相对平衡位置的位移大小成正比
C.只有在最高点时,回复力才等于重力和摆线拉力的合力
D.摆球在任意位置处,回复力都不等于重力和摆线拉力的合力
C
猜想:单摆振动的周期可能与哪些因素有关呢?
1、周期与振幅是否有关 ?
2、周期与摆球的质量是否有关 ?
3、周期与摆长是否有关 ?
4、周期与重力加速度是否有关?
探究方法:控制变量法
三、单摆的周期
结论:
4、与当地的重力加速度有关——重力加速度越大,周期越小
单摆振动的周期
1、与振幅无关——单摆的等时性
2、与摆球的质量无关
3、与摆长有关——摆长越长,周期越大
三、单摆的周期
1.单摆振动的周期公式:
荷兰物理学家惠更斯首先得出
三、单摆的周期
2.决定因素(1)摆长
(2)当地重力加速度
单摆做简谐运动的振动周期跟摆长的平方根成正比,
跟重力加速度的平方根成反比,与振幅和摆球质量无关。
(1)l 为单摆的摆长,是指悬点(圆心)到摆球重心的长度 l =l 绳+r球。
(3)摆长、重力加速度都一定时,周期和频率也一定,通常 称为单摆的固有周期和固有频率,与振幅无关。
(2)单摆周期与摆长和重力加速度有关,与振幅和质量无关。
三、单摆的周期
3、单摆周期公式的理解
4、单摆周期公式的应用
(1)计时器:利用它的等时性计时,制成计时仪器,如摆钟等。
(2)测重力加速度:由单摆周期公式可得g=,只要测出单摆的摆长和周期T,就可算出当地的重力加速度。
(4)周期为2s的单摆叫做秒摆。秒摆的摆长约为1m.)
例3.有一单摆,其摆长l=1.02m,摆球的质量m=0.10kg,已知单摆做简谐运动,单摆振动30次用的时间t=60.8s,试求:
(1)当地的重力加速度是多大?
(2)如果将这个摆改为秒摆,摆长应怎样改变?改变多少?
(1)重力加速度g为9.79m/s2;
(2)如果将这一单摆改成秒摆,摆长应缩短0.027m.
如图,摆球可视为质点,各段绳长均为L,甲、乙摆球做垂直纸面的小角度摆动,丙图中球在纸面内做小角度的摆动,O`为垂直纸面的钉子,而且OO`=L/3,求各摆的周期。
α
α
α
α
L
L
L
L
L
O
O`
L/3
L
甲
乙
丙
四、单摆振动中的等效问题
摆长(或等效摆长)
重力加速度
(或等效重力加速度)
1.等效摆长:
摆球重心到
摆动圆弧圆心
的距离。
A
例4.
注意:是小角度摆动
2、等效重力加速度
1.公式中g应理解为等效重力加速度,实际中不一定为9.8m/s2,而由
单摆所处的位置、摆球的受力情况及系统运动的加速度情况决定。
2.求等效重力加速度的经验公式: ,即等效重力加速度等于摆球在平衡位置不摆动时,
摆线的拉力与摆球质量的比值.(具体问题要看环境因素对简谐运动的回复力有无影响)
四、单摆振动中的等效问题
3.确定等效重力加速度的方法:
(1)确定摆球的平衡位置
(2)确定摆球静止在平衡位置时摆线上的拉力F
(3)等效重力加速度g’=F/m
2、等效重力加速度 理解
重力的分力
对简谐运动的回复力无影响
3.模型等效
例5. 如图所示,光滑圆弧槽半径为R,A为最低点,C到A距离远小于R,两质点B和C都由静止开始释放,问哪一个小球先到A点?
讨论:要使两球在A点相遇,B点向上移动,问B球高度h应为多少?
四、单摆振动中的等效问题
例6.在图中的几个相同的单摆在不同的条件下,关于它们的周期关系,
判断正确的是( )
A.T1>T2>T3>T4 B.T1<T2=T3<T4
C.T1>T2=T3>T4 D.T1<T2<T3<T4
C
B
课堂练习
1.
L
L
L
L
L
2.一个充满水的塑料桶用绳子悬挂在固定点上摆动。若水桶是漏的,则随着水的流失,其周期即将( )
A.总是变大 B.总是变小
C.先变小在变大 D.先变大再变小
D
BC
3.
α
o
4.如图,一小球用长为L的细线系于与水平面成α角的光滑斜面内,小球呈平衡状态。若使细线偏离平衡位置,其偏角小于5o,然后将小球由静止释放,则小球第一次到达最低点所需的时间为多少?
小结:
在最大摆角很小的情况下,单摆做简谐运动.
摆线:
质量不计
长度远大于小球直径
不可伸缩
摆球:
质点(体积小 质量大)
1.单摆模型
2.单摆的回复力:
单摆做简谐运动的周期跟摆长的平方根成正比,跟重力加速度的平方根成反比,跟振幅、摆球的质量无关.
3.单摆的周期:
作业
1.先复习今天所讲基础内容;
2.电子版作业的答案写在作业纸上并且拍照 上传照片到微信群;
3.预习单摆实验并做课后习题。
