21.1 点和圆的位置关系 课件(20张)
文档属性
| 名称 | 21.1 点和圆的位置关系 课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 679.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
本节课应该学会的知识:
1.知道点和圆位置关系有哪几种?
2.理解掌握点和圆位置关系 大小关系
3.理解不在同一直线上的三个点确定一个圆并掌握它的运用.
4.了解三角形的外接圆和三角形外心的概念及不同的三角形外心位置
探究一:点和圆的位置关系
大家来参与向黑板上画的圆投掷粉笔头的活动
r
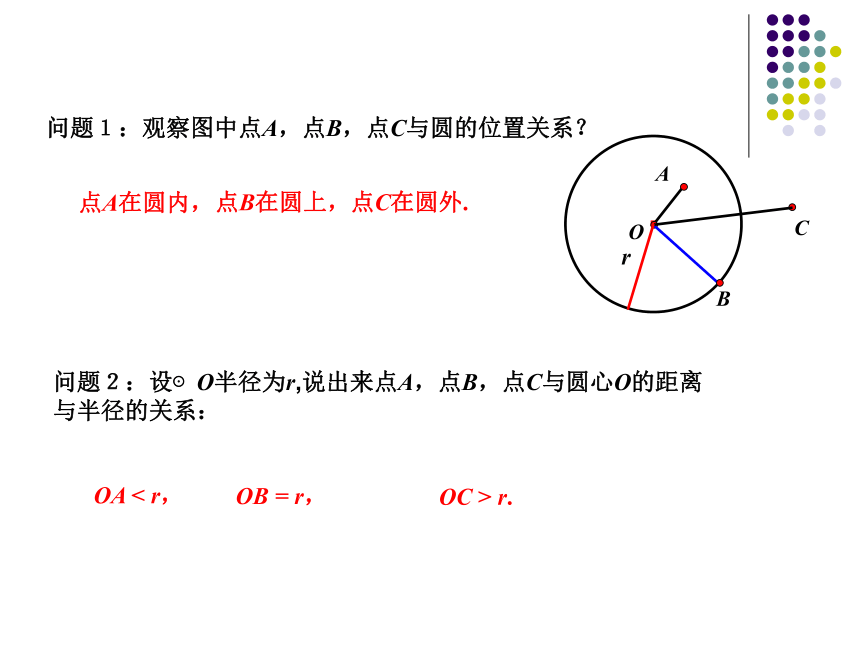
问题2:设⊙O半径为r,说出来点A,点B,点C与圆心O的距离与半径的关系:
·
C
O
A
B
OC > r.
问题1:观察图中点A,点B,点C与圆的位置关系?
点C在圆外.
点A在圆内,
点B在圆上,
OA < r,
OB = r,
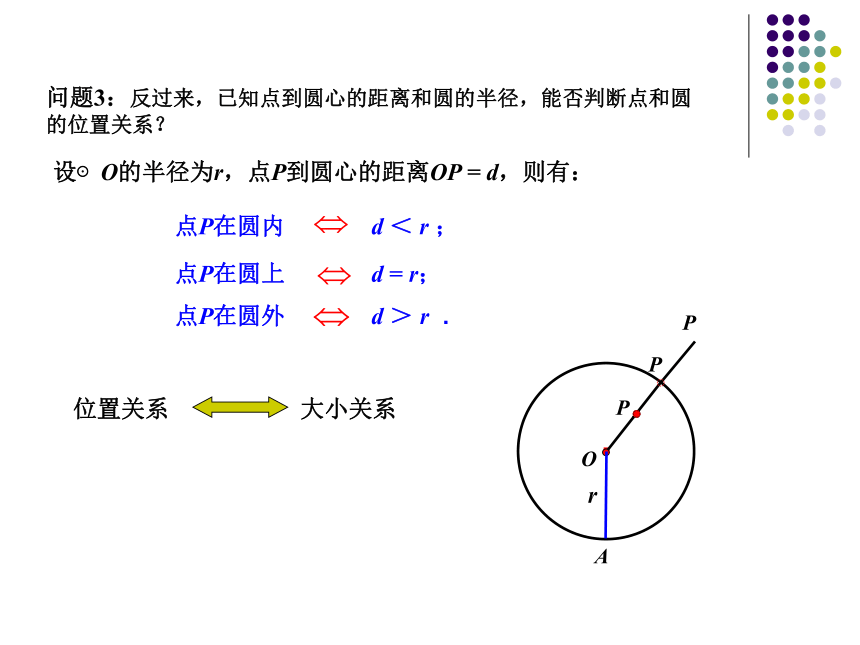
设⊙O的半径为r,点P到圆心的距离OP = d,则有:
r
·
O
A
问题3:反过来,已知点到圆心的距离和圆的半径,能否判断点和圆的位置关系?
P
P
P
位置关系 大小关系
巩固练习:
由d和r的大小关系判断点和圆的位置关系
1.P101页复习巩固1题
2. ⊙O的直径为10cm,点P到圆心O的距离d为10cm问点P与⊙O的位置关系是________
反之:知位置关系判断大小关系
已知点A在以O为圆心,3cm为半径的内,则点A到圆心O的距离d的取值范围是_________.
(1)如图,做经过已知点A的圆,这样的圆你能做出多少个?
(2)如图做经过已知点A、B的圆,这样的圆你能做出多少个?他们的圆心分布有什么特点?
·
·
·
·
·
·
A
B
A
活 动 二
2如何确定这个圆的圆心?
1.经过不在同一直线上三个点能作一个圆吗?
如图 三点A、B、C不在同一条直线上,因为所求的圆要经过A、B、C三点,所以圆心到这三点的距离相等,因此这个点要在线段AB的垂直的平分线上,又要在线段BC的垂直的平分线上.
结论:不在同一条直线上的三点确定一个圆.
·
C
O
A
B
l1
l2
3.以点O为圆心,OA(或OB、OC)为半径作圆,便可以作出经过A、B、C的圆.
1.分别连接AB、BC、AC;
2. 分别作出线段AB的垂直平分线l1和l2,设他们的交点为O ,则OA=OB=OC;
由于过A、B、C三点的圆的圆心只能是点O,半径等于OA,所以这样的圆只能有一个,即
提问:不在同一直线上四个点一定确定一个圆吗?
不在同一条直线上的三点确定一个圆-------------简单应用 (见学案)
2.三角形的外心(外接圆的心)是三角形三条边垂直平分线的交点。
C
O
A
B
1.经过三角形的三个顶点可以做一个圆
这个圆叫做三角形的外接圆
圆和三角形的位置关系:
这个三角形叫做这个圆的内接三角形。
结论(1)任意一个三角形的都有且只有一个外接圆
( 2)一个圆有无数个内接三角形
探究:活动三
1.锐角三角形的外心位置
2.直角三角形的外心位置
3.钝角三角形的外心位置
(见学案)
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
三角形外心位置特点:
本节课的收获:
1.设⊙O的半径为r,点P到圆心的距离OP = d,则有:
位置关系 大小关系
2.理解不在同一直线上的三个点确定一个圆并掌握它的运用.
(要求理解掌握上述知识)
3.了解三角形的外接圆和三角形外心的概念及不同的三角形外心的位置。
经过同一条直线三个点能作出一个圆吗?
活 动 四
提示:当直接证困难时,我们用反证法证明
所谓反证法,就是首先提出一个与
原命题结论相反的假设,然后从假
设出发,经过正确的推理,导出矛盾,
从而否定假设,进而肯定原命题的
一种方法.导出的矛盾主要有:与
已知条件矛盾;与已知的公理、定
理、定义、公式矛盾;与
反证法的三个步骤:
1、提出与原命题结论相反的假设
2、由假设出发,推出与已知条件或学过定理 的矛盾
3、由矛盾判定假设不成立,肯定结论正确
本节课应该学会的知识:
1.知道点和圆位置关系有哪几种?
2.理解掌握点和圆位置关系 大小关系
3.理解不在同一直线上的三个点确定一个圆并掌握它的运用.
4.了解三角形的外接圆和三角形外心的概念及不同的三角形外心位置
探究一:点和圆的位置关系
大家来参与向黑板上画的圆投掷粉笔头的活动
r
问题2:设⊙O半径为r,说出来点A,点B,点C与圆心O的距离与半径的关系:
·
C
O
A
B
OC > r.
问题1:观察图中点A,点B,点C与圆的位置关系?
点C在圆外.
点A在圆内,
点B在圆上,
OA < r,
OB = r,
设⊙O的半径为r,点P到圆心的距离OP = d,则有:
r
·
O
A
问题3:反过来,已知点到圆心的距离和圆的半径,能否判断点和圆的位置关系?
P
P
P
位置关系 大小关系
巩固练习:
由d和r的大小关系判断点和圆的位置关系
1.P101页复习巩固1题
2. ⊙O的直径为10cm,点P到圆心O的距离d为10cm问点P与⊙O的位置关系是________
反之:知位置关系判断大小关系
已知点A在以O为圆心,3cm为半径的内,则点A到圆心O的距离d的取值范围是_________.
(1)如图,做经过已知点A的圆,这样的圆你能做出多少个?
(2)如图做经过已知点A、B的圆,这样的圆你能做出多少个?他们的圆心分布有什么特点?
·
·
·
·
·
·
A
B
A
活 动 二
2如何确定这个圆的圆心?
1.经过不在同一直线上三个点能作一个圆吗?
如图 三点A、B、C不在同一条直线上,因为所求的圆要经过A、B、C三点,所以圆心到这三点的距离相等,因此这个点要在线段AB的垂直的平分线上,又要在线段BC的垂直的平分线上.
结论:不在同一条直线上的三点确定一个圆.
·
C
O
A
B
l1
l2
3.以点O为圆心,OA(或OB、OC)为半径作圆,便可以作出经过A、B、C的圆.
1.分别连接AB、BC、AC;
2. 分别作出线段AB的垂直平分线l1和l2,设他们的交点为O ,则OA=OB=OC;
由于过A、B、C三点的圆的圆心只能是点O,半径等于OA,所以这样的圆只能有一个,即
提问:不在同一直线上四个点一定确定一个圆吗?
不在同一条直线上的三点确定一个圆-------------简单应用 (见学案)
2.三角形的外心(外接圆的心)是三角形三条边垂直平分线的交点。
C
O
A
B
1.经过三角形的三个顶点可以做一个圆
这个圆叫做三角形的外接圆
圆和三角形的位置关系:
这个三角形叫做这个圆的内接三角形。
结论(1)任意一个三角形的都有且只有一个外接圆
( 2)一个圆有无数个内接三角形
探究:活动三
1.锐角三角形的外心位置
2.直角三角形的外心位置
3.钝角三角形的外心位置
(见学案)
锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.
三角形外心位置特点:
本节课的收获:
1.设⊙O的半径为r,点P到圆心的距离OP = d,则有:
位置关系 大小关系
2.理解不在同一直线上的三个点确定一个圆并掌握它的运用.
(要求理解掌握上述知识)
3.了解三角形的外接圆和三角形外心的概念及不同的三角形外心的位置。
经过同一条直线三个点能作出一个圆吗?
活 动 四
提示:当直接证困难时,我们用反证法证明
所谓反证法,就是首先提出一个与
原命题结论相反的假设,然后从假
设出发,经过正确的推理,导出矛盾,
从而否定假设,进而肯定原命题的
一种方法.导出的矛盾主要有:与
已知条件矛盾;与已知的公理、定
理、定义、公式矛盾;与
反证法的三个步骤:
1、提出与原命题结论相反的假设
2、由假设出发,推出与已知条件或学过定理 的矛盾
3、由矛盾判定假设不成立,肯定结论正确
同课章节目录
