高中数学选修3-1第一讲 两河流域的数学(共27张PPT)
文档属性
| 名称 | 高中数学选修3-1第一讲 两河流域的数学(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-20 00:00:00 | ||
图片预览







文档简介
(共27张PPT)
第一讲 早期的算术与几何
—记数和测量
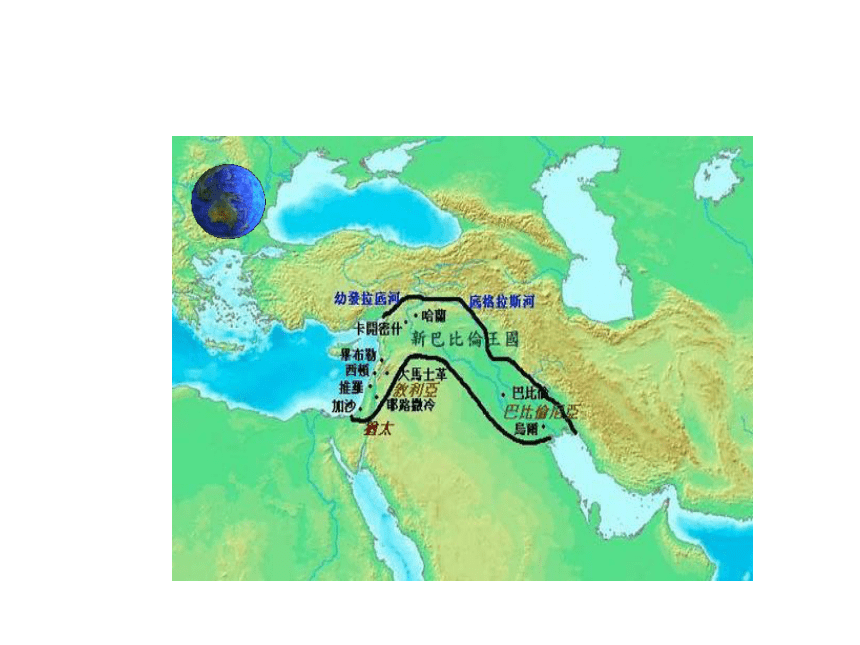
巴比伦古称“美索不达米亚” (底格里斯—幼发拉底河谷),意指两河之间地带.这是一块肥美的平原,环境优美,据传是《圣经》中伊甸园的原型.
公元前2000年左右建立的古巴比伦王国,首都巴比伦,是当时世界上最大的城市之一,最著名的“空中花园”被称为世界七大奇迹之一.可惜,后来因战争和生态环境的破坏,这座最美丽的城市于公元前539年被黄沙掩埋。巴比伦于约公元前64年被古罗马灭亡.
二、两河流域的数学
从公元前3000年到前2000年这一地区(在今伊拉克和伊朗西部)所创造的数学习惯统称为巴比伦数学.
公元前四、五千年,两河流域的苏美尔人用削尖的芦苇杆或木棒在软泥板上写字,泥板晒干后坚硬如石.由于这种文字形如楔子.所以称为楔形字.后来传给了巴比伦人.
楔形文字
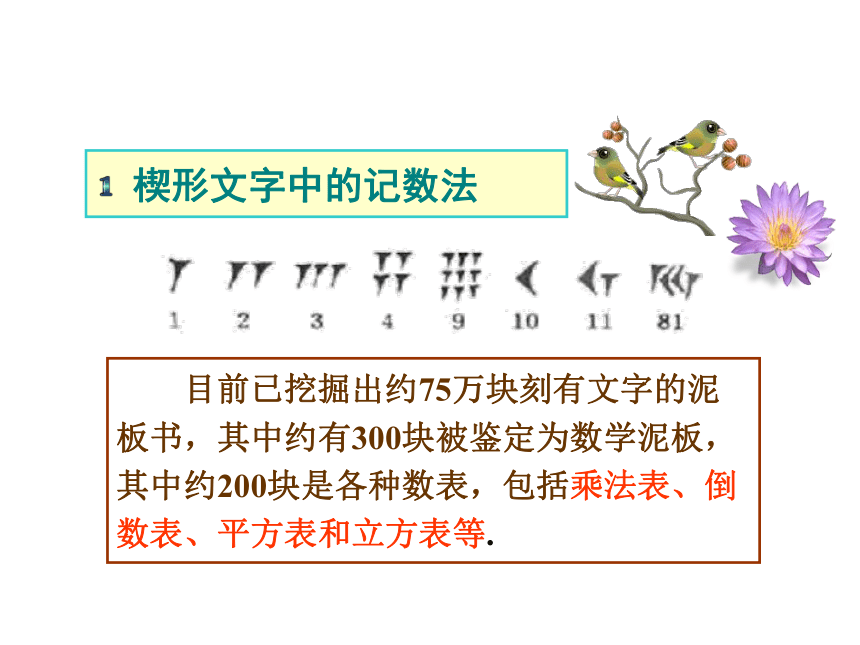
楔形文字中的记数法
目前已挖掘出约75万块刻有文字的泥板书,其中约有300块被鉴定为数学泥板,其中约200块是各种数表,包括乘法表、倒数表、平方表和立方表等.
带有四边形和数字符号30;1,24,51,10;42,25,35的泥版书.
这是世界上最古老的图书之一.
大约在公元前1800年—前1600年,巴比伦人发展成一套记数方法是10进制和60进制的混合物. 60以下用10进的简单累计制,60以上用60进的位值制.
巴比伦人在实践中已广泛引用了分数.而他们多令分母为常数并等于60.
如36=3×10﹢6,记为
泥板上的代数
巴比伦人已经由算术向代数过渡.他们的代数比几何先进得多.
许多泥板中载有一次和二次方程的问题,其中一元二次方程求根公式(只取正根)是世界上最早的求根公式.泥板上还有三次方程和含多个未知数的线性方程组的问题.
在哈莫拉比时代(公元前1792—前1600)的泥板上“两个正方形中,一个边长为另一个边长的 少10,两者面积只和为1000,求两个正方形的边长各是多少?”
这实际上是相当于解方程:
巴比伦已有数列概念.公元前300年左右的一块泥板上有相当于.
巴比伦人还知道相当于两数和的完全平方公式。
数列
泥板上的几何
的计算
有一块公元前1700年左右的圆饼状泥板上,刻有一个正方形并画出了对角线.对角线上写了行数字,即1,24,51,10,化成10进制小数就是
巴比伦人按勾股定理推算出来的单位正方形对角线的长,与真值的差不超过 比古印度的记载早一千多年,而误差小的多.
泥板上的几何图形
巴比伦人是最早发现“勾股定理”的.
勾股数
纽约哥伦比亚大学的珍本图书馆藏有一块年代为公元前1900—前1600的泥板,称为普林顿322号数学泥板.
根据记载,巴比伦人找到了不定方程 的整数解的一般表达式
这就是著名的毕达哥拉斯三元数组.早在公元前2000年就发现了.
巴比伦人知道三角形相似及对应边成比例关系,并且会计算简单面积和体积公式.
如圆的面积公式
其中c为圆周长由此推出
面积的计算
巴比伦人能正确计算长方形、梯形、三角形的面积.因水利工程等方面的需要他们得出计算堤坝的体积公式:
体积的计算
其中a、b为横截面梯形的上、下底,h
为堤坝的高,l为堤坝的长.
巴比伦人还能进行复杂的正四棱台体积和楔形平截头方锥的体积计算:
其中h为高, 为上、下底面积.
圆周度
巴比伦人将圆周分成360度,每度60分,每分60秒;一个小时也是60分钟,每分60秒.这就是今天度、分、秒制度的来历.
一星期有7天也是巴比伦建立而沿袭下来的制度.一年有12个月,每月有30天,每6年年末加上第13个月作为闰月.
两河流域的数学成就
在数学方面,巴比伦人已经知道如何度量矩形、直角三角形和等腰三角形的面积,以及圆柱体和平行六面体这类正多边体的体积.
他们对圆面积的度量比不上埃及人.
他们在计数上已经有了位置值的概念,但似乎没有表示零的方法.
古巴比伦的数学与古埃及的数学一样,主要解决各类具体问题的实用知识,处于原始算法积累时期.尽管古埃及的纸草书和巴比伦的泥板上都有求几何图形面积的问题,但本质上都是算术的应用,几何学作为独立的学科还不存在.
两河流域数学的局限
如图1-1是一个几何体的三视图(单位:cm)
(Ⅰ)画出这个几何体的直观图(不要求写画法);
(Ⅱ)求这个几何体的表面积及体积;
(Ⅲ)设异面直线 与 所成的角为 ,求
解:(Ⅰ)这个几何体的直观图如图1-2所示。
(Ⅱ)这个几何体是直三棱柱.
由于底面的高为1,所以
故所求全面积
这个几何体的体积
(Ⅲ)因为 ,所以 与 所成的角是 .在 ,
第一讲 早期的算术与几何
—记数和测量
巴比伦古称“美索不达米亚” (底格里斯—幼发拉底河谷),意指两河之间地带.这是一块肥美的平原,环境优美,据传是《圣经》中伊甸园的原型.
公元前2000年左右建立的古巴比伦王国,首都巴比伦,是当时世界上最大的城市之一,最著名的“空中花园”被称为世界七大奇迹之一.可惜,后来因战争和生态环境的破坏,这座最美丽的城市于公元前539年被黄沙掩埋。巴比伦于约公元前64年被古罗马灭亡.
二、两河流域的数学
从公元前3000年到前2000年这一地区(在今伊拉克和伊朗西部)所创造的数学习惯统称为巴比伦数学.
公元前四、五千年,两河流域的苏美尔人用削尖的芦苇杆或木棒在软泥板上写字,泥板晒干后坚硬如石.由于这种文字形如楔子.所以称为楔形字.后来传给了巴比伦人.
楔形文字
楔形文字中的记数法
目前已挖掘出约75万块刻有文字的泥板书,其中约有300块被鉴定为数学泥板,其中约200块是各种数表,包括乘法表、倒数表、平方表和立方表等.
带有四边形和数字符号30;1,24,51,10;42,25,35的泥版书.
这是世界上最古老的图书之一.
大约在公元前1800年—前1600年,巴比伦人发展成一套记数方法是10进制和60进制的混合物. 60以下用10进的简单累计制,60以上用60进的位值制.
巴比伦人在实践中已广泛引用了分数.而他们多令分母为常数并等于60.
如36=3×10﹢6,记为
泥板上的代数
巴比伦人已经由算术向代数过渡.他们的代数比几何先进得多.
许多泥板中载有一次和二次方程的问题,其中一元二次方程求根公式(只取正根)是世界上最早的求根公式.泥板上还有三次方程和含多个未知数的线性方程组的问题.
在哈莫拉比时代(公元前1792—前1600)的泥板上“两个正方形中,一个边长为另一个边长的 少10,两者面积只和为1000,求两个正方形的边长各是多少?”
这实际上是相当于解方程:
巴比伦已有数列概念.公元前300年左右的一块泥板上有相当于.
巴比伦人还知道相当于两数和的完全平方公式。
数列
泥板上的几何
的计算
有一块公元前1700年左右的圆饼状泥板上,刻有一个正方形并画出了对角线.对角线上写了行数字,即1,24,51,10,化成10进制小数就是
巴比伦人按勾股定理推算出来的单位正方形对角线的长,与真值的差不超过 比古印度的记载早一千多年,而误差小的多.
泥板上的几何图形
巴比伦人是最早发现“勾股定理”的.
勾股数
纽约哥伦比亚大学的珍本图书馆藏有一块年代为公元前1900—前1600的泥板,称为普林顿322号数学泥板.
根据记载,巴比伦人找到了不定方程 的整数解的一般表达式
这就是著名的毕达哥拉斯三元数组.早在公元前2000年就发现了.
巴比伦人知道三角形相似及对应边成比例关系,并且会计算简单面积和体积公式.
如圆的面积公式
其中c为圆周长由此推出
面积的计算
巴比伦人能正确计算长方形、梯形、三角形的面积.因水利工程等方面的需要他们得出计算堤坝的体积公式:
体积的计算
其中a、b为横截面梯形的上、下底,h
为堤坝的高,l为堤坝的长.
巴比伦人还能进行复杂的正四棱台体积和楔形平截头方锥的体积计算:
其中h为高, 为上、下底面积.
圆周度
巴比伦人将圆周分成360度,每度60分,每分60秒;一个小时也是60分钟,每分60秒.这就是今天度、分、秒制度的来历.
一星期有7天也是巴比伦建立而沿袭下来的制度.一年有12个月,每月有30天,每6年年末加上第13个月作为闰月.
两河流域的数学成就
在数学方面,巴比伦人已经知道如何度量矩形、直角三角形和等腰三角形的面积,以及圆柱体和平行六面体这类正多边体的体积.
他们对圆面积的度量比不上埃及人.
他们在计数上已经有了位置值的概念,但似乎没有表示零的方法.
古巴比伦的数学与古埃及的数学一样,主要解决各类具体问题的实用知识,处于原始算法积累时期.尽管古埃及的纸草书和巴比伦的泥板上都有求几何图形面积的问题,但本质上都是算术的应用,几何学作为独立的学科还不存在.
两河流域数学的局限
如图1-1是一个几何体的三视图(单位:cm)
(Ⅰ)画出这个几何体的直观图(不要求写画法);
(Ⅱ)求这个几何体的表面积及体积;
(Ⅲ)设异面直线 与 所成的角为 ,求
解:(Ⅰ)这个几何体的直观图如图1-2所示。
(Ⅱ)这个几何体是直三棱柱.
由于底面的高为1,所以
故所求全面积
这个几何体的体积
(Ⅲ)因为 ,所以 与 所成的角是 .在 ,
同课章节目录
- 第一讲 早期的算术与几何
- 一 古埃及的数学
- 二 两河流域的数学
- 三 丰富多彩的记数制度
- 第二讲 古希腊数学
- 一 希腊数学的先行者
- 二 毕达哥拉斯学派
- 三 欧几里得与《原本》
- 四 数学之神──阿基米德
- 第三讲 中国古代数学瑰宝
- 一 《周髀算经》与赵爽弦图
- 二 《九章算术》
- 三 大衍求一术
- 四 中国古代数学家
- 第四讲 平面解析几何的产生
- 一 坐标思想的早期萌芽
- 二 笛卡儿坐标系
- 三 费马的解析几何思想
- 四 解析几何的进一步发展
- 第五讲 微积分的诞生
- 一 微积分产生的历史背景
- 二 科学巨人牛顿的工作
- 三 莱布尼茨的“微积分”
- 第六讲 近代数学两巨星
- 一 分析的化身──欧拉
- 二 数学王子──高斯
- 第七讲 千古谜题
- 一 三次、四次方程求根公式的发现
- 二 高次方程可解性问题的解决
- 三 伽罗瓦与群论
- 四 古希腊三大几何问题的解决
- 第八讲 对无穷的深入思考
- 一 古代的无穷观念
- 二 无穷集合论的创立
- 三 集合论的进一步发展与完善
- 第九讲 中国现代数学的开拓与发展
- 一 中国现代数学发展概观
- 二 人民的数学家──华罗庚
- 三 当代几何大师──陈省身
