2020人教版高中物理必修二5.4圆周运动
文档属性
| 名称 | 2020人教版高中物理必修二5.4圆周运动 |

|
|
| 格式 | zip | ||
| 文件大小 | 361.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-02-20 00:21:55 | ||
图片预览




文档简介
第八讲:匀速圆周运动
【学习目标】
理解圆周运动的线速度、角速度和周期
掌握圆周运动的特点
掌握角速度和线速度的关系和应用
【学习过程】
知识点一、线速度
1.圆周运动.
物体沿着________的运动称为圆周运动.圆周运动的轨迹为一圆弧,故圆周运动为曲线运动,所以一定是______运动.
2.线速度的概念.
做圆周运动的物体,通过的弧长与所用时间的______叫做线速度.
3.线速度的特点.
(1)意义.
线速度是描述物体做圆周运动________的物理量,其物理意义与瞬时速度的相同.
(2)大小.
线速度的大小用公式v=________来计算,Δs是在时间Δt内通过的弧长,线速度的单位是________.
(3)方向.
线速度是矢量,线速度的方向就是圆周上该点的________.
4.匀速圆周运动.
(1)定义.
如果物体沿着圆周运动,并且_____________处处相等,这种运动叫做匀速圆周运动.
(2)运动性质.
由于匀速圆周运动的线速度方向时刻都在改变,所以匀速圆周运动是一种________运动.
考点二、角速度、周期(频率)
1.角速度.
(1)定义:在匀速圆周运动中,连接物体与圆心的半径所转过的________与所用________的比值.
(2)物理含义:描述质点转过________的快慢.
(3)大小:ω=,单位:______(rad/s或rad·s-1).
(4)匀速圆周运动是角速度________的运动.
2.周期和频率.
(1)周期:做圆周运动的物体运动________所用的时间.
(2)频率:做圆周运动的物体在1秒钟内运动的________.
(3)频率与周期的关系:f=________.
3.转速.
物体单位时间内转过的________.通常用n表示.单位:转每秒(r/s)
4.线速度、角速度和周期的关系.
(1)线速度和周期的关系:v=________.
(2)角速度和周期的关系:ω=________.
(3)线速度和角速度的关系:v=________.
(4)转速与角速度关系:n= .
【问题探究】
问题一、比较线速度和角速度
v、ω、r中有一个不变时,其他两个变量的变化关系:
(1)当r一定时,v∝ω.如转动飞轮边缘质点的运动,当飞轮转速n增大时,角速度ω=2πn也增大,故线速度v=ωr也相应增大,反之亦然.
(2)当ω一定时,v∝r.如地球自转时,不同纬度的地面质点做圆周运动的半径不同,但地面各质点随地球自转的角速度ω均相等,则线速度大小不等.质点做圆周运动所在圆的半径越大,线速度也越大.反之亦然.
(3)当v一定时,ω∝.如皮带传动装置中,两轮边缘质点线速度大小相同,则大轮的角速度小,而小轮的角速度大.
名师提示:线速度和角速度都是描述物体做匀速圆周运动快慢的物理量,线速度侧重于描述物体通过弧长快慢的程度,而角速度侧重于描述物体转过圆心角的快慢程度.它们都有一定的局限性,其中任何一个物理量(v或ω)都无法全面准确地反映做匀速圆周运动的物体的运动状态.
【针对训练】
1.关于匀速圆周运动,下列说法不正确的是( )
A.匀速圆周运动是变速运动
B.匀速圆周运动的速率不变
C.任意相等时间内通过的位移相等
D.任意相等时间内通过的路程相等
答案:C
2.[多选](2016·宜兴月考)质点做匀速圆周运动时,下列说法中正确的是( )
A.因为v=ωR,所以线速度v与轨道半径R成正比
B.因为ω=,所以角速度ω与轨道半径R成反比
C.因为ω=2πn,所以角速度ω与转速n成正比
D.因为ω=,所以角速度ω与周期T成反比
解析:选CD ω一定时,线速度v与轨道半径R成正比,A错误;v一定时,角速度ω与轨道半径R成反比,B错误;在用转速或周期表示角速度时,角速度与转速成正比,与周期成反比,C、D正确。
问题二、传动问题中v、ω、T与r的关系是怎样的?
1.同轴传动.
如图所示,A点和B点在同轴的一个“圆盘”上,所以角速度相同.但因A、B两点与轴的距离不同,即转动半径不同,所以线速度不同,设半径分别为r和R,且r
2.皮带传动.
如图所示,A点和B点分别是两个轮子边缘上的点,两个轮子用皮带连起来,并且皮带不打滑,所以它们的线速度必然相同,但是因为半径不同,所以角速度不同.线速度、角速度、周期之间存在的定量关系为:vA=vB,=,=.
3.齿轮传动.
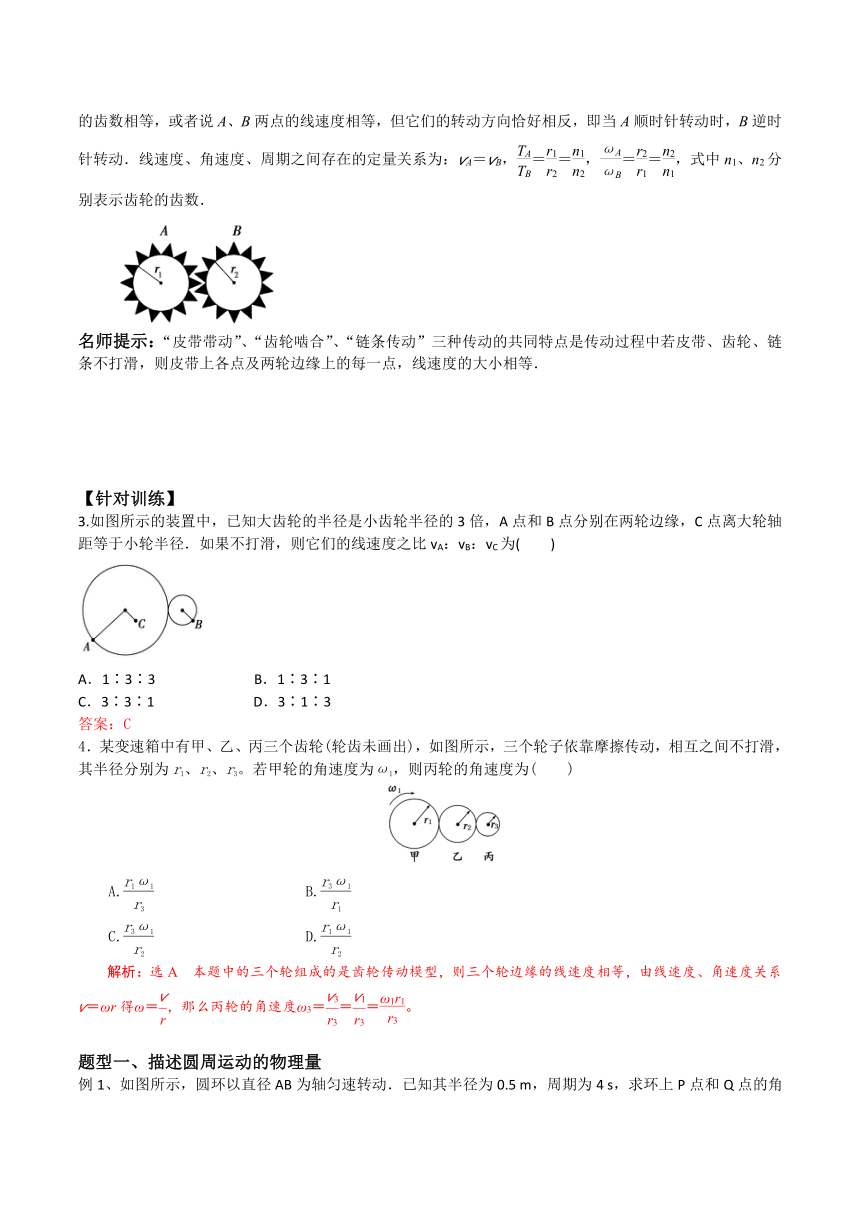
如图所示,A点和B点分别是两个齿轮边缘上的点,两个齿轮轮齿啮合.两个轮子在同一时间内转过的齿数相等,或者说A、B两点的线速度相等,但它们的转动方向恰好相反,即当A顺时针转动时,B逆时针转动.线速度、角速度、周期之间存在的定量关系为:vA=vB,==,==,式中n1、n2分别表示齿轮的齿数.
名师提示:“皮带带动”、“齿轮啮合”、“链条传动”三种传动的共同特点是传动过程中若皮带、齿轮、链条不打滑,则皮带上各点及两轮边缘上的每一点,线速度的大小相等.
【针对训练】
3.如图所示的装置中,已知大齿轮的半径是小齿轮半径的3倍,A点和B点分别在两轮边缘,C点离大轮轴距等于小轮半径.如果不打滑,则它们的线速度之比vA:vB:vC为( )
A.1∶3∶3 B.1∶3∶1
C.3∶3∶1 D.3∶1∶3
答案:C
4.某变速箱中有甲、乙、丙三个齿轮(轮齿未画出),如图所示,三个轮子依靠摩擦传动,相互之间不打滑,其半径分别为r1、r2、r3。若甲轮的角速度为ω1,则丙轮的角速度为( )
A. B.
C. D.
解析:选A 本题中的三个轮组成的是齿轮传动模型,则三个轮边缘的线速度相等,由线速度、角速度关系v=ωr得ω=,那么丙轮的角速度ω3===。
题型一、描述圆周运动的物理量
例1、如图所示,圆环以直径AB为轴匀速转动.已知其半径为0.5 m,周期为4 s,求环上P点和Q点的角速度和线速度.
解析:P点和Q点的角速度相同,ω=≈1.57 rad/s.P点和Q点绕AB轴做圆周运动,其轨迹的圆心不同,P点和Q点的圆半径分别为rP=R·sin 30°=R,rQ=R·sin 60°=R.故其线速度分别为vP=ωrP≈0.39 m/s,vQ=ωrQ≈0.68 m/s.
变式练习 1.(多选)质点做匀速圆周运动,则( )
A.在任何相等的时间里,质点的位移都相等
B.在任何相等的时间里,质点通过的路程都相等
C.在任何相等的时间里,质点运动的平均速度都相同
D.在任何相等的时间里,连接质点和圆心的半径转过的角度都相等
答案:BD
题型二、传动装置中各物理量间的关系
例2、如右图所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三轮半径的关系是rA=rC=2rB.若皮带不打滑,求A、B、C三轮边缘的a、b、c三点的角速度之比和线速度之比.
答案:A、B两轮通过皮带传动,皮带不打滑,则A、B两轮边缘上各点的线速度大小相等,即
va=vb或vavb=1:1①
由v=ωr得ωaωb=rBrA=1:2②
B、C两轮固定在一起绕同一轴转动,则B、C两轮上各点的角速度相同,即
ωb=ωc或ωb ωc=1:1③
由v=ωr得vbvc=rBrC=1:2④
由②③两式得ωaωbωc=1:2:2
由①④两式得vavbvc=1:1:2
ωaωbωc=1:2:2 vavbvc=1:1:2
变式练习2.如图所示皮带传动装置,皮带轮O1和O2上的三点A、B和C,O1A=O2C=r,O2B=2r,则皮带轮转动时(皮带传动时不打滑),关于A、B、C三质点的运动情况是( )
A.vA=vB,vB>vC B.ωA=ωB,vB>vC
C.vA=vB,ωB>ωC D.ωC<ωB,vB>vC
答案:A
名师归纳:解决这类问题时要注意抓住传动装置的特点:同轴转动时两轮的角速度相等,皮带传动(不打滑)时两轮边缘的线速度大小相等,求解时注意运用v=ωr找出联系
题型三、与其他运动相结合
例3 、如右图所示,直径为d的纸制圆筒以角速度ω绕垂直纸面的轴O匀速转动(图示为截面).从枪口发射的子弹沿直径穿过圆筒.若子弹在圆筒旋转不到半周时,在圆周上留下a、b两个弹孔.已知aO与bO夹角为θ,求子弹的速度.
解析:设子弹速度为v,则子弹穿过圆筒的时间t=.此时间内圆筒转过的角度α=π-θ.据α=ωt,得π-θ=ω.则子弹的速度v=.
变式练习3.如右图所示,B物体放在光滑的水平地面上,在水平力F的作用下由静止开始运动,B物体质量为m,同时A物体在竖直面内由M点开始做半径为r、角速度为ω的匀速圆周运动.则力F多大可使A和B两物体的速度相同?
解析:因为物体B在力F作用下沿水平面向右做匀加速运动,速度方向水平向右,要使A与B速度相同,则只有当A运动到圆轨道的最低点时,才有可能.设A、B运动时间t后两者速度相同(大小相等、方向相同).对B有:F=ma,a=,vB=at=t,对A有:t=T+nT=(n+)·(n=0,1,2,…),vA=ωr,令vA=vB,得(n+)·=ωr(n=0,1,2,…),解得F=(n=0,1,2,…).
名师归纳:有些题目会涉及圆周运动、直线运动和平抛运动等不同的运动,不同运动规律在解决同一问题时,必然有一个物理量起桥梁作用,将两种不同运动联系起来,这一物理量常常是“时间”.通常会涉及由圆周运动引起的多解问题.
课堂练习
1.(多选)关于匀速圆周运动,下列说法正确的是( )
A.匀速圆周运动是匀速运动
B.匀速圆周运动是变速运动
C.匀速圆周运动是线速度不变的运动
D.匀速圆周运动是线速度大小不变的运动
答案:BD
2.关于做匀速圆周运动物体的线速度、角速度、周期之间的关系,下列说法正确的是( )
A.线速度大的角速度一定大
B.线速度大的周期一定小
C.角速度大的半径一定小
D.角速度大的周期一定小
答案:D
3.关于匀速圆周运动的线速度v、角速度ω和半径r,下列说法正确的是( )
A.若r一定,则v与ω成正比
B.若r一定,则v与ω成反比
C.若ω一定,则v与r成反比
D.若v一定,则ω与r成正比[
解析:根据v=ωr知,若r一定,则v与ω成正比;若ω一定,则v与r成正比;若v一定,则ω与r成反比.只有选项A正确.
答案:A
4.甲沿着半径为R的圆周跑道匀速跑步,乙沿着半径为2R的圆周跑道匀速跑步,在相同的时间内,甲、乙各自跑了一圈,他们的角速度和线速度的大小分别为ω1、ω2和v1、v2,则( )
A.ω1>ω2,v1>v2
B.ω1<ω2,v1
解析:由于甲、乙在相同时间内各自跑了一圈,v1=,v2=,v1
5.在一棵大树将要被伐倒的时候,有经验的伐木工人就会双眼紧盯着地梢,根据树梢的运动情况就能判断大树正在朝着哪个方向倒下,从而避免被倒下的大树砸伤,从物理知识的角度来解释,以下说法正确的是( )
A.树木倒下时,树梢的角速度较大,易于判断
B.树木倒下时,树梢的线速度较大,易于判断
C.树木倒下时,树梢的周期较大,易于判断
D.伐木工人的经验没有科学依据
解析:整个大树的角速度和周期相同,是树梢的线速度大.
答案:B
6.两个小球固定在一根长为L的杆的两端,绕杆上的O点做圆周运动,如图所示,当小球1的速度为v1时,小球2的速度为v2,则转轴O到小球2的距离为( )
A. B.
C. D.
解析:设小球1、2做圆周运动的半径分别为r1、r2,则v1∶v2=ωr1∶ωr2=r1∶r2,又因r1+r2=L,所以小球2到转轴O的距离r2=,B正确.
答案:B
7.(多选)对于做匀速圆周运动的物体,下面说法正确的是( )
A.相等时间里线速度的变化相等
B.相等的时间里通过的弧长相等[来
C.相等的时间里发生的位移相等
D.相等的时间里转过的角度相等学
解析:匀速圆周运动的线速度变化大小处处相等,但方向不同,A错;根据v=可知Δs=v·Δt,相等时间内通过的弧长相等,进一步分析可知,相等时间内通过的路程等于弧长,即也相等,相等时间内通过的位移大小等于相应的弦长,大小相等,但方向不同,B正确,C错误.根据ω=可知Δθ=ω·Δt,D正确.
答案:BD[科§网Z§X§X§K]:Z.xx.k.Com]Z。xx。
8.(多选)关于质点做圆周运动,下列说法正确的是( )
A.半径一定,角速度大小和线速度大小成反比
B.半径一定,线速度大小和角速度大小成正比
C.线速度大小一定,角速度大小与半径成反比
D.角速度一定,线速度大小与半径成反比
解析:由表达式v=ωr可知,B、C是正确.
答案:BC
9.(多选)一般转动机械上都标有“×××r/min”,该数值是转动机械正常工作时的转速,不同的转动机械上标有的转速一般是不同的.下列有关转速的说法正确的是( )
A.转速越大,说明该转动机械正常工作时的线速度一定越大
B.转速越大,说明该转动机械正常工作时的角速度一定越大
C.转速越大,说明该转动机械正常工作时的周期一定越大
D.转速越大,说明该转动机械正常工作时的周期一定越小
答案:BD
10.(多选)一辆卡车在水平路面上行驶,已知该车轮胎半径为R,轮胎转动的角速度为ω,关于各点的线速度大小下列说法正确的是( )
A.相对于地面,轮胎与地面的接触点的速度为ωR
B.相对于地面,车轴的速度大小为ωR
C.相对于地面,轮胎上缘的速度大小为ωR
D.相对于地面,轮胎上缘的速度大小为2ωR
解析:因为轮胎不打滑,相对于地面,轮胎与地面接触处保持相对静止,该点相当于转动轴,它的速度为零,车轴的速度为ωR.而轮胎上缘的速度大小为2ωR.故选项B、D正确.
答案:BD
11.(多选)自行车的传动装置如图所示,A、B、C分别为大齿轮、小齿轮、后轮边缘上的一点,则在此传动装置中( )
A.B、C两点的线速度大小相等
B.A、B两点的线速度大小相等
C.A、B两点的角速度与对应的半径成正比
D.B、C两点的线速度与对应的半径成正比
解析:大齿轮与小齿轮间是皮带传动,A、B两点的线速度相同,角速度与对应的半径成反比,B正确、C错误.小齿轮与后轮是同轴转动,B、C两点的角速度相同,线速度与对应的半径成正比,A错误、D正确.
答案:BD
12.机械手表的分针与秒针从第一次重合至第二次重合,中间经历的时间为( )
A. min B.1 min
C. min D. min
答案:C
13.如图所示,在男女双人花样滑冰运动中,男运动员以自己为转动轴拉着女运动员做匀速圆周运动。若男运动员的转速为30 r/min,女运动员触地冰鞋的线速度为4.7 m/s,求:
(1)女运动员做圆周运动的角速度;
(2)女运动员触地冰鞋做圆周运动的半径。
解析:男运动员与女运动员转速相同,即
n女=n男=0.5 r/s
(1)女运动员的角速度
ω=2πn女=2π×0.5 rad/s=3.14 rad/s
(2)由v=ωr得r== m≈1.5 m
答案:(1)3.14 rad/s (2)1.5 m
14.(2016·长治高一检测)如图所示,半径为R的圆盘绕垂直于盘面的中心轴匀速转动,在其正上方h处沿半径OB方向水平抛出一小球与圆盘只碰一次,且落点恰好为圆盘边缘上的B点,求小球的初速度v的大小及圆盘转动的角速度ω的大小(重力加速度为g)。
[解析] 小球做平抛运动,竖直方向有h=gt2,则运动时间t=
又因为其水平方向的位移为R,所以小球的初速度
v==R
设在时间t内,圆盘转过了n周,则转过的角度θ=n·2π(n=1,2,3,……)
又因为θ=ωt
故圆盘转动的角速度ω==2nπ(n=1,2,3,……)
[答案] R 2nπ(n=1,2,3,……)
