五年级下册数学一课一练-3.2长方体和正方体的表面积 人教新版 (含答案)
文档属性
| 名称 | 五年级下册数学一课一练-3.2长方体和正方体的表面积 人教新版 (含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 115.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-20 20:55:19 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级下册数学一课一练-3.2长方体和正方体的表面积
一、单选题
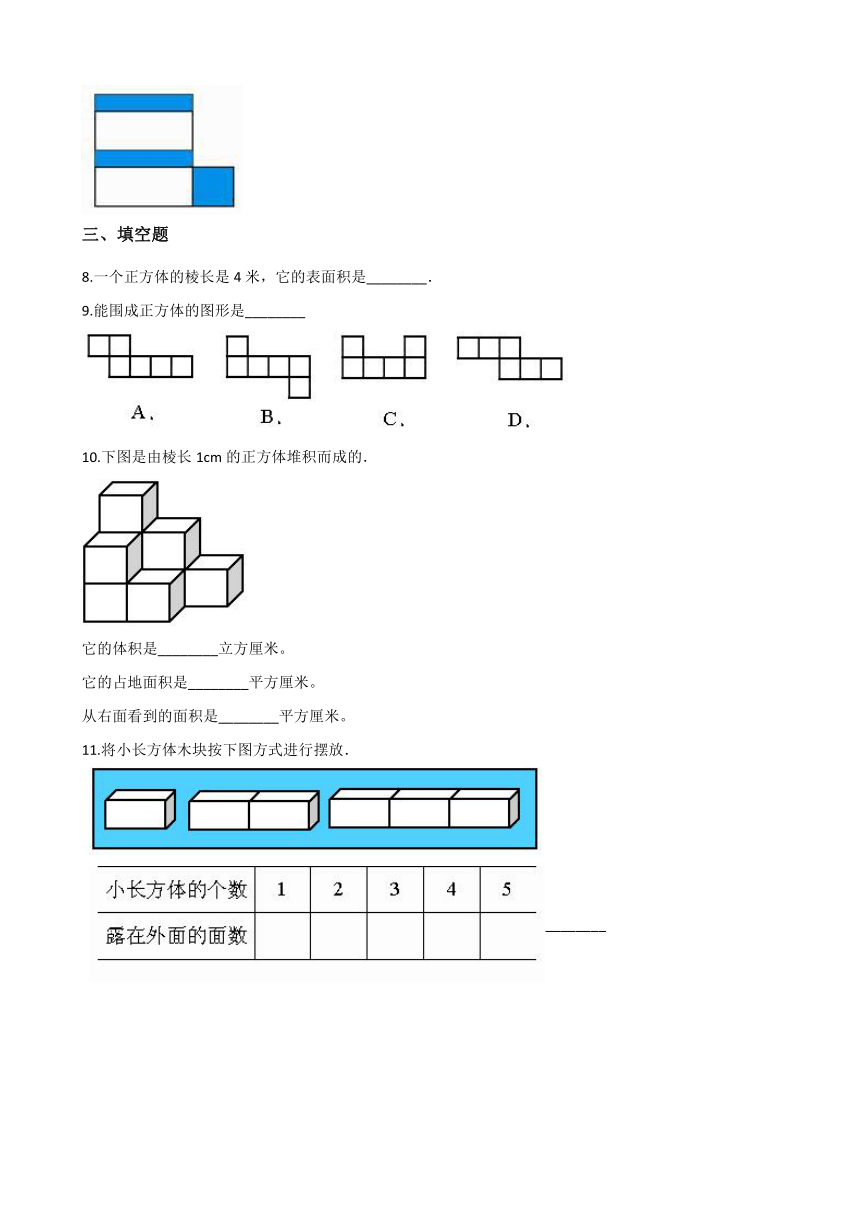
1.一个长方体水池,长20米,宽10米,深2米,占地(??? )平方米。
A.?400???????????????????????????????????????B.?200???????????????????????????????????????C.?520???????????????????????????????????????D.?40
2.如图,沿虚线把长方体木料刚好锯成2个同样的正方体,这样表面积比原长方体增加了32cm2。原来长方体木料的表面积是(??? )cm。
A.?64???????????????????????????????????????B.?128???????????????????????????????????????C.?160???????????????????????????????????????D.?320
3.下面四个图形中,经过折叠能围成如图只有三个面上印有图案的正方体纸盒的是(??? )
A.?????????????????????????????????????B.?
C.???????????????????????????????????????D.?
4.把一个长方体盒子的侧面展开,得到一张正方形的纸.那么,这个盒子的底面边长与高的比是(?? )
A.?1∶4?????????????????????????????????????????B.?4∶1?????????????????????????????????????????C.?1∶8
二、判断题
5.正方体的表面积=棱长×棱长×4。(??? )
6.长方体的展开图一定是由六个长方形组成的,不可能有正方形。
7.下面的展开图可以拼成一个长方体。
三、填空题
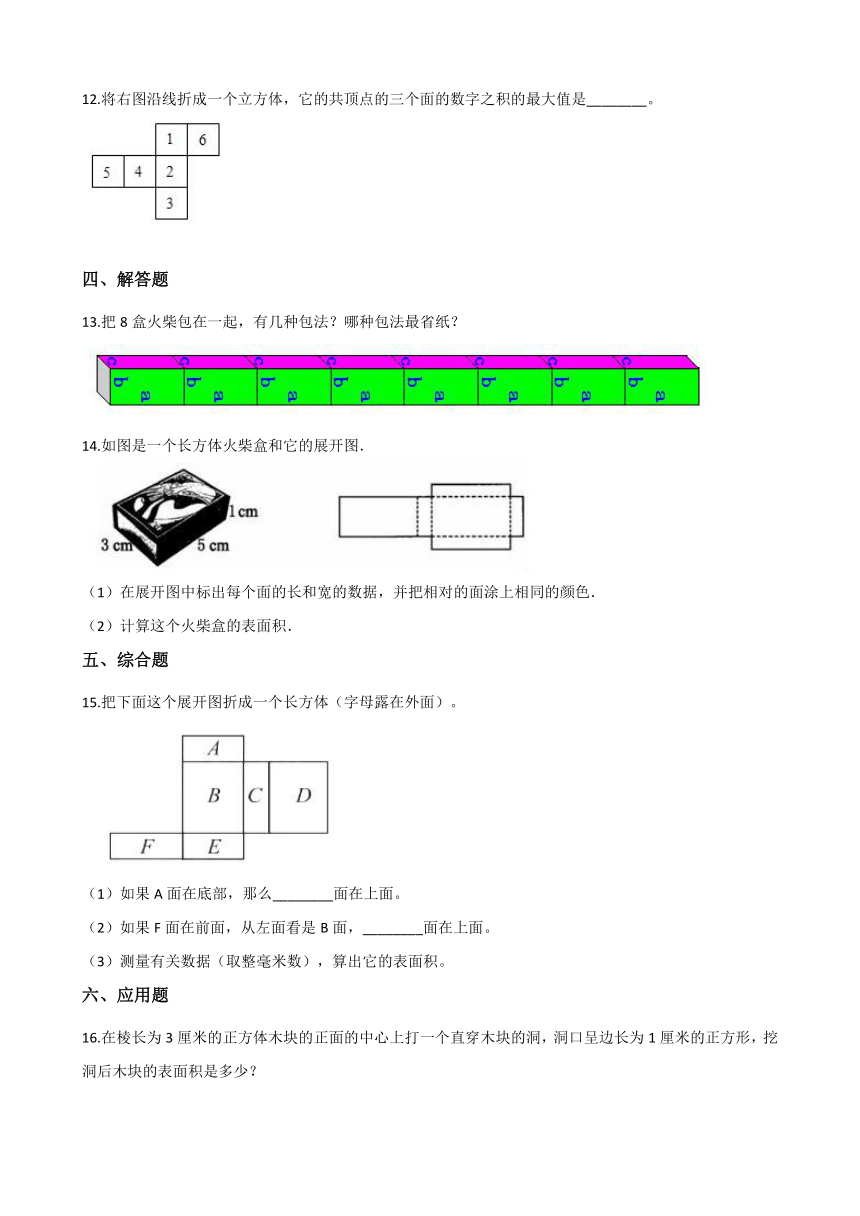
8.一个正方体的棱长是4米,它的表面积是________.
9.能围成正方体的图形是________
10.下图是由棱长1cm的正方体堆积而成的.
它的体积是________立方厘米。
它的占地面积是________平方厘米。
从右面看到的面积是________平方厘米。
11.将小长方体木块按下图方式进行摆放.
________
12.将右图沿线折成一个立方体,它的共顶点的三个面的数字之积的最大值是________。
四、解答题
13.把8盒火柴包在一起,有几种包法?哪种包法最省纸?
14.如图是一个长方体火柴盒和它的展开图.
(1)在展开图中标出每个面的长和宽的数据,并把相对的面涂上相同的颜色.
(2)计算这个火柴盒的表面积.
五、综合题
15.把下面这个展开图折成一个长方体(字母露在外面)。
(1)如果A面在底部,那么________面在上面。
(2)如果F面在前面,从左面看是B面,________面在上面。
(3)测量有关数据(取整毫米数),算出它的表面积。
六、应用题
16.在棱长为3厘米的正方体木块的正面的中心上打一个直穿木块的洞,洞口呈边长为1厘米的正方形,挖洞后木块的表面积是多少?
参考答案
一、单选题
1.【答案】 B
【解析】【解答】解:20×10=200(平方米)
故答案为:B。
【分析】占地面积就是底面积,也就是长20米,宽10米的长方形面积。
2.【答案】 C
【解析】【解答】32÷2=16(cm?)
16×6×2-32
=96×2-32
=192-32
=160(cm?)
故答案为:C
【分析】 沿虚线把长方体木料刚好锯成2个同样的正方体, 表面积比原长方体增加了32cm?。 这时增加了两个正方形的面,?这两个正方形的面积是32cm?。求出一个正方形的面积后,用“这个正方形的面积×6=一个正方体的表面积”,“这个正方体的表面积×2-32cm?=长方体的表面积”。
3.【答案】 B
【解析】【解答】选项A,通过折叠,△和□会是相对的面,与原题不符;
选项B,通过观察分析,△、○和□是相邻的3个面中的图案,符合题意;
选项C,通过折叠,△和□会是相对的面,与原题不符;
选项D,通过折叠,△和○会是相对的面,与原题不符.
故答案为:B.
【分析】观察图可知,△、○和□是相邻的3个面中的图案,据此逐项分析,找出符合题意的图形.
4.【答案】 A
【解析】【解答】把一个长方体盒子的侧面展开,得到一张正方形的纸.那么,这个盒子的底面边长与高的比是1:4.
故答案为:A.
【分析】把一个长方体盒子的侧面展开,得到一张正方形的纸.因为正方形的边长相等,所以这个盒子的高是盒子底面边长的4倍,据此解答.
二、判断题
5.【答案】 错误
【解析】【解答】正方体的表面积=棱长×棱长×6
故答案:错误
【分析】正方体表面是由六个完全相同的正方形围成的,正方形的面积是边长×边长,边长就是正方体的棱长,所以 正方体的表面积应是:棱长×棱长×6
6.【答案】 错误
【解析】【解答】长方体的6个面在特殊情况下有可能有2个面是正方形。所以长方体的展开图也有可能有两个面是正方形。
故答案为:错误
【分析】6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形是长方体。
7.【答案】错误
【解析】【解答】展开图可以拼成一个长方体。说法错误。
故答案为:错误
【分析】长方体的展开图应是6个面,而这个图只有5个面,所以这个展开图不能拼成长方体。
三、填空题
8.【答案】 96平方米
【解析】【解答】4×4×6
=16×6
=96(平方米)
故答案为:96平方米.
【分析】已知正方体的棱长,求正方体的表面积,用公式:正方体的表面积=棱长×棱长×6,据此列式解答.
9.【答案】 BD
【解析】【解答】解:A、折起后有重叠的面,不能围成正方体;
B、折起后没有重叠的面,能围成正方体;
C、折起后有重叠的面,不能围成正方体;
D、折起后没有重叠的面,能围成正方体.
故答案为:BD
【分析】把其中一个面作为底面,然后确定另外的面,如果另外的面不重叠就能折成正方体,如果重叠就不能折成正方体.
10.【答案】9;5;5
【解析】【解答】1个正方体的体积是1×1×1=1(立方厘米),1+3+5=9(个),一共9个正方体,体积是9立方厘米;
1个正方体的一个面的面积是1×1=1(平方厘米),底面一共5个面,它的占地面积是5平方厘米;
从右面能看到5个面,看到的面积是5平方厘米。
故答案为:9;5;5 。
【分析】棱长×棱长×棱长=体积;棱长×棱长=面积。
11.【答案】 5;8;11;14;17
【解析】【解答】解:填表如下:
故答案为:5;8;11;14;17。
【分析】下面没有露在外面,所以第一个长方体有5个面露在外面;每增加一个长方体露在外面的面就会增加3个,按照规律计算露在外面的面的个数即可。
12.【答案】 90
【解析】【解答】解:折成的正方体如图:
折成后的立方体的上面、前面和右面上的数字分别是5,3,6,它们的积最大,5×3×6=90
故答案为:90
【分析】把2作为底面,4、6就是左右面,5是上面,3是前面,1是后面,然后确定公顶点的三个数字最大是多少,再求出乘积即可.
四、解答题
13.【答案】 解:
最大面重合的包装方法最省纸.
【解析】【解答】根据排列层数及重合面的不同,有 :
包装法。? 最大面重合的包装方法最省纸.
【分析】本题考查逆向思维问题的能力。
14.【答案】 (1)
(2)(3×5+3×1+1×5)×2
=23×2
=46(平方厘米)
答: 这个火柴盒的表面积是46平方厘米。
【解析】【分析】(1)标数据时可以根据数量的大小和展开图综合判断;
(2)长方体表面积=(长×宽+长×高+宽×高)×2.
五、综合题
15.【答案】 (1)E
(2)E
(3)经过测量,这个长方体的长是30毫米,宽是20毫米,高是10毫米,
(30×20+20×10+30×10)×2=2200(平方毫米)
答:这个长方体的表面积是2200平方毫米。
【解析】【解答】解:(1)如果A面在底部,那么E面在上面;
(2)如果F面在前面,从左面看是B面,E面在上面;
【分析】(1)从图中可以看出,A的相对面是E,所以如果A面在底部,那么E面在上面;
(2)如果F面在前面,从左面看是B面,与B面和F面连接的两个面分别是E面和D面,根据F面和B面的位置可以得出E面在上面;
(3)量出长方体的长、宽、高的长度,长方体的表面积=(长×宽+长×高+宽 ×高)×2,然后代入数据作答即可。
六、应用题
16.【答案】 解:3×3×6﹣1×1×2+1×3×4
=54﹣2+12
=64(平方厘米)
答:挖洞后的木块的表面积是64平方厘米.
【解析】【分析】根据题干,挖洞后的木块的表面积在减少2个1×1面的同时,增加了4个1×3的面的面积,据此计算即可解答问题.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级下册数学一课一练-3.2长方体和正方体的表面积
一、单选题
1.一个长方体水池,长20米,宽10米,深2米,占地(??? )平方米。
A.?400???????????????????????????????????????B.?200???????????????????????????????????????C.?520???????????????????????????????????????D.?40
2.如图,沿虚线把长方体木料刚好锯成2个同样的正方体,这样表面积比原长方体增加了32cm2。原来长方体木料的表面积是(??? )cm。
A.?64???????????????????????????????????????B.?128???????????????????????????????????????C.?160???????????????????????????????????????D.?320
3.下面四个图形中,经过折叠能围成如图只有三个面上印有图案的正方体纸盒的是(??? )
A.?????????????????????????????????????B.?
C.???????????????????????????????????????D.?
4.把一个长方体盒子的侧面展开,得到一张正方形的纸.那么,这个盒子的底面边长与高的比是(?? )
A.?1∶4?????????????????????????????????????????B.?4∶1?????????????????????????????????????????C.?1∶8
二、判断题
5.正方体的表面积=棱长×棱长×4。(??? )
6.长方体的展开图一定是由六个长方形组成的,不可能有正方形。
7.下面的展开图可以拼成一个长方体。
三、填空题
8.一个正方体的棱长是4米,它的表面积是________.
9.能围成正方体的图形是________
10.下图是由棱长1cm的正方体堆积而成的.
它的体积是________立方厘米。
它的占地面积是________平方厘米。
从右面看到的面积是________平方厘米。
11.将小长方体木块按下图方式进行摆放.
________
12.将右图沿线折成一个立方体,它的共顶点的三个面的数字之积的最大值是________。
四、解答题
13.把8盒火柴包在一起,有几种包法?哪种包法最省纸?
14.如图是一个长方体火柴盒和它的展开图.
(1)在展开图中标出每个面的长和宽的数据,并把相对的面涂上相同的颜色.
(2)计算这个火柴盒的表面积.
五、综合题
15.把下面这个展开图折成一个长方体(字母露在外面)。
(1)如果A面在底部,那么________面在上面。
(2)如果F面在前面,从左面看是B面,________面在上面。
(3)测量有关数据(取整毫米数),算出它的表面积。
六、应用题
16.在棱长为3厘米的正方体木块的正面的中心上打一个直穿木块的洞,洞口呈边长为1厘米的正方形,挖洞后木块的表面积是多少?
参考答案
一、单选题
1.【答案】 B
【解析】【解答】解:20×10=200(平方米)
故答案为:B。
【分析】占地面积就是底面积,也就是长20米,宽10米的长方形面积。
2.【答案】 C
【解析】【解答】32÷2=16(cm?)
16×6×2-32
=96×2-32
=192-32
=160(cm?)
故答案为:C
【分析】 沿虚线把长方体木料刚好锯成2个同样的正方体, 表面积比原长方体增加了32cm?。 这时增加了两个正方形的面,?这两个正方形的面积是32cm?。求出一个正方形的面积后,用“这个正方形的面积×6=一个正方体的表面积”,“这个正方体的表面积×2-32cm?=长方体的表面积”。
3.【答案】 B
【解析】【解答】选项A,通过折叠,△和□会是相对的面,与原题不符;
选项B,通过观察分析,△、○和□是相邻的3个面中的图案,符合题意;
选项C,通过折叠,△和□会是相对的面,与原题不符;
选项D,通过折叠,△和○会是相对的面,与原题不符.
故答案为:B.
【分析】观察图可知,△、○和□是相邻的3个面中的图案,据此逐项分析,找出符合题意的图形.
4.【答案】 A
【解析】【解答】把一个长方体盒子的侧面展开,得到一张正方形的纸.那么,这个盒子的底面边长与高的比是1:4.
故答案为:A.
【分析】把一个长方体盒子的侧面展开,得到一张正方形的纸.因为正方形的边长相等,所以这个盒子的高是盒子底面边长的4倍,据此解答.
二、判断题
5.【答案】 错误
【解析】【解答】正方体的表面积=棱长×棱长×6
故答案:错误
【分析】正方体表面是由六个完全相同的正方形围成的,正方形的面积是边长×边长,边长就是正方体的棱长,所以 正方体的表面积应是:棱长×棱长×6
6.【答案】 错误
【解析】【解答】长方体的6个面在特殊情况下有可能有2个面是正方形。所以长方体的展开图也有可能有两个面是正方形。
故答案为:错误
【分析】6个长方形(特殊情况有两个相对的面是正方形)围成的立体图形是长方体。
7.【答案】错误
【解析】【解答】展开图可以拼成一个长方体。说法错误。
故答案为:错误
【分析】长方体的展开图应是6个面,而这个图只有5个面,所以这个展开图不能拼成长方体。
三、填空题
8.【答案】 96平方米
【解析】【解答】4×4×6
=16×6
=96(平方米)
故答案为:96平方米.
【分析】已知正方体的棱长,求正方体的表面积,用公式:正方体的表面积=棱长×棱长×6,据此列式解答.
9.【答案】 BD
【解析】【解答】解:A、折起后有重叠的面,不能围成正方体;
B、折起后没有重叠的面,能围成正方体;
C、折起后有重叠的面,不能围成正方体;
D、折起后没有重叠的面,能围成正方体.
故答案为:BD
【分析】把其中一个面作为底面,然后确定另外的面,如果另外的面不重叠就能折成正方体,如果重叠就不能折成正方体.
10.【答案】9;5;5
【解析】【解答】1个正方体的体积是1×1×1=1(立方厘米),1+3+5=9(个),一共9个正方体,体积是9立方厘米;
1个正方体的一个面的面积是1×1=1(平方厘米),底面一共5个面,它的占地面积是5平方厘米;
从右面能看到5个面,看到的面积是5平方厘米。
故答案为:9;5;5 。
【分析】棱长×棱长×棱长=体积;棱长×棱长=面积。
11.【答案】 5;8;11;14;17
【解析】【解答】解:填表如下:
故答案为:5;8;11;14;17。
【分析】下面没有露在外面,所以第一个长方体有5个面露在外面;每增加一个长方体露在外面的面就会增加3个,按照规律计算露在外面的面的个数即可。
12.【答案】 90
【解析】【解答】解:折成的正方体如图:
折成后的立方体的上面、前面和右面上的数字分别是5,3,6,它们的积最大,5×3×6=90
故答案为:90
【分析】把2作为底面,4、6就是左右面,5是上面,3是前面,1是后面,然后确定公顶点的三个数字最大是多少,再求出乘积即可.
四、解答题
13.【答案】 解:
最大面重合的包装方法最省纸.
【解析】【解答】根据排列层数及重合面的不同,有 :
包装法。? 最大面重合的包装方法最省纸.
【分析】本题考查逆向思维问题的能力。
14.【答案】 (1)
(2)(3×5+3×1+1×5)×2
=23×2
=46(平方厘米)
答: 这个火柴盒的表面积是46平方厘米。
【解析】【分析】(1)标数据时可以根据数量的大小和展开图综合判断;
(2)长方体表面积=(长×宽+长×高+宽×高)×2.
五、综合题
15.【答案】 (1)E
(2)E
(3)经过测量,这个长方体的长是30毫米,宽是20毫米,高是10毫米,
(30×20+20×10+30×10)×2=2200(平方毫米)
答:这个长方体的表面积是2200平方毫米。
【解析】【解答】解:(1)如果A面在底部,那么E面在上面;
(2)如果F面在前面,从左面看是B面,E面在上面;
【分析】(1)从图中可以看出,A的相对面是E,所以如果A面在底部,那么E面在上面;
(2)如果F面在前面,从左面看是B面,与B面和F面连接的两个面分别是E面和D面,根据F面和B面的位置可以得出E面在上面;
(3)量出长方体的长、宽、高的长度,长方体的表面积=(长×宽+长×高+宽 ×高)×2,然后代入数据作答即可。
六、应用题
16.【答案】 解:3×3×6﹣1×1×2+1×3×4
=54﹣2+12
=64(平方厘米)
答:挖洞后的木块的表面积是64平方厘米.
【解析】【分析】根据题干,挖洞后的木块的表面积在减少2个1×1面的同时,增加了4个1×3的面的面积,据此计算即可解答问题.
