五年级上册数学一课一练-4.15组合图形的面积 浙教版(含答案)
文档属性
| 名称 | 五年级上册数学一课一练-4.15组合图形的面积 浙教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 91.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-20 00:00:00 | ||
图片预览

文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级上册数学一课一练-4.15组合图形的面积
一、单选题
1.下面三幅图中,正方形一样大,则三个阴影部分的面积(??? )
A.?一样大??????????????????????B.?第一幅图最大??????????????????????C.?第二幅图最大??????????????????????D.?第三幅图最大
2.下图的长方形被分成甲、乙两部分,下列说法正确的是( ??)。
A.?甲、乙周长相等,面积不相等。
B.?甲、乙周长不相等,面积相等。
C.?甲、乙周长相等,面积也相等。
3.在图中的平行四边形中,甲的面积( )乙的面积.
A.?大于??????????????????????????????????B.?小于??????????????????????????????????C.?等于??????????????????????????????????D.?无法确定
4.等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则腰长(????? )。
A.?24厘米???????????????????????????????B.?12厘米???????????????????????????????C.?18厘米???????????????????????????????D.?36厘米
二、判断题
5.计算组合图形的面积也要用到基本图形的面积公式。
6.如图是我国珍贵的历史文化遗产《易经》中的一个主要图形﹣﹣﹣太极图,它是数形结合的光辉典范.图中阴阳(即圈内黑白)两部分的面积相等.(判断对错)
7.用8个大小一样的正方形无论拼成什么图形,它们的面积都相等。(??? )
三、填空题
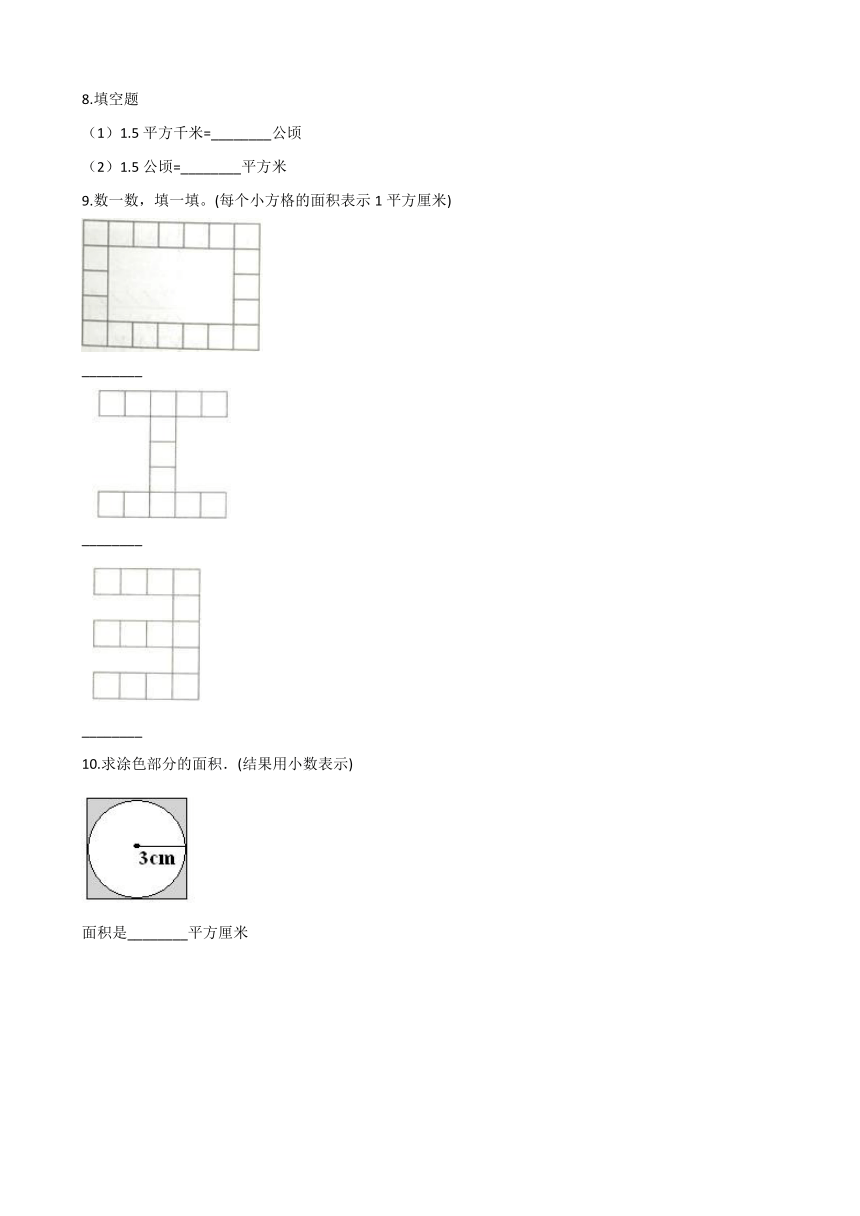
8.填空题
(1)1.5平方千米=________公顷
(2)1.5公顷=________平方米
9.数一数,填一填。(每个小方格的面积表示1平方厘米)
________
?
________
?
________
10.求涂色部分的面积.(结果用小数表示)
面积是________平方厘米
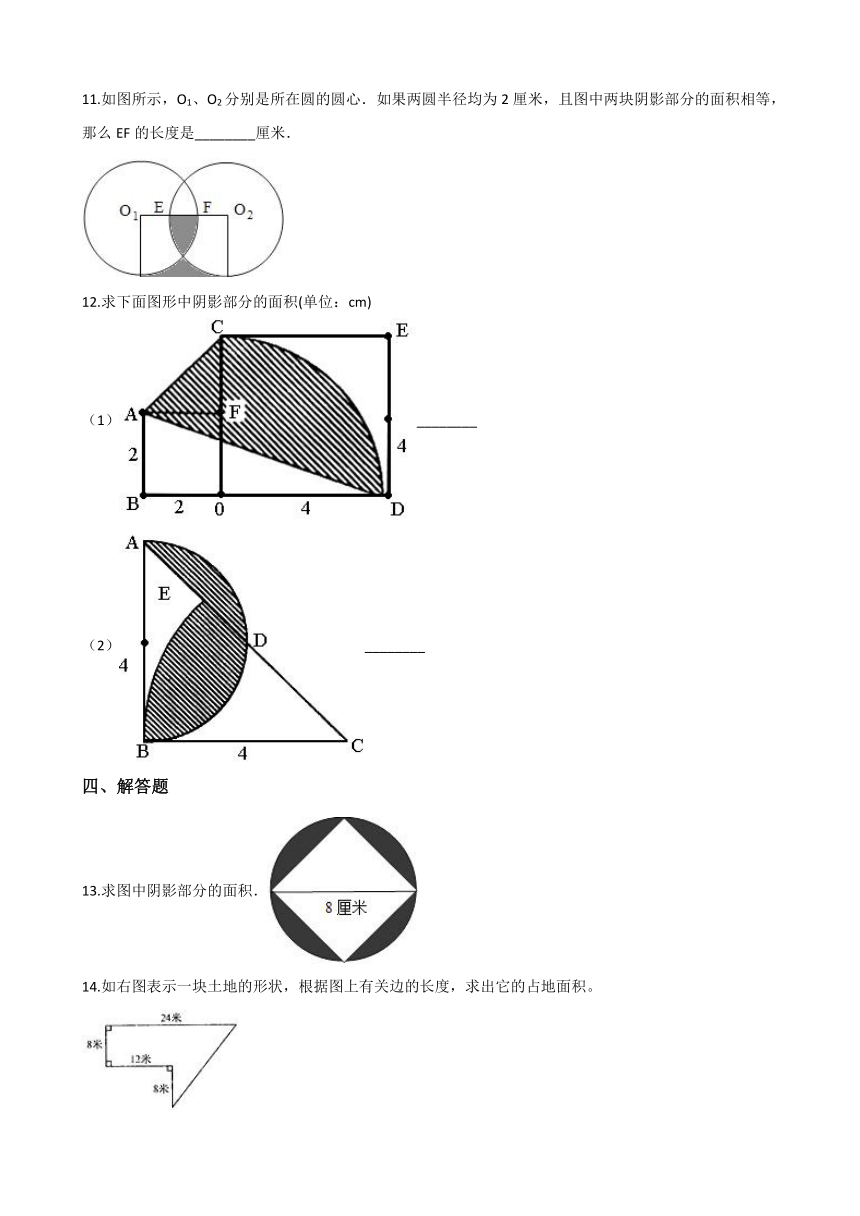
11.如图所示,O1、O2分别是所在圆的圆心.如果两圆半径均为2厘米,且图中两块阴影部分的面积相等,那么EF的长度是________厘米.
12.求下面图形中阴影部分的面积(单位:cm)
(1)________
(2)________
四、解答题
13.求图中阴影部分的面积.
14.如右图表示一块土地的形状,根据图上有关边的长度,求出它的占地面积。
五、综合题
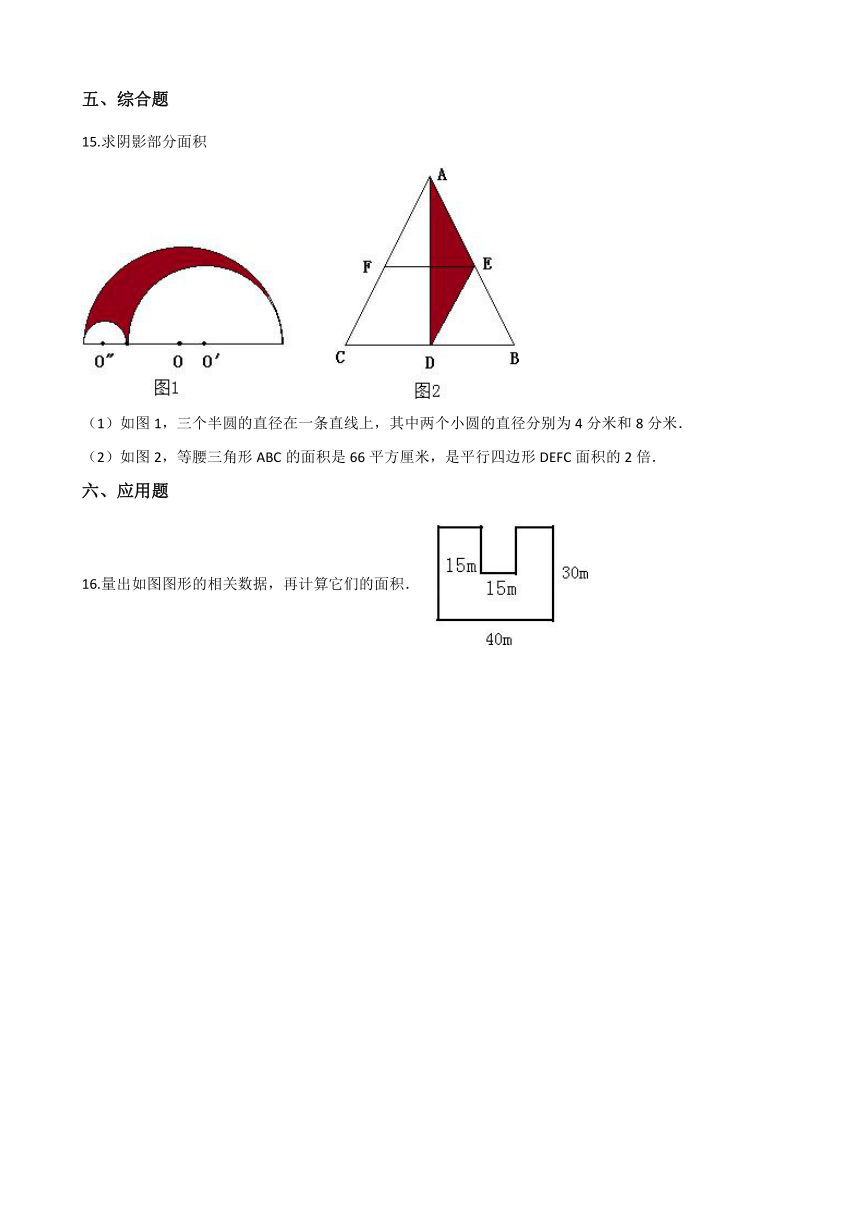
15.求阴影部分面积
(1)如图1,三个半圆的直径在一条直线上,其中两个小圆的直径分别为4分米和8分米.
(2)如图2,等腰三角形ABC的面积是66平方厘米,是平行四边形DEFC面积的2倍.
六、应用题
16.量出如图图形的相关数据,再计算它们的面积.
参考答案
一、单选题
1.【答案】 A
【解析】【解答】假设正方形的边长是4,
第一个图形:
4×4-3.14×(4÷2)?
=16-3.14×4
=16-12.56
=3.44
第二个图形:
4×4-3.14×(4÷4)?×4
=16-3.14×4
=16-12.56
=3.44
第三个图形:
4×4-3.14×4?÷4
=16-3.14×4
=16-12.56
=3.44
所以三个阴影部分的面积一样大.
故答案为:A
【分析】三个阴影部分的面积都是正方形面积减去内部空白部分的面积,假设出正方形的边长,然后根据正方形和圆面积公式分别计算阴影部分的面积并作出判断即可.
2.【答案】 A
【解析】【解答】 下图的长方形被分成甲、乙两部分,, 甲、乙周长相等,面积不相等.
故答案为:A.
【分析】观察图可知,甲的周长=长+宽+曲线部分的长度,乙的周长=长+宽+曲线部分的长度,甲的面积>乙的面积,据此解答.
3.【答案】C
【解析】【解答】解:因为三角形甲和上面的空白三角形与三角形乙和上面的空白三角形,组成了两个等底等高的大三角形,
都去掉公共部分,即上面的空白三角形,剩下的面积仍然相等,即甲的面积等于乙的面积;
故选:C.
【分析】由题意可知,三角形甲和上面的空白三角形与三角形乙和上面的空白三角形,组成了两个等底等高的大三角形,都去掉公共部分,即上面的空白三角形,剩下的面积仍然相等,即甲的面积等于乙的面积,据此解答即可.
4.【答案】 B
【解析】【解答】根据题干可得,梯形的上底与下底的和为:96×2÷8=24(厘米)
梯形的腰长为:
(48-24)÷2
=24÷2
=12〔厘米〕
故选:B
【分析】根据题干,可以利用梯形的面积公式先求出上底加下底的和是多少,再利用周长求得两腰的长度。
二、判断题
5.【答案】正确
【解析】【解答】计算组合图形的面积时,要用到长方形的面积、正方形的面积、三角形的面积等基本图形的面积公式。
故答案为:正确。
【分析】组合图形均是由一些基本图形组合起来的。在计算组合图形的面积时,可利用出入相补的方法对图形进行移动、重组,而图形的面积大小不变,利用一些基本公式进行计算,由此即可得出答案。
6.【答案】正确
【解析】【解答】解:把小黑圆补充到小白圆上,黑白两部分是相等的,原题说法正确.
故答案为:正确
【分析】把图形重新组合后判断出这两部分的面积都是这个圆面积的一半,由此判断即可.
7.【答案】 正确
【解析】【解答】解:用8个大小一样的正方形无论拼成什么图形,它们的面积都相等。
故答案为:正确。
【分析】用8个大小一样的正方形无论拼成什么图形,都是这8个正方形的面积,所以它们的面积都相等。
三、填空题
8.【答案】(1)150
(2)15000
【解析】
9.【答案】20平方厘米 ;13平方厘米 ;14平方厘米
【解析】【解答】20平方厘米? 13平方厘米? 14平方厘米
【分析】运用数方格的方法即可求解,考察了规则图形的面积。
10.【答案】7.74
【解析】【解答】解:3×2=6(厘米)
6×6-3.14×3?
=36-28.26
=7.74(平方厘米)
故答案为:7.74
【分析】用正方形面积减去空白部分圆面积就是涂色部分的面积,圆面积公式:S=πr?,正方形面积=边长×边长。
11.【答案】0.86
【解析】【解答】解:因为两个阴影部分的面积相等,所以长方形的面积等于扇形面积的2倍,
而其中一个扇形的面积= π×22=π(cm2),
故整个长方形的面积=2π(cm2),
故两个圆心连接的线段O1O2=面积÷宽=2π÷2=π(cm),
故EF=2+2﹣π=4﹣π=4﹣3.14=0.86(cm).
答:EF的长度是0.86厘米.
故答案为:0.86.
【分析】根据长方形中,一个空白部分的面积加上其中一个阴影部分的面积等于另一个空白部分面积加上另一个阴影部分的面积可得长方形的面积等于扇形面积的2倍,从而可求长方形的面积,再根据线段之间的和差关系求解即可.考查了组合图形的面积,本题难度较大,解题的关键是得到整个长方形的面积.
12.【答案】(1)?
(2)
【解析】【解答】解:(1)2×2+4×4+2×2÷2
=4+16+2
=22(cm?)
(2+4)×2÷2=6(cm?)
4×4-π×4?÷4
=16-4π(cm?)
阴影部分面积:22-6-(16-4π)=16-16+4π=4π(cm?);
(2)π×(4÷2)?÷2-[4×4÷2-π×4?×]
=π×2-(8-π×2)
=2π-8+2π
=4π-8(cm?)
故答案为:(16-4π)cm?;(4π-8)cm?
【分析】(1)阴影部分的面积是两个正方形面积加上左上角三角形的面积,减去图中两块空白部分的面积,左边空白部分是三角形,右边空白部分是正方形面积减去扇形面积;(2)阴影部分的面积是半圆面积减去半圆内空白部分的面积,空白部分的面积是三角形ABC的面积减去扇形面积,扇形面积是所在圆面积的.
四、解答题
13.【答案】解:3.14×(8÷2)2-8×(8÷2)÷2×2=18.24(平方厘米)
答:阴影部分的面积是18.24平方厘米.
【解析】【分析】阴影部分面积等于直径是8厘米圆的面积减去底边是8厘米、底边上高是(8÷2)厘米的三角形面积的2倍,据此计算即可.
14.【答案】解:8×12+ ×(24-12)×(8+8)
=96+96
=192(平方米)
答:它的占地面积是192平方米.
【解析】【分析】把图形分成左边一个长方形、右边一个三角形分别来计算面积,注意右边直角三角形的两条直角边分别是(24-12)米和(8+8)米.
五、综合题
15.【答案】 (1)解:
大半圆面积:3.14×[(4+8)÷2]2÷2,
=3.14×36÷2,
=113.04÷2,
=56.52(平方分米),半圆面积和:3.14×(4÷2)2÷2+3.14×(8÷2)2÷2,
=3.14×4÷2+3.14×16÷2,
=6.28+25.12,
=31.4(平方分米),
阴影面积:56.52﹣31.4=25.12(平方分米).
答:阴影部分为25.12平方分米
(2)解:三角形AED的面积是平行四边形DEFC的面积的 ,平行四边形DEFC的面积是三角形ABC面积的 ;
阴影部分的面积:66× × =16.5(平方厘米).
答:阴影部分的面积是16.5平方厘米
【解析】【分析】(1)大半圆的直径为两个小半圆直径之和,运用公式s半圆=π×(d÷2)2÷2可分别求出三个半圆面积,大半圆面积减去两个小半圆的面积即为阴影部分面积;(2)平行四边形DEFC与三角形ADE等底等高,所以三角形AED的面积是平行四边形DEFC的面积的 ,平行四边形DEFC的面积是三角形阿ABC面积的 ;由此解决问题.此题主要灵活运用圆的面积,平行四边形与三角形的面积计算之间的联系来解决问题.
六、应用题
16.【答案】解:40×30﹣15×15 =1200﹣225
=975(平方米)
答:这个图形的面积是975平方米
【解析】【分析】这个图形的面积就等于长方形的面积减去正方形的面积,利用长方形的面积公式S=ab和正方形的面积公式S=a×a即可求解.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级上册数学一课一练-4.15组合图形的面积
一、单选题
1.下面三幅图中,正方形一样大,则三个阴影部分的面积(??? )
A.?一样大??????????????????????B.?第一幅图最大??????????????????????C.?第二幅图最大??????????????????????D.?第三幅图最大
2.下图的长方形被分成甲、乙两部分,下列说法正确的是( ??)。
A.?甲、乙周长相等,面积不相等。
B.?甲、乙周长不相等,面积相等。
C.?甲、乙周长相等,面积也相等。
3.在图中的平行四边形中,甲的面积( )乙的面积.
A.?大于??????????????????????????????????B.?小于??????????????????????????????????C.?等于??????????????????????????????????D.?无法确定
4.等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则腰长(????? )。
A.?24厘米???????????????????????????????B.?12厘米???????????????????????????????C.?18厘米???????????????????????????????D.?36厘米
二、判断题
5.计算组合图形的面积也要用到基本图形的面积公式。
6.如图是我国珍贵的历史文化遗产《易经》中的一个主要图形﹣﹣﹣太极图,它是数形结合的光辉典范.图中阴阳(即圈内黑白)两部分的面积相等.(判断对错)
7.用8个大小一样的正方形无论拼成什么图形,它们的面积都相等。(??? )
三、填空题
8.填空题
(1)1.5平方千米=________公顷
(2)1.5公顷=________平方米
9.数一数,填一填。(每个小方格的面积表示1平方厘米)
________
?
________
?
________
10.求涂色部分的面积.(结果用小数表示)
面积是________平方厘米
11.如图所示,O1、O2分别是所在圆的圆心.如果两圆半径均为2厘米,且图中两块阴影部分的面积相等,那么EF的长度是________厘米.
12.求下面图形中阴影部分的面积(单位:cm)
(1)________
(2)________
四、解答题
13.求图中阴影部分的面积.
14.如右图表示一块土地的形状,根据图上有关边的长度,求出它的占地面积。
五、综合题
15.求阴影部分面积
(1)如图1,三个半圆的直径在一条直线上,其中两个小圆的直径分别为4分米和8分米.
(2)如图2,等腰三角形ABC的面积是66平方厘米,是平行四边形DEFC面积的2倍.
六、应用题
16.量出如图图形的相关数据,再计算它们的面积.
参考答案
一、单选题
1.【答案】 A
【解析】【解答】假设正方形的边长是4,
第一个图形:
4×4-3.14×(4÷2)?
=16-3.14×4
=16-12.56
=3.44
第二个图形:
4×4-3.14×(4÷4)?×4
=16-3.14×4
=16-12.56
=3.44
第三个图形:
4×4-3.14×4?÷4
=16-3.14×4
=16-12.56
=3.44
所以三个阴影部分的面积一样大.
故答案为:A
【分析】三个阴影部分的面积都是正方形面积减去内部空白部分的面积,假设出正方形的边长,然后根据正方形和圆面积公式分别计算阴影部分的面积并作出判断即可.
2.【答案】 A
【解析】【解答】 下图的长方形被分成甲、乙两部分,, 甲、乙周长相等,面积不相等.
故答案为:A.
【分析】观察图可知,甲的周长=长+宽+曲线部分的长度,乙的周长=长+宽+曲线部分的长度,甲的面积>乙的面积,据此解答.
3.【答案】C
【解析】【解答】解:因为三角形甲和上面的空白三角形与三角形乙和上面的空白三角形,组成了两个等底等高的大三角形,
都去掉公共部分,即上面的空白三角形,剩下的面积仍然相等,即甲的面积等于乙的面积;
故选:C.
【分析】由题意可知,三角形甲和上面的空白三角形与三角形乙和上面的空白三角形,组成了两个等底等高的大三角形,都去掉公共部分,即上面的空白三角形,剩下的面积仍然相等,即甲的面积等于乙的面积,据此解答即可.
4.【答案】 B
【解析】【解答】根据题干可得,梯形的上底与下底的和为:96×2÷8=24(厘米)
梯形的腰长为:
(48-24)÷2
=24÷2
=12〔厘米〕
故选:B
【分析】根据题干,可以利用梯形的面积公式先求出上底加下底的和是多少,再利用周长求得两腰的长度。
二、判断题
5.【答案】正确
【解析】【解答】计算组合图形的面积时,要用到长方形的面积、正方形的面积、三角形的面积等基本图形的面积公式。
故答案为:正确。
【分析】组合图形均是由一些基本图形组合起来的。在计算组合图形的面积时,可利用出入相补的方法对图形进行移动、重组,而图形的面积大小不变,利用一些基本公式进行计算,由此即可得出答案。
6.【答案】正确
【解析】【解答】解:把小黑圆补充到小白圆上,黑白两部分是相等的,原题说法正确.
故答案为:正确
【分析】把图形重新组合后判断出这两部分的面积都是这个圆面积的一半,由此判断即可.
7.【答案】 正确
【解析】【解答】解:用8个大小一样的正方形无论拼成什么图形,它们的面积都相等。
故答案为:正确。
【分析】用8个大小一样的正方形无论拼成什么图形,都是这8个正方形的面积,所以它们的面积都相等。
三、填空题
8.【答案】(1)150
(2)15000
【解析】
9.【答案】20平方厘米 ;13平方厘米 ;14平方厘米
【解析】【解答】20平方厘米? 13平方厘米? 14平方厘米
【分析】运用数方格的方法即可求解,考察了规则图形的面积。
10.【答案】7.74
【解析】【解答】解:3×2=6(厘米)
6×6-3.14×3?
=36-28.26
=7.74(平方厘米)
故答案为:7.74
【分析】用正方形面积减去空白部分圆面积就是涂色部分的面积,圆面积公式:S=πr?,正方形面积=边长×边长。
11.【答案】0.86
【解析】【解答】解:因为两个阴影部分的面积相等,所以长方形的面积等于扇形面积的2倍,
而其中一个扇形的面积= π×22=π(cm2),
故整个长方形的面积=2π(cm2),
故两个圆心连接的线段O1O2=面积÷宽=2π÷2=π(cm),
故EF=2+2﹣π=4﹣π=4﹣3.14=0.86(cm).
答:EF的长度是0.86厘米.
故答案为:0.86.
【分析】根据长方形中,一个空白部分的面积加上其中一个阴影部分的面积等于另一个空白部分面积加上另一个阴影部分的面积可得长方形的面积等于扇形面积的2倍,从而可求长方形的面积,再根据线段之间的和差关系求解即可.考查了组合图形的面积,本题难度较大,解题的关键是得到整个长方形的面积.
12.【答案】(1)?
(2)
【解析】【解答】解:(1)2×2+4×4+2×2÷2
=4+16+2
=22(cm?)
(2+4)×2÷2=6(cm?)
4×4-π×4?÷4
=16-4π(cm?)
阴影部分面积:22-6-(16-4π)=16-16+4π=4π(cm?);
(2)π×(4÷2)?÷2-[4×4÷2-π×4?×]
=π×2-(8-π×2)
=2π-8+2π
=4π-8(cm?)
故答案为:(16-4π)cm?;(4π-8)cm?
【分析】(1)阴影部分的面积是两个正方形面积加上左上角三角形的面积,减去图中两块空白部分的面积,左边空白部分是三角形,右边空白部分是正方形面积减去扇形面积;(2)阴影部分的面积是半圆面积减去半圆内空白部分的面积,空白部分的面积是三角形ABC的面积减去扇形面积,扇形面积是所在圆面积的.
四、解答题
13.【答案】解:3.14×(8÷2)2-8×(8÷2)÷2×2=18.24(平方厘米)
答:阴影部分的面积是18.24平方厘米.
【解析】【分析】阴影部分面积等于直径是8厘米圆的面积减去底边是8厘米、底边上高是(8÷2)厘米的三角形面积的2倍,据此计算即可.
14.【答案】解:8×12+ ×(24-12)×(8+8)
=96+96
=192(平方米)
答:它的占地面积是192平方米.
【解析】【分析】把图形分成左边一个长方形、右边一个三角形分别来计算面积,注意右边直角三角形的两条直角边分别是(24-12)米和(8+8)米.
五、综合题
15.【答案】 (1)解:
大半圆面积:3.14×[(4+8)÷2]2÷2,
=3.14×36÷2,
=113.04÷2,
=56.52(平方分米),半圆面积和:3.14×(4÷2)2÷2+3.14×(8÷2)2÷2,
=3.14×4÷2+3.14×16÷2,
=6.28+25.12,
=31.4(平方分米),
阴影面积:56.52﹣31.4=25.12(平方分米).
答:阴影部分为25.12平方分米
(2)解:三角形AED的面积是平行四边形DEFC的面积的 ,平行四边形DEFC的面积是三角形ABC面积的 ;
阴影部分的面积:66× × =16.5(平方厘米).
答:阴影部分的面积是16.5平方厘米
【解析】【分析】(1)大半圆的直径为两个小半圆直径之和,运用公式s半圆=π×(d÷2)2÷2可分别求出三个半圆面积,大半圆面积减去两个小半圆的面积即为阴影部分面积;(2)平行四边形DEFC与三角形ADE等底等高,所以三角形AED的面积是平行四边形DEFC的面积的 ,平行四边形DEFC的面积是三角形阿ABC面积的 ;由此解决问题.此题主要灵活运用圆的面积,平行四边形与三角形的面积计算之间的联系来解决问题.
六、应用题
16.【答案】解:40×30﹣15×15 =1200﹣225
=975(平方米)
答:这个图形的面积是975平方米
【解析】【分析】这个图形的面积就等于长方形的面积减去正方形的面积,利用长方形的面积公式S=ab和正方形的面积公式S=a×a即可求解.
同课章节目录
