苏科版数学七年级下册:7.5 多边形的内角和与外角和 同步训练(解析版)
文档属性
| 名称 | 苏科版数学七年级下册:7.5 多边形的内角和与外角和 同步训练(解析版) |
|
|
| 格式 | zip | ||
| 文件大小 | 147.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-19 00:00:00 | ||
图片预览

文档简介
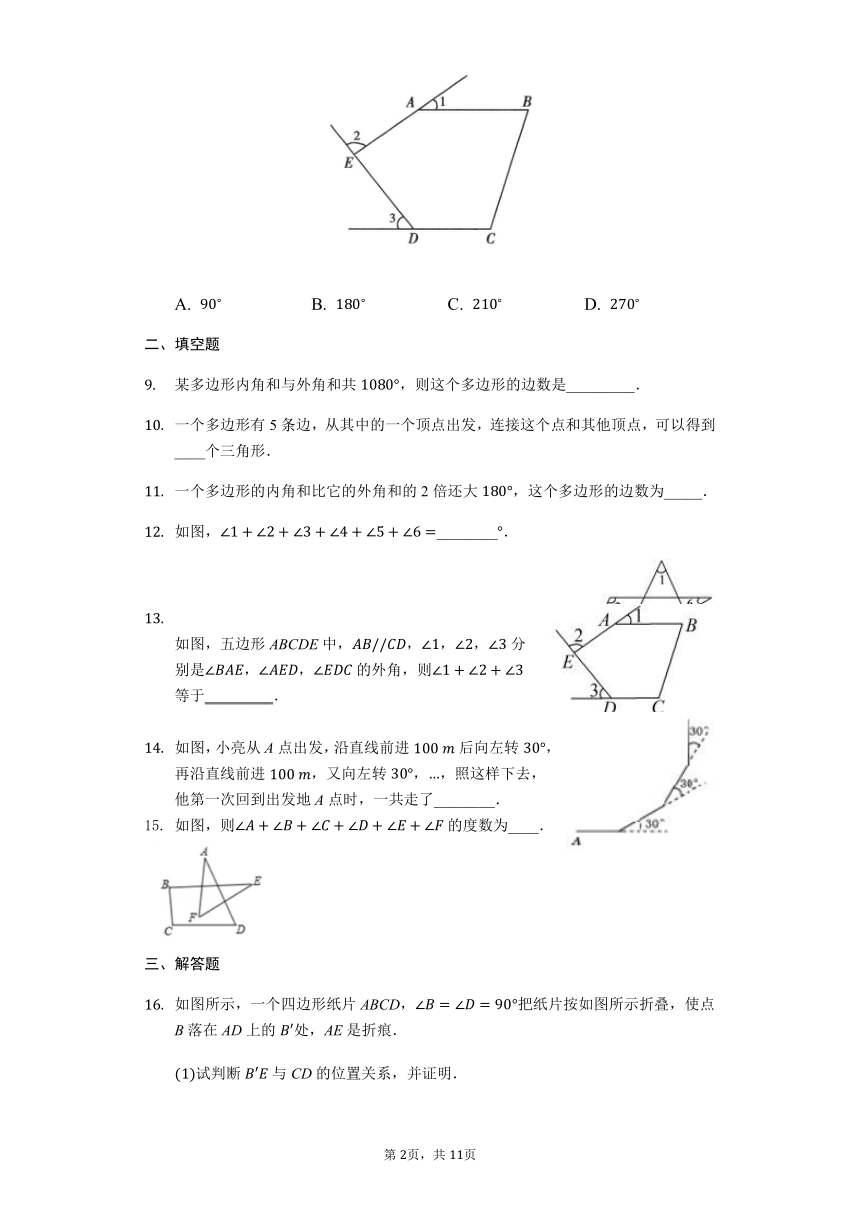
七下第七章7.5多边形的内角和与外角和基础题训练
一、选择题
一个多边形的内角和是外角和的2倍,这个多边形是
A. 四边形 B. 五边形 C. 六边形 D. 八边形
从多边形一个顶点出发向其余的顶点引对角线,将多边形分成6个三角形,则此多边形的边数为???
A. 6 B. 7 C. 8 D. 9
一个n边形的内角和比它的外角和大,则n等于
A. 3 B. 4 C. 5 D. 6
下列图形具有稳定性的是
A. 三角形 B. 四边形 C. 五边形 D. 六边形
若一个多边形的每一个内角都等于,则它是? ? ?
A. 四边形 B. 五边形 C. 六边形 D. 八边形
如图,一艘轮船行驶在点O处同时测得海岛A、B的方向分别是北偏东和西北方向,则的度数是
A.
B.
C.
D.
将一副直角三角板如图放置,使含角的三角板的一条直角边和含角的三角板的一条直角边重合,则的度数为
A. B. C. D.
如图所示,在五边形ABCDE中,,、分别是、、的外角,则等于
A. B. C. D.
二、填空题
某多边形内角和与外角和共,则这个多边形的边数是_________.
一个多边形有5条边,从其中的一个顶点出发,连接这个点和其他顶点,可以得到____个三角形.
一个多边形的内角和比它的外角和的2倍还大,这个多边形的边数为_____.
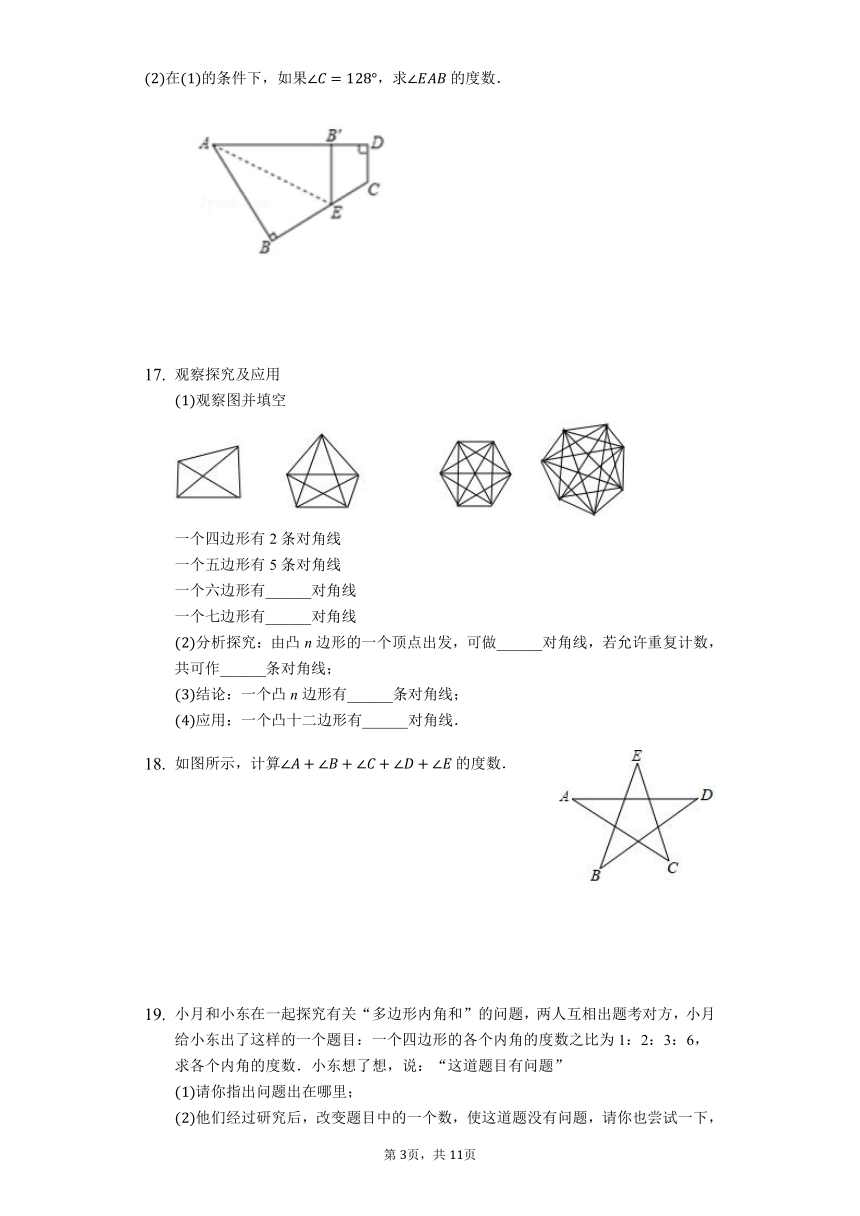
如图,________.
如图,五边形ABCDE中,,,,分别是,,的外角,则等于_________.
如图,小亮从A点出发,沿直线前进后向左转,再沿直线前进,又向左转,,照这样下去,他第一次回到出发地A点时,一共走了________.
如图,则的度数为____.
三、解答题
如图所示,一个四边形纸片ABCD,把纸片按如图所示折叠,使点B落在AD上的处,AE是折痕.
试判断与CD的位置关系,并证明.
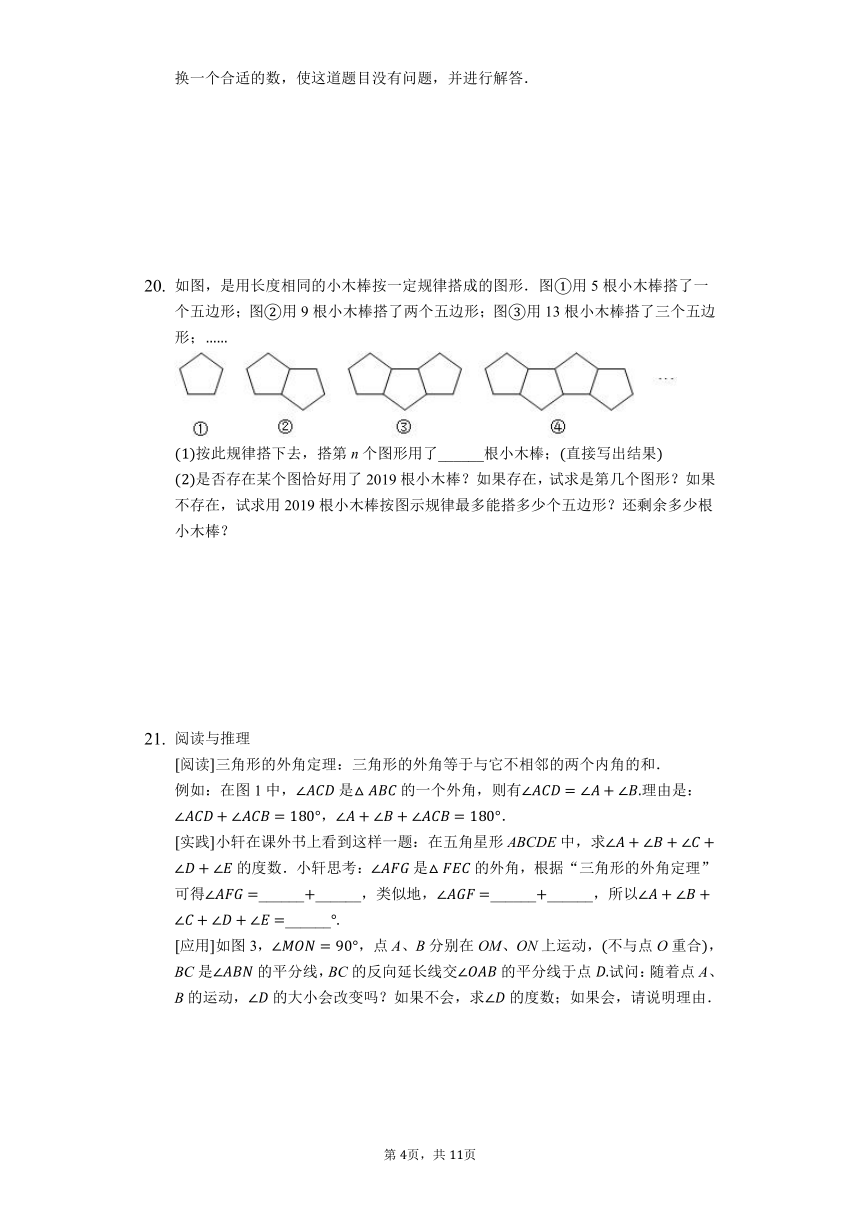
在的条件下,如果,求的度数.
观察探究及应用
观察图并填空
一个四边形有2条对角线
一个五边形有5条对角线
一个六边形有______对角线
一个七边形有______对角线
分析探究:由凸n边形的一个顶点出发,可做______对角线,若允许重复计数,共可作______条对角线;
结论:一个凸n边形有______条对角线;
应用:一个凸十二边形有______对角线.
如图所示,计算的度数.
小月和小东在一起探究有关“多边形内角和”的问题,两人互相出题考对方,小月给小东出了这样的一个题目:一个四边形的各个内角的度数之比为1:2:3:6,求各个内角的度数.小东想了想,说:“这道题目有问题”
请你指出问题出在哪里;
他们经过研究后,改变题目中的一个数,使这道题没有问题,请你也尝试一下,换一个合适的数,使这道题目没有问题,并进行解答.
如图,是用长度相同的小木棒按一定规律搭成的图形.图用5根小木棒搭了一个五边形;图用9根小木棒搭了两个五边形;图用13根小木棒搭了三个五边形;
按此规律搭下去,搭第n个图形用了______根小木棒;直接写出结果
是否存在某个图恰好用了2019根小木棒?如果存在,试求是第几个图形?如果不存在,试求用2019根小木棒按图示规律最多能搭多少个五边形?还剩余多少根小木棒?
阅读与推理
阅读三角形的外角定理:三角形的外角等于与它不相邻的两个内角的和.
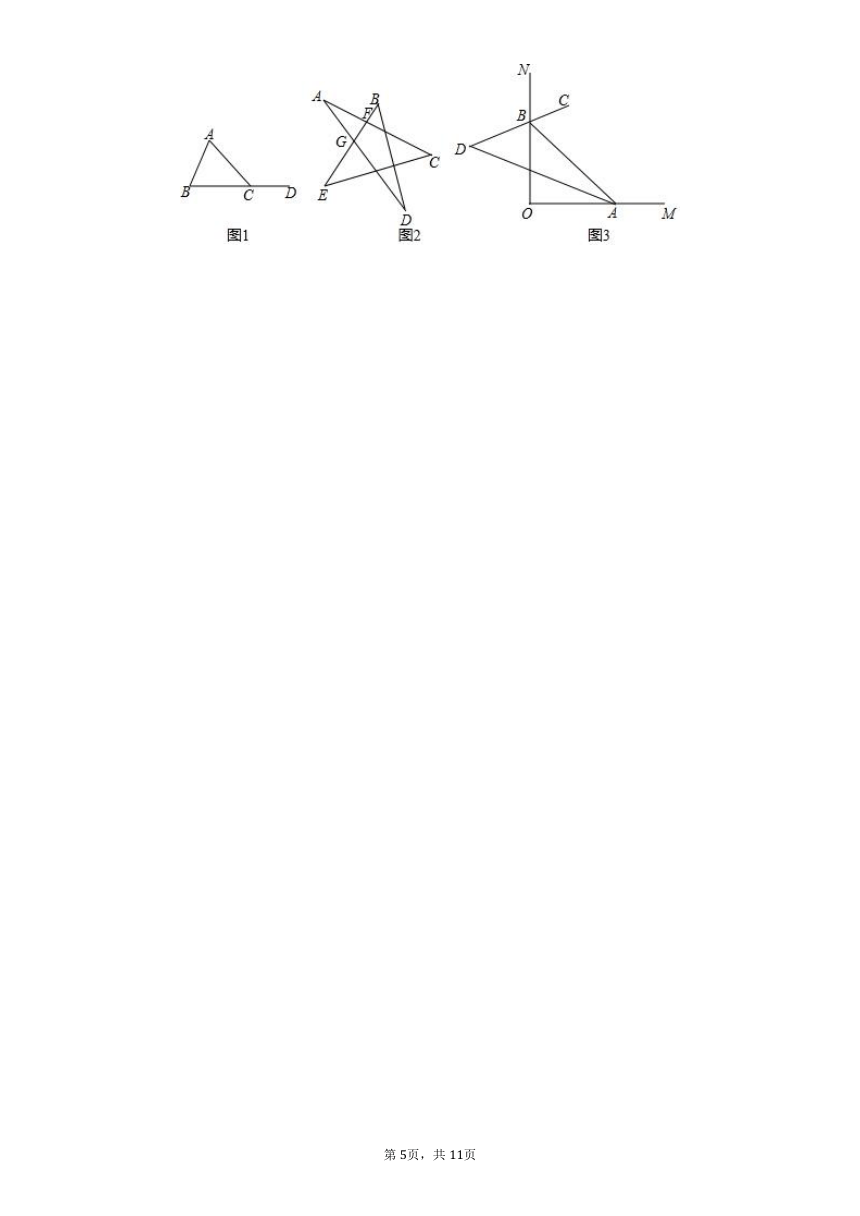
例如:在图1中,是的一个外角,则有理由是:,.
实践小轩在课外书上看到这样一题:在五角星形ABCDE中,求的度数.小轩思考:是的外角,根据“三角形的外角定理”可得____________,类似地,____________,所以______
应用如图3,,点A、B分别在OM、ON上运动,不与点O重合,BC是的平分线,BC的反向延长线交的平分线于点试问:随着点A、B的运动,的大小会改变吗?如果不会,求的度数;如果会,请说明理由.
答案和解析
1.C
解:设所求多边形边数为n,
由题意得
解得.
则这个多边形是六边形.
2.C
解:这个多边形的边数是.
3.C
解:根据题意得:
,
解得.
4.A
解:具有稳定性的图形是三角形.
5.B
解:一个多边形的每一个内角都等于,
一个多边形的每一个外角都等于,
多边形的边数.
6.C
7.D
解:由三角形的外角性质得,
,
.
8.B
,,B、两角的外角和是.
五边形外角和是,
9.6
解:多边形内角和与外角和共,
多边形内角和,
设多边形的边数是n,
,解得.
10.3
解:n边形从一个顶点出发的对角线可以有条,这些对角线把多边形分成了个三角形,所以5边形从一个顶点出发的对角线,把多边形分成了3个三角形.
11.7
解:设这个多边形的边数是n,
根据题意得,,
.
12.
解:如图所示,,,
又,
.
13.
解:如图,
,
,
,
根据多边形的外角和定理,,
.
14.1200m
解:,
他需要走12次才会回到原来的起点,即一共走了.
15..
解:如图,
,,
.
16.解:,
证明:由折叠得:,
;
由得,,
由折叠得:.
又,
.
17. ? 14? ;?
? ;
??; ?
? .
解:根据图形数出对角线条数,一个四边形有2条对角线,一个五边形有5条对角线,一个六边形有9对角线,一个七边形有14对角线;
故答案为:9;14.
边形从一个顶点出发可引出条对角线,若允许重复计数,共可作条对角线;
故答案为:;.
由可知,任意凸n边形的对角线有条,故答案为:.
把代入计算得:.
18.解:如图,
是的外角,
,
同理可得,
在中,
,
.
19.解:设此四边形的四个内角度数为、、、,
则,
解得:,
所以最大的内角度数为,
则此多边形不是四边形;
将四边形的各个内角的度数之比为1:2:3:6改为1:2:3:4,
设此四边形的四个内角度数为、、、,
则,
解得:,
所以四边形的四个内角度数分别为、、,.
20.
解:图用根小木棒搭了一个五边形;图用了根小木棒搭了两个五边形;图用了根小木棒搭了三个五边形;
按此规律搭下去,搭第n个图形用了根小木棒,
故答案为:;
不存在,
,
,
故用2019根小木棒按图示规律最多能搭504个五边形,还剩余2根小木棒.
21. ? ? ? ? 180
解:在中,直接可得,在中,可得,
,,
;
故答案为,,;
设AD与BO相交于点E,
;
的度数不发生改变.
是的一个外角,是的一个外角,即可求解.
,用角平分线和三角形内角和进行等量代换即可;
第2页,共2页
第1页,共1页
一、选择题
一个多边形的内角和是外角和的2倍,这个多边形是
A. 四边形 B. 五边形 C. 六边形 D. 八边形
从多边形一个顶点出发向其余的顶点引对角线,将多边形分成6个三角形,则此多边形的边数为???
A. 6 B. 7 C. 8 D. 9
一个n边形的内角和比它的外角和大,则n等于
A. 3 B. 4 C. 5 D. 6
下列图形具有稳定性的是
A. 三角形 B. 四边形 C. 五边形 D. 六边形
若一个多边形的每一个内角都等于,则它是? ? ?
A. 四边形 B. 五边形 C. 六边形 D. 八边形
如图,一艘轮船行驶在点O处同时测得海岛A、B的方向分别是北偏东和西北方向,则的度数是
A.
B.
C.
D.
将一副直角三角板如图放置,使含角的三角板的一条直角边和含角的三角板的一条直角边重合,则的度数为
A. B. C. D.
如图所示,在五边形ABCDE中,,、分别是、、的外角,则等于
A. B. C. D.
二、填空题
某多边形内角和与外角和共,则这个多边形的边数是_________.
一个多边形有5条边,从其中的一个顶点出发,连接这个点和其他顶点,可以得到____个三角形.
一个多边形的内角和比它的外角和的2倍还大,这个多边形的边数为_____.
如图,________.
如图,五边形ABCDE中,,,,分别是,,的外角,则等于_________.
如图,小亮从A点出发,沿直线前进后向左转,再沿直线前进,又向左转,,照这样下去,他第一次回到出发地A点时,一共走了________.
如图,则的度数为____.
三、解答题
如图所示,一个四边形纸片ABCD,把纸片按如图所示折叠,使点B落在AD上的处,AE是折痕.
试判断与CD的位置关系,并证明.
在的条件下,如果,求的度数.
观察探究及应用
观察图并填空
一个四边形有2条对角线
一个五边形有5条对角线
一个六边形有______对角线
一个七边形有______对角线
分析探究:由凸n边形的一个顶点出发,可做______对角线,若允许重复计数,共可作______条对角线;
结论:一个凸n边形有______条对角线;
应用:一个凸十二边形有______对角线.
如图所示,计算的度数.
小月和小东在一起探究有关“多边形内角和”的问题,两人互相出题考对方,小月给小东出了这样的一个题目:一个四边形的各个内角的度数之比为1:2:3:6,求各个内角的度数.小东想了想,说:“这道题目有问题”
请你指出问题出在哪里;
他们经过研究后,改变题目中的一个数,使这道题没有问题,请你也尝试一下,换一个合适的数,使这道题目没有问题,并进行解答.
如图,是用长度相同的小木棒按一定规律搭成的图形.图用5根小木棒搭了一个五边形;图用9根小木棒搭了两个五边形;图用13根小木棒搭了三个五边形;
按此规律搭下去,搭第n个图形用了______根小木棒;直接写出结果
是否存在某个图恰好用了2019根小木棒?如果存在,试求是第几个图形?如果不存在,试求用2019根小木棒按图示规律最多能搭多少个五边形?还剩余多少根小木棒?
阅读与推理
阅读三角形的外角定理:三角形的外角等于与它不相邻的两个内角的和.
例如:在图1中,是的一个外角,则有理由是:,.
实践小轩在课外书上看到这样一题:在五角星形ABCDE中,求的度数.小轩思考:是的外角,根据“三角形的外角定理”可得____________,类似地,____________,所以______
应用如图3,,点A、B分别在OM、ON上运动,不与点O重合,BC是的平分线,BC的反向延长线交的平分线于点试问:随着点A、B的运动,的大小会改变吗?如果不会,求的度数;如果会,请说明理由.
答案和解析
1.C
解:设所求多边形边数为n,
由题意得
解得.
则这个多边形是六边形.
2.C
解:这个多边形的边数是.
3.C
解:根据题意得:
,
解得.
4.A
解:具有稳定性的图形是三角形.
5.B
解:一个多边形的每一个内角都等于,
一个多边形的每一个外角都等于,
多边形的边数.
6.C
7.D
解:由三角形的外角性质得,
,
.
8.B
,,B、两角的外角和是.
五边形外角和是,
9.6
解:多边形内角和与外角和共,
多边形内角和,
设多边形的边数是n,
,解得.
10.3
解:n边形从一个顶点出发的对角线可以有条,这些对角线把多边形分成了个三角形,所以5边形从一个顶点出发的对角线,把多边形分成了3个三角形.
11.7
解:设这个多边形的边数是n,
根据题意得,,
.
12.
解:如图所示,,,
又,
.
13.
解:如图,
,
,
,
根据多边形的外角和定理,,
.
14.1200m
解:,
他需要走12次才会回到原来的起点,即一共走了.
15..
解:如图,
,,
.
16.解:,
证明:由折叠得:,
;
由得,,
由折叠得:.
又,
.
17. ? 14? ;?
? ;
??; ?
? .
解:根据图形数出对角线条数,一个四边形有2条对角线,一个五边形有5条对角线,一个六边形有9对角线,一个七边形有14对角线;
故答案为:9;14.
边形从一个顶点出发可引出条对角线,若允许重复计数,共可作条对角线;
故答案为:;.
由可知,任意凸n边形的对角线有条,故答案为:.
把代入计算得:.
18.解:如图,
是的外角,
,
同理可得,
在中,
,
.
19.解:设此四边形的四个内角度数为、、、,
则,
解得:,
所以最大的内角度数为,
则此多边形不是四边形;
将四边形的各个内角的度数之比为1:2:3:6改为1:2:3:4,
设此四边形的四个内角度数为、、、,
则,
解得:,
所以四边形的四个内角度数分别为、、,.
20.
解:图用根小木棒搭了一个五边形;图用了根小木棒搭了两个五边形;图用了根小木棒搭了三个五边形;
按此规律搭下去,搭第n个图形用了根小木棒,
故答案为:;
不存在,
,
,
故用2019根小木棒按图示规律最多能搭504个五边形,还剩余2根小木棒.
21. ? ? ? ? 180
解:在中,直接可得,在中,可得,
,,
;
故答案为,,;
设AD与BO相交于点E,
;
的度数不发生改变.
是的一个外角,是的一个外角,即可求解.
,用角平分线和三角形内角和进行等量代换即可;
第2页,共2页
第1页,共1页
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
