华师大版八年级下册17.4反比例函数 教材同步拓展分层练习(含答案)
文档属性
| 名称 | 华师大版八年级下册17.4反比例函数 教材同步拓展分层练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 378.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-20 00:00:00 | ||
图片预览




文档简介
17.4 反比例函数
A卷:基础题
一、选择题
1.下列表达式中,表示y是x的反比例函数的是( )
①xy=-;②y=3-6x;③y=;④y=(m是常数,m≠0).
A.①②④ B.①③④ C.②③ D.①③
2.如图所示,A,C是函数y=的图象上任意两点,过点A作y轴的垂线,垂足为B,过点C作y轴的垂线,垂足为D,记Rt△AOB的面积为S1,Rt△COD的面积为S2,则( )
A.S1>S2 B.S1
3.在函数y=(k>0)的图象上有三点A1(x1,y1),A2(x2,y2),A3(x3,y3),已知x1
A B C D
二、填空题
5.已知y是x的反比例函数,当x=5时,y=-1,那么当y=3时,x=____,当x=3时,y=_____.
6.在下列反比例函数中,图象位于第一,三象限的有______;在其图象所在的每个象限内,y随x值的减小而减小的有_____.(填序号).
(1)y=-; (2)y=; (3)y=; (4)y=-.
7.已知点P(1,a)在反比例函数y=(k≠0)的图象上,其中a=m2+2m+3(m为实数),则这个函数的图象在第______象限内.
三、解答题
8.已知:y=y1-y2,y1与x成正比例,y2与x成反比例;当x=1时,y=0;当x=2时,y=3,求:(1)y与x之间的函数关系式;
(2)当x=6时,y的值.
四、思考题
9.如图18-4-3是某蓄水池每小时的排水量V(立方米/小时)与排完蓄水池中的水所用的时间t(小时)之间的函数图象.
(1)请你根据图象提供的信息求出此蓄水池的蓄水量;
(2)若要6小时排完蓄水池中的水,则每小时的排水量应该是多少?
B卷:提高题
一、七彩题
1.(多题一思路题)(1)当m取何值时,函数y=(m-1)|m|-2x为反比例函数?
(2)已知函数y=(m2-m-2)x,y可能是x的反比例函数吗?y可能是x的正比例函数吗?
2.(一题多变题)如图所示,一次函数y=kx-1与反比例函数y=的图象的一支在第一象限相交于点A,过点A作AB⊥x轴于点B,已知S△AOB=1,请求出反比例函数及一次函数的关系式.
(1)一变:如图所示,正比例函数y=k1x与反比例函数y=的图象的一支相交于第一象限的A点,已知A点坐标为(a,2a),过A点作AB⊥x轴于B,且S△AOB =4.①求A点的坐标;②求正比例函数和反比例函数的关系式;
(2)二变:如图所示,A,B两点是双曲线y=上关于原点对称的任意两点,分别过A,B两点作y轴,x轴的平行线,两线相交于点C,若S△ABC =4,求反比例函数的关系式.
二、知识交叉题
3.(科内交叉题)如图所示,直线y=-2x-2与双曲线y=的一支在第二象限交于点A,与x轴,y轴分别交于点B,C,AD⊥y轴于点D,若S△ADB =S△COB,求k的值.
三、实际应用题
4.某种商品有好的获利空间,但有不及时卖完的部分就要报废的风险.某商场希望通过这种商品获取50%的利润,商品的销售率为y(销售率=),价格倍数为x(价格倍数=).判断商品的销售率y与价格倍数x之间满足何种函数关系?
四、经典中考题
5.如图所示,一张正方形的纸片,剪去两个一样的小矩形得到一个“E”字形图案,设小矩形的长,宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数关系的图象是下图中的( )
A B C D
6.某反比例函数的图象经过点(-1,6),则下列各点中,此函数图象也经过的点是( )
A. (-3,2) B. (3,2) C. (2,3) D. (6,1)
7.(浙江杭州)如图,函数和函数的图象相交于点M(2,m),N(-1,n),若,则x的取值范围是( )
A. B.
C. D.
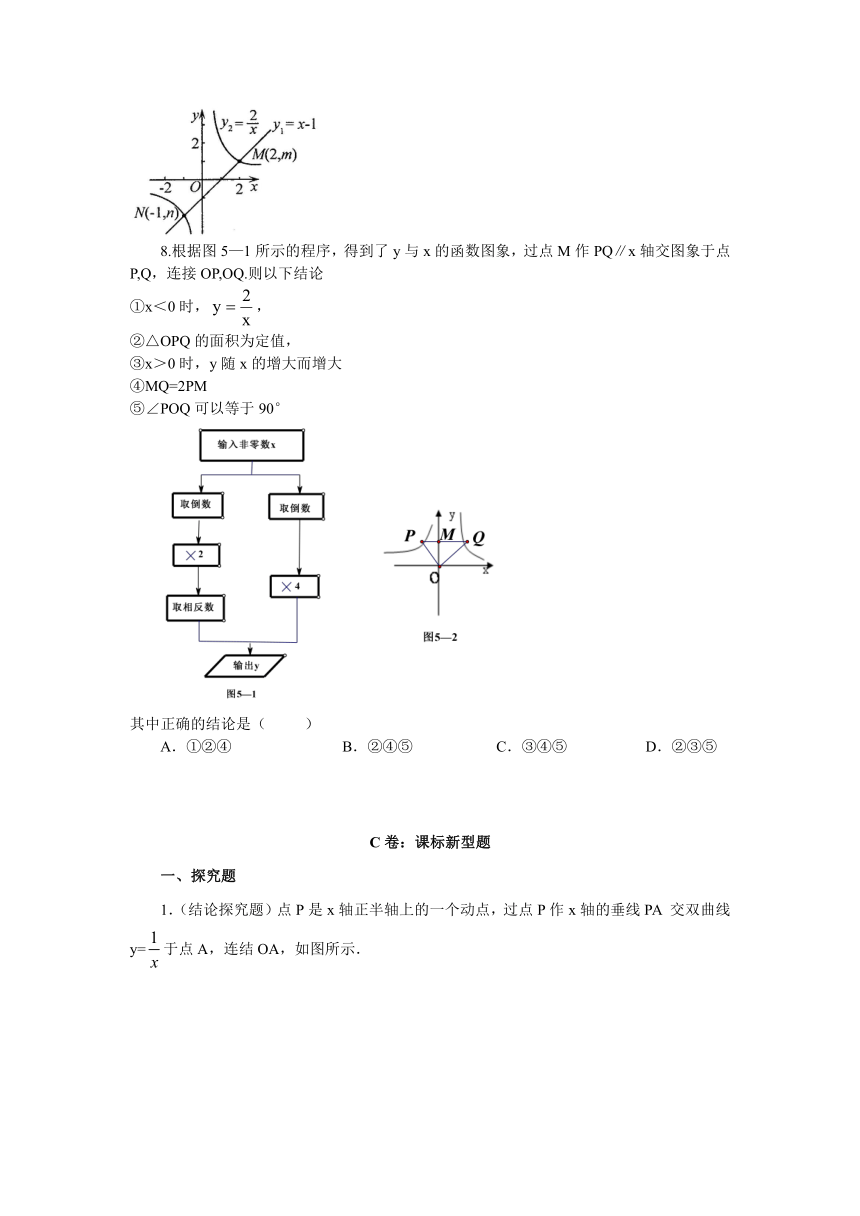
8.根据图5—1所示的程序,得到了y与x的函数图象,过点M作PQ∥x轴交图象于点P,Q,连接OP,OQ.则以下结论
①x<0时,,
②△OPQ的面积为定值,
③x>0时,y随x的增大而增大
④MQ=2PM
⑤∠POQ可以等于90°
其中正确的结论是( )
A.①②④ B.②④⑤ C.③④⑤ D.②③⑤
C卷:课标新型题
一、探究题
1.(结论探究题)点P是x轴正半轴上的一个动点,过点P作x轴的垂线PA交双曲线y=于点A,连结OA,如图所示.
(1)如图①,当点P在x轴的正方向上运动时,Rt△AOP的面积大小是否变化?若不变,请求出Rt△AOP的面积;若改变,试说明理由.
(2)如图②,在x轴上点P的右侧有一点D,过点D作x轴的垂线交双曲线于点B,连结OB交AP于点C.设△AOP的面积为S1,梯形BCPD的面积为S2,则S1与S2大小关系是S1______S2.
二、图表信息题
2.(图象信息题)已知三角形的面积为S,一条边长为a,这条边上的高为h.
(1)如果面积不变,那么h与a之间的函数关系是h=______,它们是_____函数关系.
(2)如图所示中的曲线是h关于a的函数图象,通过图象你能确定这个三角形的面积吗?
(3)观察图象,h随a的变化有怎样的变化?
三、归纳猜想题
3.已知y与x的部分取值如下表:
x -6 -5 -4 -3 -2 -1 2 3 4 5 6
y 1 1.2 1.5 2 3 6 -3 -2 -1.5 -1.2 -1
(1)试猜想y与x的函数关系可能是我们学过的哪类函数,并写出这个函数的关系式(不写x的取值范围);
(2)简要叙述该函数的性质.
4.现有一水池,容积为50m3,如果每小时注水xm3,则经过yh可以注满.试写出y与x的函数关系式,并画出其图象.在解答此题时,合作学习小组的李明同学的解答过程是:函数关系式为y=.用描点法画出函数y=的图象,如左图所示.
张旭同学的解答过程是:函数关系式为y=(x>0),用描点法画出函数y=(x>0)的图象,如右图所示,哪位同学的解答有错误?请讨论后指出存在的问题,并分析错误的原因.
参考答案
A卷
一、1.D 点拨:关键看函数关系式是否满足y=(k为常数,k≠0)的形式.
2.C 点拨:设A,C的坐标分别为(xA,yA),(xC,yC),则xA·yA=xC·yC=1,而S△AOB=│xA│·│yA│=xA·xA=,S△COD=│xC│·│yC│=(-xC)·(-yC)=xC·yC=×1=,所以S△AOB = S△COD.
3.C 点拨:当k>0时,反比例函数在每一个象限内,y随x的增大而减小.由于A1(x1,y1),A2(x2,y2)都在第三象限,x1
二、5.-;- 点拨:设y=(k≠0),因为x=5时,y=-1,则-1=,所以k=-5,所以y=-.所以当y=3时,3=-,x=-;当x=3时,y=-.
6.(2)(3);(1)(4) 点拨:当k>0时,反比例函数的图象位于第一,三象限,(2)中k=0.2>0,(3)中k=>0;当k<0时,反比例函数y随x的减小而减小,(1)中k=-<0,(4)中k=-50<0.
7.一,三 点拨:确定函数y=的图象所在的象限,就是确定k的符号.由于点(1,a)在函数y=的图象上,所以k=a,而a=m2+2m+3=(m+1)2+2>0,所以k>0,所以反比例函数y=的图象在第一,三象限内.
三、8.解:(1)因为y1与x成正比例,所以设y1=k1x(k1≠0);又因为y2与x成反比例,所以设y2=(k2≠0),所以y=y1-y2=k1x-.把x=1,y=0;x=2,y=3分别代入上式,得解得,所以y与x之间的函数关系式为y=2x-.(2)当x=6时,y=2×6-=11.
点拨:本题综合了正比例,反比例函数的关系式,二元一次方程组,代数式的求值等知识点,其中正确表示y与x之间的函数关系式是解本题的关键.
四、9.解:(1)由题图知:当每小时排水4立方米时,共需12小时排完蓄水池中的水,所以蓄水量为4×12=48(立方米).
(2)由题图可知V与t成反比例关系,所以设V=,把V=4,t=12代入得k=48,所以V=(t>0).当t=6时,V==8,即每小时的排水量应该是8立方米. 点拨:关键是能从图象中获取有用信息,会根据图象回答问题.
B卷
一、1.解:(1)由题意,得│m│-2=-1,解得m=1或m=-1.当m=1时,m-1=0,所以m=1应舍去;当m=-1时,m-1≠0,所以m=-1时,y=(m-1)x|m|-2为反比例函数.(2)y不可能是x的反比例函数,这是因为:当m-3=-1时,m=2,但当m=2时,m2-m-2=22-2-2=0,故原函数变为y=0,所以y不可能是x的反比例函数;y可能是x的正比例函数.这是因为:当m-3=1时,m=4,当m=4时,m2-m-2≠0,故当m=4时,y=(m2-m-2)xm-3是正比例函数.
点拨:以上各题的已知、结论都不相同,但是利用反比例函数y=kx-1中的k≠0及自变量指数为-1解题的思路是相同的.
2.解:设点A的坐标为(a,b),则S△AOB=ab=1,所以ab=2.因为点A(a,b)在双曲线y=上,所以k=ab=2.所以反比例函数的关系式为y=,一次函数关系式为y=2x-1.
(1)①由题意,得a·2a=4,所以a=4,所以a=2(a>0),所以点A的坐标为(2,4);②把点A的坐标分别代入y=k1x和y=中,得k1=2,k2=8,所以正比例函数和反比例函数的关系式分别为y=2x,y=.(2)设点A的坐标为(a,b),则B(-a,-b),BC=2a,AC=2b,由题意,得·2a·2b=4,所以ab=2.又因为点A(a,b)在函数y=的图象上,所以ab=k=2,所以反比例函数的关系式为y=.
二、3.解:当x=0时,y=-2x-2=-2.当y=0时,-2x-2=0,解得x=-1,所以直线y=-2x-2与x轴,y轴的交点分别为B(-1,0),C(0,-2),所以OB=1,OC=2,所以S△OBC=OB·OC=×1×2=1,因为S△ADB =S△OBC,所以S△ADB =1.设A的坐标为(m,n),则点D的坐标为(m,0),k=mn.所以OD=│m│=-m(m<0),AD=│n│=n(n>0),所以BD=OD-OB=-m-1.所以S△ADB =AD·BD=n(-m-1)=-(m+1)n=1.又因为点A(m,n)在直线y=-2x-2上,所以-2m-2=n,所以m=-.把m=-代入-(m+1)n=1中,得-(-+1)n=1,所以n2=4,解得n=±2,因为n>0,所以n=2,所以m==-2.所以k=mn=-4. 点拨:由点的坐标求线段的长度(比如OD的长)时,应注意坐标的符号,正确地求出线段的长度(如OD=-m,而不是OD=m).
三、4.解:设进货数量为a,进货价格为b,售出数量为c,售出价格为d,则y=,x=.因为商场希望通过该商品获取50%的利润,所以售出数量c乘以售出价格d,减去进货数量a乘以进货价格b,所得的差为进货数量a与进货价格b的积的一半.即:cd-ab=ab;两边同除以ab,得-1=,即xy-1=.所以商品的销售率y与价格倍数x之间的关系式为xy=,即y=,y是x的反比例函数.
四、5.A 点拨:2xy=20,所以y=,所以函数图象上的点的横,纵坐标的乘积为10,观察四个选项,A符合条件,B自变量的取值不对.C,D中图象上点的坐标符合要
6. A
7. D
8. B
C卷
一、1.解:(1)Rt△AOP的面积不会发生变化,因为S△AOP=│k│=;(2)>
点拨:第(2)问中S1=S△OBD,而S△OBD =S2+S△OPC,所以S1>S2.
二、2.解:(1);反比例 (2)观察题图象知当a=1时,h=5,所以2S=ha=5,所以S=,所以三角形的面积为.(3)h随a的增大而减小.
点拨:认真观察图象,获取正确的信息是解答此类题的关键.
三、3.解:y是x的反比例函数,令y=(k≠0),将x=-6,y=1代入y=,得k=xy=-6,所以y与x的函数关系式为y=-.(2)y=-的图象是双曲线,图象在第二,第四象限,并且在每一个象限内,y随x的增大而增大.
点拨:观察表格中的每一组数据,它们的积都等于-6,故判断y是x的反比例函数.
4.解:李明同学的解答过程有错误.李明同学忽略了实际问题中自变量x的取值范围.
点拨:反映实际问题的反比例函数,其自变量的取值不可能为负数,只可能是正数范围内的部分,因此,在画反比例函数的图象时,要在自变更的取值范围内画出其图象.
