17.1.2反比例函数的图象和性质(1) 课件(26张)
文档属性
| 名称 | 17.1.2反比例函数的图象和性质(1) 课件(26张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-06 09:13:07 | ||
图片预览





文档简介
(共26张PPT)
17.1.2 反比例函数的
图 象 和 性 质(1)
一、教学目标
1、进一步巩固复习作函数图象的一般方法和步骤
2、会画出反比例函数的图象,用类比的方法,数形结合的思想,对图形进行观察、分析和归纳,掌握反比例函数的图象和性质
一、挑战“记忆”
1、什么是反比例函数?
2、反比例函数的定义中还需要注意什么?
◆自变量x的取值范围
◆自变量x的次数为
-2
±1
x≠0
◆若函数y=(m-2)xm2-5是反比例函数,则m= ,
y=kx-1
xy=k
(k≠0)
在每个象限内
在每个象限内
y
X
O
k>0
K<0
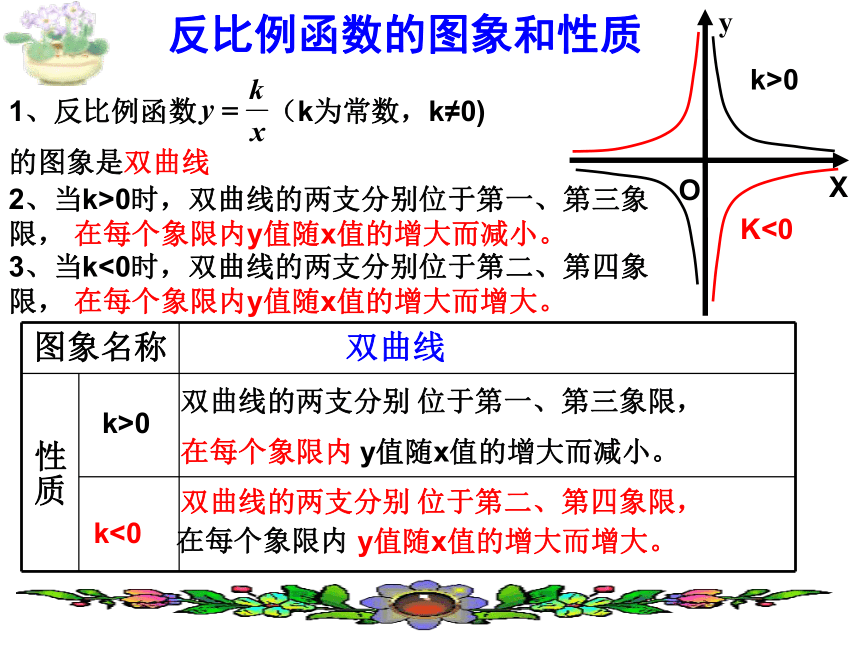
反比例函数的图象和性质
双曲线的两支分别
双曲线的两支分别
双曲线
k>0
k<0
位于第一、第三象限,
位于第二、第四象限,
y值随x值的增大而减小。
y值随x值的增大而增大。
1、反比例函数 (k为常数,k≠0)
的图象是双曲线
2、当k>0时,双曲线的两支分别位于第一、第三象限, 在每个象限内y值随x值的增大而减小。
3、当k<0时,双曲线的两支分别位于第二、第四象限, 在每个象限内y值随x值的增大而增大。
图象名称
性质
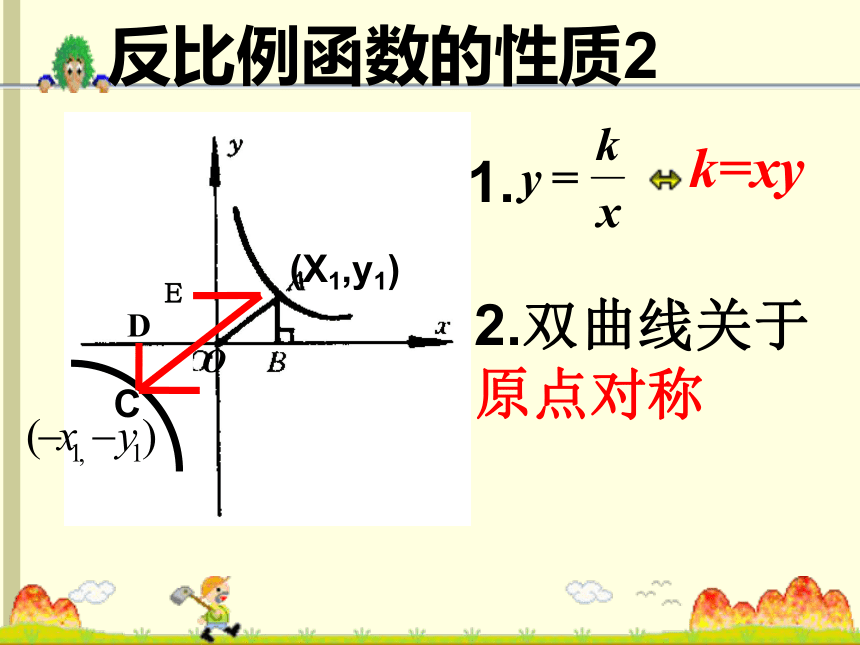
反比例函数中心对称及轴对称性质
反比例函数的性质2
(X1,y1)
O
2.双曲线关于原点对称
E
k=xy
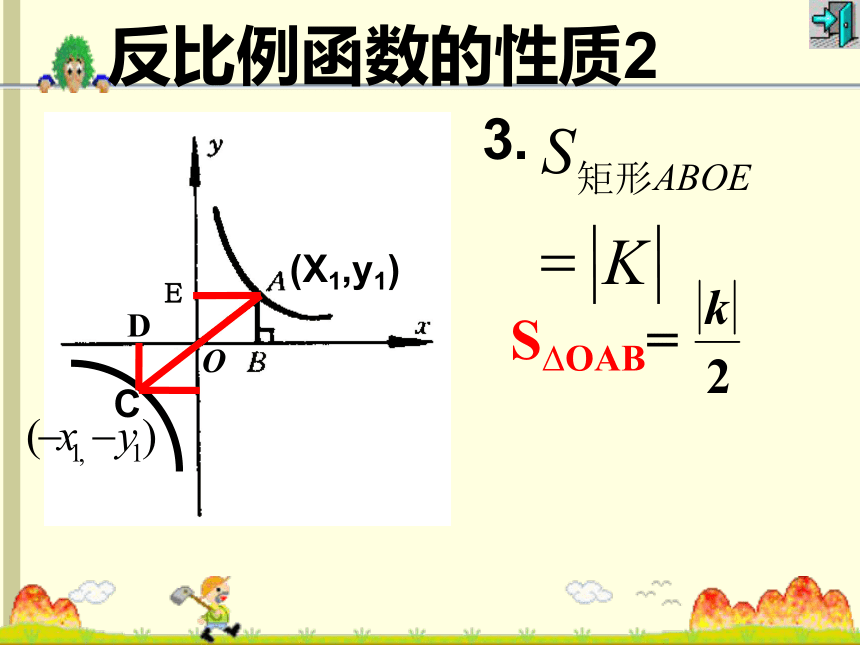
反比例函数的性质2
(X1,y1)
O
3.
E
S?OAB=
1.反比例函数
的图象位于第二、四象限,则m的值是 .
A.-2 B.-1
C.0或-1 D.-2或-1
练习1
B
D
1、函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
2、 函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
3、函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三
二、四
一
减小
增大
减小
已知反比例函数
若函数的图象位于第一三象限,
则k_____________;
若在每一象限内,y随x增大而增大,
则k_____________.
< 4
> 4
3.设点P1(x1,y1),P2(x2,y2)都在反比例函数 - 上,且x1).
练习4
<
若点(-2,y1)、(-1,y2)、(2,y3)在
反比例函数 的图象上,则( )
A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1
B
函数y=kx-k 与 在同一条直角坐标系中的 图象可能是 :
D
考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .
-1
-1x<-2或x>0
练习8
4.如图,Rt△AOB的顶点A在双曲线 上,且S△AOB=3,求m的值.
∵ S△AOB =1/2m=3
∴ m=6
9(2010·遵义中考)如图,在第一象限
内,点P,M(a,2)是双曲线y= (k≠0)上的
两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与
OM交于点C,则△OAC的面积为_____.
【解析】由图可得k=6,a=3,通过△OCA∽△OMB可求得△OAC的面积.
答案:
11.(12分)(2010·河北中考)如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数y= (x>0)的图象过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(3)若反比例函数y= (x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
【解】(1)设直线DE的解析式为y=kx+b,
∵点D,E的坐标为(0,3)、(6,0),
∴y=- x+3.
∵点M在AB边上,B(4,2),而四边形OABC是矩形,
∴点M的纵坐标为2.
又∵点M在直线y=- x+3上,
∴2=- x+3.∴x=2.
∴直线DE的解析式为y=- x+3,M(2,2).
(2)∵y= (x>0)经过点M(2,2),
∴m=4.∴y= .
又∵点N在BC边上,B(4,2),∴点N的横坐标为4.
∵点N在直线y=- x+3上,∴y=1.∴N(4,1).
∵当x=4时,y= =1,
∴点N在函数y= 的图象上.
(3)4≤ m ≤8.
已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).
C
1.通过本节课的学习,你有什么收获?还有什么困惑吗?
2.你对自己本节课的表现满意吗?为什么?
数缺形时少直觉,
形少数时难入微.
1、进一步巩固复习了作函数图象的一般方法和步骤
2、亲手画出函数的图象,用类比的方法,数形结合的思想,有了对图形进行观察、分析和归纳的体验,掌握了反比例函数的图象和性质
当k>0时,双曲线的两支分别位于第一、第三象限, 在每个象限内y值随x值的增大而减小。
当k<0时,双曲线的两支分别位于第二、第四象限, 在每个象限内y值随x值的增大而增大。
3、反比例函数 (k为常数,k≠0)的图象是双曲线
练 习
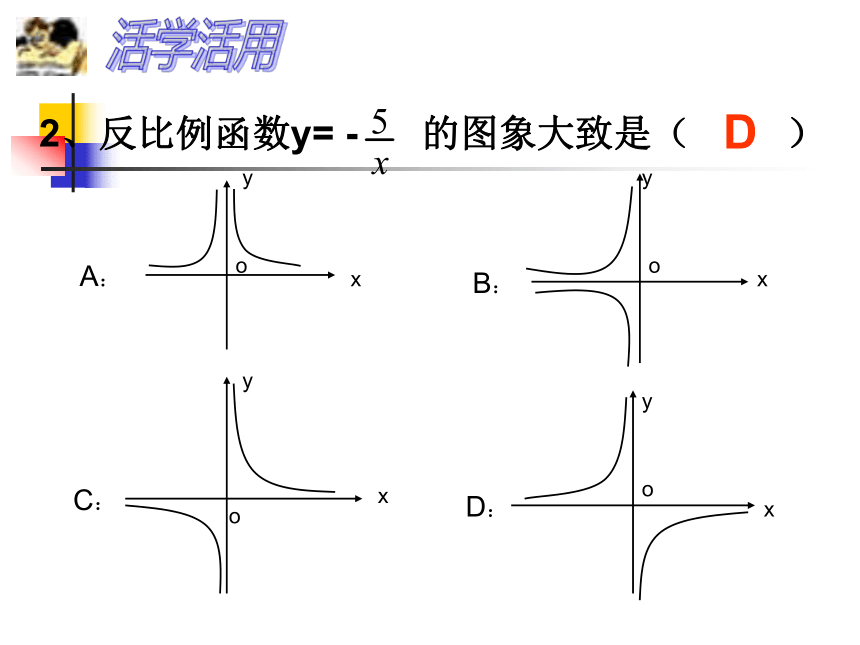
1. 已知k<0,则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )
2. 已知k>0,则函数 y1=kx+k与y2= 在同一坐标系中
的图象大致是 ( )
3.设x为一切实数,在下列函数中,当x减小时,y的值总是增大的函数是( )
(A) y = -5x -1 ( B)y =
(C)y=-2x+2; (D)y=4x.
D
C
C
17.1.2 反比例函数的
图 象 和 性 质(1)
一、教学目标
1、进一步巩固复习作函数图象的一般方法和步骤
2、会画出反比例函数的图象,用类比的方法,数形结合的思想,对图形进行观察、分析和归纳,掌握反比例函数的图象和性质
一、挑战“记忆”
1、什么是反比例函数?
2、反比例函数的定义中还需要注意什么?
◆自变量x的取值范围
◆自变量x的次数为
-2
±1
x≠0
◆若函数y=(m-2)xm2-5是反比例函数,则m= ,
y=kx-1
xy=k
(k≠0)
在每个象限内
在每个象限内
y
X
O
k>0
K<0
反比例函数的图象和性质
双曲线的两支分别
双曲线的两支分别
双曲线
k>0
k<0
位于第一、第三象限,
位于第二、第四象限,
y值随x值的增大而减小。
y值随x值的增大而增大。
1、反比例函数 (k为常数,k≠0)
的图象是双曲线
2、当k>0时,双曲线的两支分别位于第一、第三象限, 在每个象限内y值随x值的增大而减小。
3、当k<0时,双曲线的两支分别位于第二、第四象限, 在每个象限内y值随x值的增大而增大。
图象名称
性质
反比例函数中心对称及轴对称性质
反比例函数的性质2
(X1,y1)
O
2.双曲线关于原点对称
E
k=xy
反比例函数的性质2
(X1,y1)
O
3.
E
S?OAB=
1.反比例函数
的图象位于第二、四象限,则m的值是 .
A.-2 B.-1
C.0或-1 D.-2或-1
练习1
B
D
1、函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
2、 函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
3、函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三
二、四
一
减小
增大
减小
已知反比例函数
若函数的图象位于第一三象限,
则k_____________;
若在每一象限内,y随x增大而增大,
则k_____________.
< 4
> 4
3.设点P1(x1,y1),P2(x2,y2)都在反比例函数 - 上,且x1
练习4
<
若点(-2,y1)、(-1,y2)、(2,y3)在
反比例函数 的图象上,则( )
A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1
B
函数y=kx-k 与 在同一条直角坐标系中的 图象可能是 :
D
考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .
-1
-1
练习8
4.如图,Rt△AOB的顶点A在双曲线 上,且S△AOB=3,求m的值.
∵ S△AOB =1/2m=3
∴ m=6
9(2010·遵义中考)如图,在第一象限
内,点P,M(a,2)是双曲线y= (k≠0)上的
两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与
OM交于点C,则△OAC的面积为_____.
【解析】由图可得k=6,a=3,通过△OCA∽△OMB可求得△OAC的面积.
答案:
11.(12分)(2010·河北中考)如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数y= (x>0)的图象过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(3)若反比例函数y= (x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
【解】(1)设直线DE的解析式为y=kx+b,
∵点D,E的坐标为(0,3)、(6,0),
∴y=- x+3.
∵点M在AB边上,B(4,2),而四边形OABC是矩形,
∴点M的纵坐标为2.
又∵点M在直线y=- x+3上,
∴2=- x+3.∴x=2.
∴直线DE的解析式为y=- x+3,M(2,2).
(2)∵y= (x>0)经过点M(2,2),
∴m=4.∴y= .
又∵点N在BC边上,B(4,2),∴点N的横坐标为4.
∵点N在直线y=- x+3上,∴y=1.∴N(4,1).
∵当x=4时,y= =1,
∴点N在函数y= 的图象上.
(3)4≤ m ≤8.
已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是( ).
C
1.通过本节课的学习,你有什么收获?还有什么困惑吗?
2.你对自己本节课的表现满意吗?为什么?
数缺形时少直觉,
形少数时难入微.
1、进一步巩固复习了作函数图象的一般方法和步骤
2、亲手画出函数的图象,用类比的方法,数形结合的思想,有了对图形进行观察、分析和归纳的体验,掌握了反比例函数的图象和性质
当k>0时,双曲线的两支分别位于第一、第三象限, 在每个象限内y值随x值的增大而减小。
当k<0时,双曲线的两支分别位于第二、第四象限, 在每个象限内y值随x值的增大而增大。
3、反比例函数 (k为常数,k≠0)的图象是双曲线
练 习
1. 已知k<0,则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )
2. 已知k>0,则函数 y1=kx+k与y2= 在同一坐标系中
的图象大致是 ( )
3.设x为一切实数,在下列函数中,当x减小时,y的值总是增大的函数是( )
(A) y = -5x -1 ( B)y =
(C)y=-2x+2; (D)y=4x.
D
C
C
