新课标人教A版高中数学必修二《两点间的距离公式》课件(共23张ppt)
文档属性
| 名称 | 新课标人教A版高中数学必修二《两点间的距离公式》课件(共23张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 503.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-22 11:48:51 | ||
图片预览







文档简介
(共23张PPT)
【类比探究,生成新知】
|x1-x2|
1.旧知-铺垫
如图,若P1、P2是数轴上两点,则|P1P2|=_______.
0
P1
P2
x2
x1
0
P2
P1
x1
x2
x
o
y
1>当y1=y2时
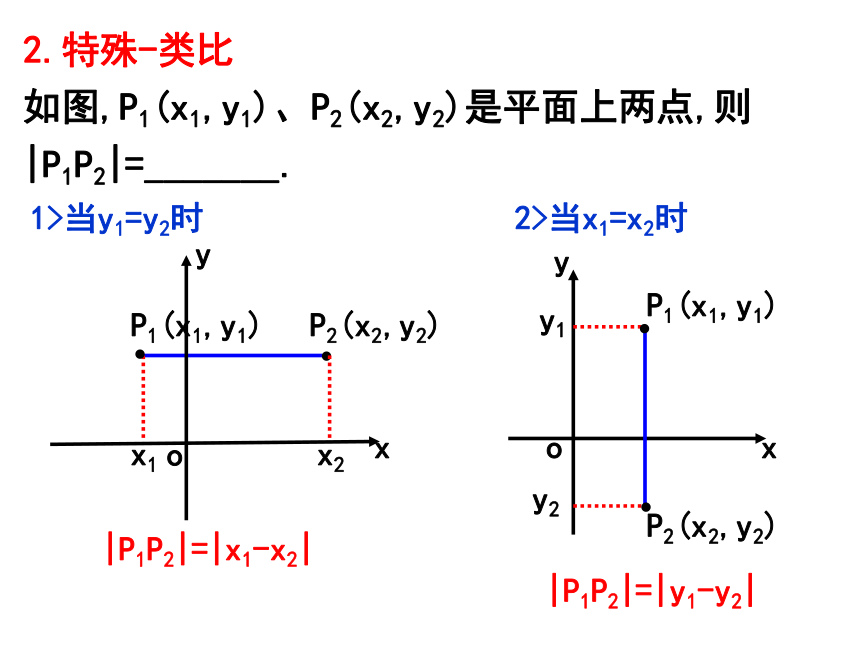
2.特殊-类比
如图,P1(x1,y1)、P2(x2,y2)是平面上两点,则|P1P2|=_______.
P1(x1,y1)
P2(x2,y2)
x1
x2
|P1P2|=|x1-x2|
2>当x1=x2时
y
x
o
P1(x1,y1)
P2(x2,y2)
y1
y2
|P1P2|=|y1-y2|
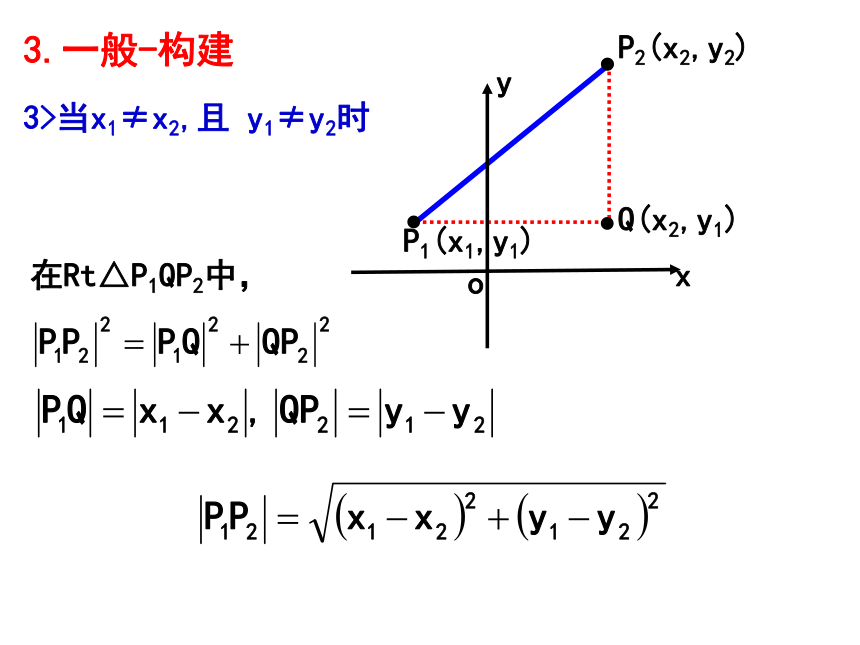
3.一般-构建
3>当x1≠x2,且 y1≠y2时
x
o
y
P1(x1,y1)
P2(x2,y2)
Q(x2,y1)
在Rt△P1QP2中,
2).原点o(0,0)与任意一点P(x,y)的距离为:
4.公式-理解
平面内P1(x1,y1)、P2(x2,y2)两点间的距离公式:
1).公式特征:
两点的横坐标之差与纵坐标之差的平方和的算术平方根.
【自主探究,掌握新知】
1.求下列两点间的距离:
(1).A(6,0)、 B(-2,0)
(2).C(0,-4)、 D(0,-1)
(3).E(0,0)、 F(3,4)
(4).G(2,1)、 H(5,-1)
一层练习:(用口答)
8
3
5
二层练习:(动手做)
2.若两点A(0,10),B(a,-5)的距离为17,则
a=_____;
±8
三层练习:(用脑想)
3.已知△ABC的三个顶点A(1,2)、 B(3,4)、C(5,0),则ABC的形状为( ).
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
A
【合作探究,运用新知】
例1.已知点A(-1,2)、B(2, ),在x轴上求一点P,使|PA|=|PB|,并求|PA|的值.
解法一:设所求点为P(x,0),于是有
解得x=1,所以所求点P(1,0)
方程思想
解法二:
利用几何性质
x
o
y
B
A
P
例1.已知点A(-1,2)、B(2, ),在x轴上求一点P,使|PA|=|PB|,并求|PA|的值.
法一
M
<数学与生活1>
B
A
P
郊 外
郊 外
高尔夫球场
问题:爸爸在A地,妈妈在B地,如图。你会将小家建在郊外的哪一个地方?
生活:儒家中庸,
做人之道.
数学:|PA|=|PB|.
A:爸爸
B:妈妈
1.已知点A(-1,-2)、B(2,3),在x轴上求一点P,使d=|PA|+|PB|取最小值,并求出最小值.
变式训练1:
x
o
y
B
P
A
P
【交流探究,拓展新知】
<学有所获2>
若A、B两点在直线l的异侧,则直线AB与直线l的交点为所求的点P,且最短距离为|AB|。(本质:两点之间,直线段最短。)
<数学与生活2>
B
A
P
郊 外
郊 外
问题:如果你打算从A地去B地旅行,途经郊外,如图.你将会怎样走用时最省?
生活:两点之间,直线段最短,
时间最省.
数学:d=|AP|+|PB|取最小值.
2.已知点A(-1,2)、B(2,3),在x轴上求一点P,使d=|PA|+|PB|取最小值.
变式训练2:
x
o
y
A
B
P
A1
P
勇于尝试
变式训练3:
<学有所获3>
若A、B两点在目标直线l的同侧,只需找其中一点关于直线l的对称点(如A点的对称点A1),则|A1B|为所求的最短距离,直线A1B与直线l的交点为所求的点P。(本质:三角形中两边之和大于第三边。)
<数学与生活3>
B
A
P
郊 外
郊 外
问题:若要修建两条高速公路PA、PB,如图,如果你是公路的承建商,你将会怎样设计呢?
生活:成本最低,
生财之道.
数学:d=|PA|+|PB|取最小值.
3.已知函数f(x)= ,
求函数f(x)的最小值.
变式训练3:
源于联想
结构特征
距离公式
转化化归
解决问题
函数f(x)表示点P(x,0)与A(-1,-2)、B(2,3)的距离之和。
变式训练1:
变式训练2:
<学有所获4>
结构决定思路,思路决定出路;
注重方程、转化、数形结合等数学思想。
【自我归纳,完善总结】
1.知识归纳:
2.方法归纳:
注重方程、转化、数形结合等数学思想。
【作业布置,分层完成】
1.必做题: P109(A)6,7,8
2.选做题: (B)7
【课外探究,激发潜能】
1.已知点A(-1,2)、B(2,3),在x轴上求一点P,使 d=||PA|-|PB||取最大值,并求出最大值.
2.已知直线l:2x-y+1=0和点O(0,0)、M(0,3),试在l上求一点P,使d=||P0|-|PM||取最大值,并求出最大值.
【类比探究,生成新知】
|x1-x2|
1.旧知-铺垫
如图,若P1、P2是数轴上两点,则|P1P2|=_______.
0
P1
P2
x2
x1
0
P2
P1
x1
x2
x
o
y
1>当y1=y2时
2.特殊-类比
如图,P1(x1,y1)、P2(x2,y2)是平面上两点,则|P1P2|=_______.
P1(x1,y1)
P2(x2,y2)
x1
x2
|P1P2|=|x1-x2|
2>当x1=x2时
y
x
o
P1(x1,y1)
P2(x2,y2)
y1
y2
|P1P2|=|y1-y2|
3.一般-构建
3>当x1≠x2,且 y1≠y2时
x
o
y
P1(x1,y1)
P2(x2,y2)
Q(x2,y1)
在Rt△P1QP2中,
2).原点o(0,0)与任意一点P(x,y)的距离为:
4.公式-理解
平面内P1(x1,y1)、P2(x2,y2)两点间的距离公式:
1).公式特征:
两点的横坐标之差与纵坐标之差的平方和的算术平方根.
【自主探究,掌握新知】
1.求下列两点间的距离:
(1).A(6,0)、 B(-2,0)
(2).C(0,-4)、 D(0,-1)
(3).E(0,0)、 F(3,4)
(4).G(2,1)、 H(5,-1)
一层练习:(用口答)
8
3
5
二层练习:(动手做)
2.若两点A(0,10),B(a,-5)的距离为17,则
a=_____;
±8
三层练习:(用脑想)
3.已知△ABC的三个顶点A(1,2)、 B(3,4)、C(5,0),则ABC的形状为( ).
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
A
【合作探究,运用新知】
例1.已知点A(-1,2)、B(2, ),在x轴上求一点P,使|PA|=|PB|,并求|PA|的值.
解法一:设所求点为P(x,0),于是有
解得x=1,所以所求点P(1,0)
方程思想
解法二:
利用几何性质
x
o
y
B
A
P
例1.已知点A(-1,2)、B(2, ),在x轴上求一点P,使|PA|=|PB|,并求|PA|的值.
法一
M
<数学与生活1>
B
A
P
郊 外
郊 外
高尔夫球场
问题:爸爸在A地,妈妈在B地,如图。你会将小家建在郊外的哪一个地方?
生活:儒家中庸,
做人之道.
数学:|PA|=|PB|.
A:爸爸
B:妈妈
1.已知点A(-1,-2)、B(2,3),在x轴上求一点P,使d=|PA|+|PB|取最小值,并求出最小值.
变式训练1:
x
o
y
B
P
A
P
【交流探究,拓展新知】
<学有所获2>
若A、B两点在直线l的异侧,则直线AB与直线l的交点为所求的点P,且最短距离为|AB|。(本质:两点之间,直线段最短。)
<数学与生活2>
B
A
P
郊 外
郊 外
问题:如果你打算从A地去B地旅行,途经郊外,如图.你将会怎样走用时最省?
生活:两点之间,直线段最短,
时间最省.
数学:d=|AP|+|PB|取最小值.
2.已知点A(-1,2)、B(2,3),在x轴上求一点P,使d=|PA|+|PB|取最小值.
变式训练2:
x
o
y
A
B
P
A1
P
勇于尝试
变式训练3:
<学有所获3>
若A、B两点在目标直线l的同侧,只需找其中一点关于直线l的对称点(如A点的对称点A1),则|A1B|为所求的最短距离,直线A1B与直线l的交点为所求的点P。(本质:三角形中两边之和大于第三边。)
<数学与生活3>
B
A
P
郊 外
郊 外
问题:若要修建两条高速公路PA、PB,如图,如果你是公路的承建商,你将会怎样设计呢?
生活:成本最低,
生财之道.
数学:d=|PA|+|PB|取最小值.
3.已知函数f(x)= ,
求函数f(x)的最小值.
变式训练3:
源于联想
结构特征
距离公式
转化化归
解决问题
函数f(x)表示点P(x,0)与A(-1,-2)、B(2,3)的距离之和。
变式训练1:
变式训练2:
<学有所获4>
结构决定思路,思路决定出路;
注重方程、转化、数形结合等数学思想。
【自我归纳,完善总结】
1.知识归纳:
2.方法归纳:
注重方程、转化、数形结合等数学思想。
【作业布置,分层完成】
1.必做题: P109(A)6,7,8
2.选做题: (B)7
【课外探究,激发潜能】
1.已知点A(-1,2)、B(2,3),在x轴上求一点P,使 d=||PA|-|PB||取最大值,并求出最大值.
2.已知直线l:2x-y+1=0和点O(0,0)、M(0,3),试在l上求一点P,使d=||P0|-|PM||取最大值,并求出最大值.
