苏科版八年级数学下册期中巩固专题一:利用轴对称求最短路径题型汇总学案(含答案)
文档属性
| 名称 | 苏科版八年级数学下册期中巩固专题一:利用轴对称求最短路径题型汇总学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 229.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-20 00:00:00 | ||
图片预览



文档简介
八下春季班期中专题巩固一:利用轴对称求最短路径题型汇总
轴对称的作用是“搬点移线”,可以把图形中比较分散、缺乏联系的元素集中到“新的图形”中,为应用某些基本定理提供方便。比如我们可以利用轴对称性质求几何图形中一些线段和的最大值或最小值问题。
利用轴对称的性质解决几何图形中的最值问题借助的主要基本定理有3个:
(1)两点之间线段最短;
(2)三角形两边之和大于第三边;
(3)垂线段最短。
初中阶段利用轴对称性质求最值的题目可以归结为:两点一线,两点两线,一点两线三类线段和的最值问题
两点一线的最值问题: (两个定点 + 一个动点)
问题特征:已知两个定点位于一条直线的同一侧,在直线上求一动点的位置,使动点与定点线段和最短。
核心思路:这类最值问题所求的线段和中只有一个动点,解决这类题目的方法是找出任一定点关于动点所在直线的对称点,连结这个对称点与另一定点,交动点所在直线于一点,交点即为动点满足最值的位置。
方法:1.定点过动点所在直线做对称。
2.连结对称点与另一个定点,则直线段长度就是我们所求。
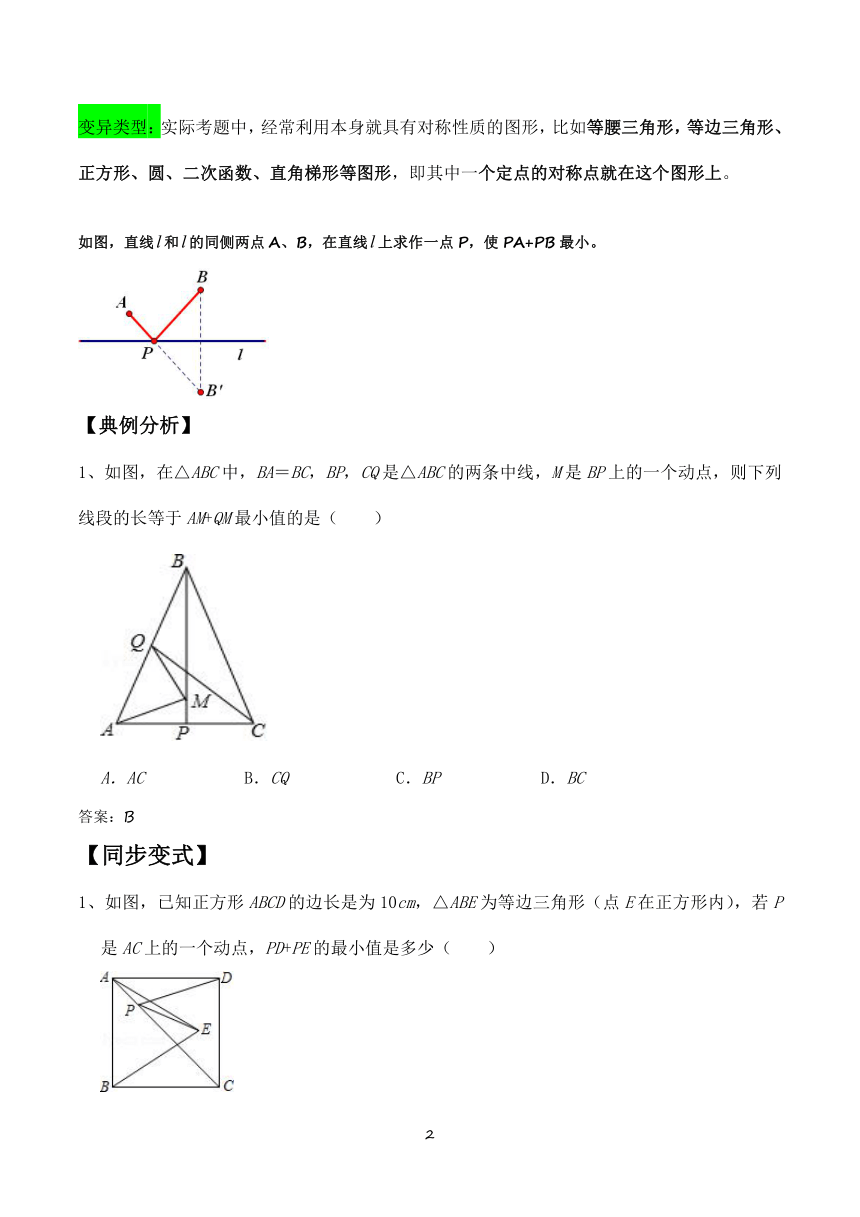
变异类型:实际考题中,经常利用本身就具有对称性质的图形,比如等腰三角形,等边三角形、正方形、圆、二次函数、直角梯形等图形,即其中一个定点的对称点就在这个图形上。
如图,直线和的同侧两点A、B,在直线上求作一点P,使PA+PB最小。
【典例分析】
1、如图,在△ABC中,BA=BC,BP,CQ是△ABC的两条中线,M是BP上的一个动点,则下列线段的长等于AM+QM最小值的是( )
AC B.CQ C.BP D.BC
答案:B
【同步变式】
1、如图,已知正方形ABCD的边长是为10cm,△ABE为等边三角形(点E在正方形内),若P是AC上的一个动点,PD+PE的最小值是多少( )
A.6cm B.8cm C.10cm D.5cm
答案:C
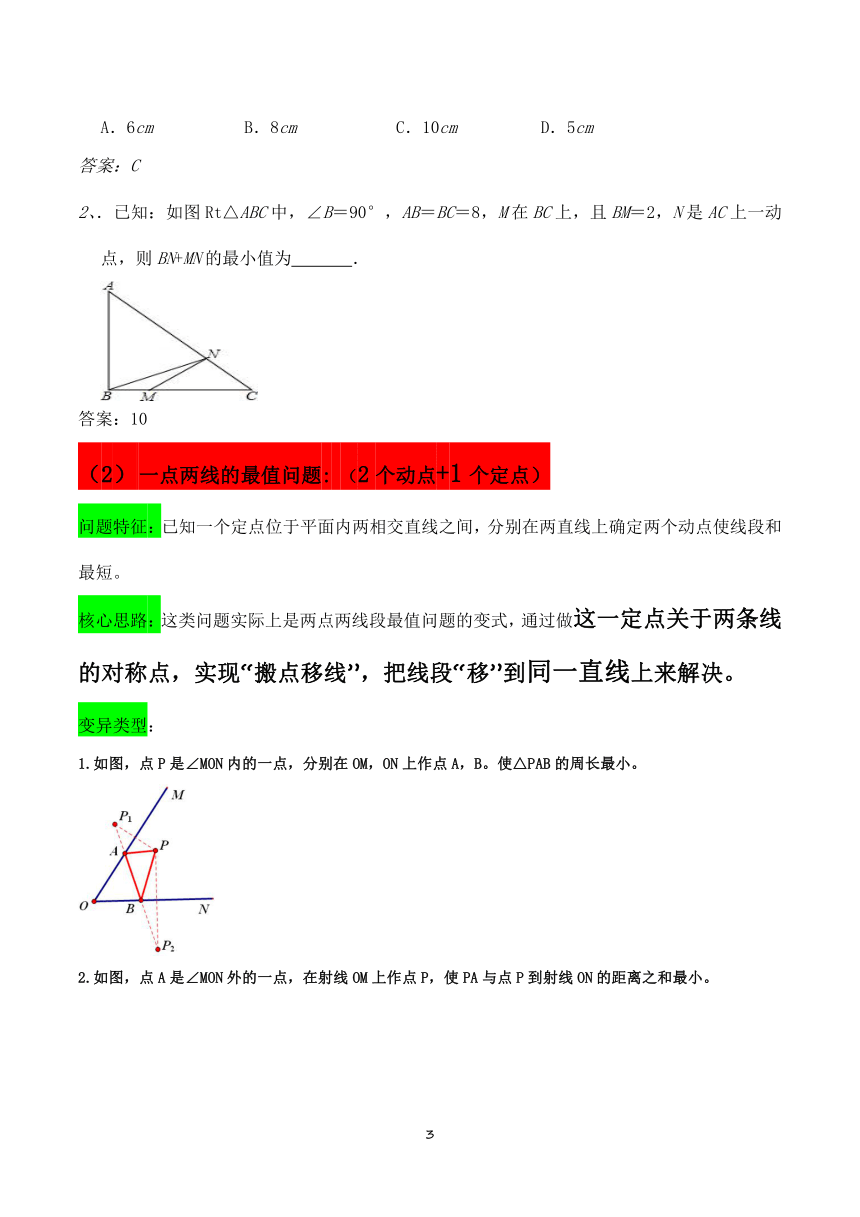
2、.已知:如图Rt△ABC中,∠B=90°,AB=BC=8,M在BC上,且BM=2,N是AC上一动点,则BN+MN的最小值为 .
答案:10
一点两线的最值问题: (2个动点+1个定点)
问题特征:已知一个定点位于平面内两相交直线之间,分别在两直线上确定两个动点使线段和最短。
核心思路:这类问题实际上是两点两线段最值问题的变式,通过做这一定点关于两条线的对称点,实现“搬点移线”,把线段“移”到同一直线上来解决。
变异类型:
1.如图,点P是∠MON内的一点,分别在OM,ON上作点A,B。使△PAB的周长最小。
2.如图,点A是∠MON外的一点,在射线OM上作点P,使PA与点P到射线ON的距离之和最小。
【典例分析】
1、在△ABC中,∠A=40°,点D在BC边上(不与C、D点重合),点P、点Q分别是AC、AB边上的动点,当△DPQ的周长最小时,则∠PDQ的度数为( )
A.140° B.120° C.100° D.70°
答案:C
2、.已知平面直角坐标系中,A,B两点的坐标分别为A(1,﹣2),B(3,﹣1),P,Q分别为x轴,y轴上的两个动点,则四边形AQPB周长的最小值为( )
A.5 B.5+ C.+ D.
答案:B
【同步变式】
1、如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为 .
答案:140°
2、.如图,在正方形ABCD中,E、F分别是AD、BC的中点,AG=AB,若AB=5,则下列结论:①EG⊥AF;②PF=2;③S△APB=S△APE;④若M是正方形内任一点,当S△AMB=S△APB时,△AMB的周长的最小值为5+;其中正确的结论是( )
①②③ B.①②④ C.①③④ D.①②③④
答案:D
两点两线的最值问题: (2个动点+2个定点)
问题特征:两动点,其中一个随另一个动(一个主动,一个从动),并且两动点间的距离保持不变。
核心思路:用平移方法,可把两动点变成一个动点,转化为“两个定点和一个动点”类型来解。
变异类型:
1.如图,点P,Q为∠MON内的两点,分别在OM,ON上作点A,B。使四边形PAQB的周长最小。
【典例分析】
如图,已知A(1,3),B(5,1),长度为2的线段PQ在x轴上平行移动,当AP+PQ+QB的值最小时,点P的坐标为
答案:(0,2)
【同步变式】
1、如图,在边长为1正方形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点,3AE=EB,有一只蚂蚁从E点出发,经过F、G、H,最后回点E点,则蚂蚁所走的最小路程是( )
A.2 B.4 C. D.
答案:C
两点两线的最值问题: (两个动点+两个定点)
问题特征:两动点分别在两条直线上独立运动,一动点分别到一定点和另一动点的距离和最小。
核心思路:利用轴对称变换,使一动点在另一动点的对称点与定点的线段上(两点之间线段最短),且这条线段垂直于另一动点的对称点所在直线(连接直线外一点与直线上各点的所有线段中,垂线段最短)时,两线段和最小,最小值等于这条垂线段的长。
变异类型:演变为多边形周长、折线段等最值问题。
1. 如图,点A是∠MON内的一点,在射线ON上作点P,使PA与点P到射线OM的距离之和最小。
【典例分析】
如图,已知P(3,2),B(﹣2,0),点Q从P点出发,先移动到y轴上的点M处,再沿垂直于y轴的方向向左移动1个单位至点N处,最后移动到点B处停止,当点Q移动的路径最短时(即三条线段PM、MN、NB长度之和最小),点M的坐标为( )
(0,) B.(0,) C.(0,) D.(0,)
答案:A
【同步变式】
如图1,在△ABC中,AB=BC=10,高AH=8.D是线段AC的动点,射线BD交AH于E点.
(1)若D恰好是AC的中点.
①求证:AC=BD;②求线段AE的长;
(2)如图2,作AM⊥BD于M,CN⊥BD于N,求AM+CN的最大值和最小值.
答案:(1)由勾股定理得BH=6,所以CH=4,再由勾股定理得AC=4,利用面积法求得AC=BD
。AE=5
(2)由等积法可以求出AM+CN的最小值为4,最大值为2
【课后练习】
1、三角形
1.如图,在等边△ABC中,AB=6,AD⊥BC,E是AC上的一点,M是AD上的一点,且AE=2,求EM+EC的最小值。
2.如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是____。
3.如图,△ABC中,AB=4,∠BAC=30°,若在AC、AB上各取一点M、N,使BM+MN的值最小,则这个最小值。
2、正方形
4.如图,正方形ABCD的边长为8,M在DC上,丐DM=2,N是AC上的一动点,DN+MN的最小值为_________。 即在直线AC上求一点N,使DN+MN最小 。
5.如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A. B. C.3 D.
3、矩形
6.如图,若四边形 ABCD 是矩形, AB = 10cm,BC = 20cm,E 为边 BC 上的一个动点,P 为 BD 上的一个动点,求 PC+PE的最小值;
【课后练习参考答案】
1、2
2、4
3、2
4、10
A
1
轴对称的作用是“搬点移线”,可以把图形中比较分散、缺乏联系的元素集中到“新的图形”中,为应用某些基本定理提供方便。比如我们可以利用轴对称性质求几何图形中一些线段和的最大值或最小值问题。
利用轴对称的性质解决几何图形中的最值问题借助的主要基本定理有3个:
(1)两点之间线段最短;
(2)三角形两边之和大于第三边;
(3)垂线段最短。
初中阶段利用轴对称性质求最值的题目可以归结为:两点一线,两点两线,一点两线三类线段和的最值问题
两点一线的最值问题: (两个定点 + 一个动点)
问题特征:已知两个定点位于一条直线的同一侧,在直线上求一动点的位置,使动点与定点线段和最短。
核心思路:这类最值问题所求的线段和中只有一个动点,解决这类题目的方法是找出任一定点关于动点所在直线的对称点,连结这个对称点与另一定点,交动点所在直线于一点,交点即为动点满足最值的位置。
方法:1.定点过动点所在直线做对称。
2.连结对称点与另一个定点,则直线段长度就是我们所求。
变异类型:实际考题中,经常利用本身就具有对称性质的图形,比如等腰三角形,等边三角形、正方形、圆、二次函数、直角梯形等图形,即其中一个定点的对称点就在这个图形上。
如图,直线和的同侧两点A、B,在直线上求作一点P,使PA+PB最小。
【典例分析】
1、如图,在△ABC中,BA=BC,BP,CQ是△ABC的两条中线,M是BP上的一个动点,则下列线段的长等于AM+QM最小值的是( )
AC B.CQ C.BP D.BC
答案:B
【同步变式】
1、如图,已知正方形ABCD的边长是为10cm,△ABE为等边三角形(点E在正方形内),若P是AC上的一个动点,PD+PE的最小值是多少( )
A.6cm B.8cm C.10cm D.5cm
答案:C
2、.已知:如图Rt△ABC中,∠B=90°,AB=BC=8,M在BC上,且BM=2,N是AC上一动点,则BN+MN的最小值为 .
答案:10
一点两线的最值问题: (2个动点+1个定点)
问题特征:已知一个定点位于平面内两相交直线之间,分别在两直线上确定两个动点使线段和最短。
核心思路:这类问题实际上是两点两线段最值问题的变式,通过做这一定点关于两条线的对称点,实现“搬点移线”,把线段“移”到同一直线上来解决。
变异类型:
1.如图,点P是∠MON内的一点,分别在OM,ON上作点A,B。使△PAB的周长最小。
2.如图,点A是∠MON外的一点,在射线OM上作点P,使PA与点P到射线ON的距离之和最小。
【典例分析】
1、在△ABC中,∠A=40°,点D在BC边上(不与C、D点重合),点P、点Q分别是AC、AB边上的动点,当△DPQ的周长最小时,则∠PDQ的度数为( )
A.140° B.120° C.100° D.70°
答案:C
2、.已知平面直角坐标系中,A,B两点的坐标分别为A(1,﹣2),B(3,﹣1),P,Q分别为x轴,y轴上的两个动点,则四边形AQPB周长的最小值为( )
A.5 B.5+ C.+ D.
答案:B
【同步变式】
1、如图,四边形ABCD中,∠BAD=110°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为 .
答案:140°
2、.如图,在正方形ABCD中,E、F分别是AD、BC的中点,AG=AB,若AB=5,则下列结论:①EG⊥AF;②PF=2;③S△APB=S△APE;④若M是正方形内任一点,当S△AMB=S△APB时,△AMB的周长的最小值为5+;其中正确的结论是( )
①②③ B.①②④ C.①③④ D.①②③④
答案:D
两点两线的最值问题: (2个动点+2个定点)
问题特征:两动点,其中一个随另一个动(一个主动,一个从动),并且两动点间的距离保持不变。
核心思路:用平移方法,可把两动点变成一个动点,转化为“两个定点和一个动点”类型来解。
变异类型:
1.如图,点P,Q为∠MON内的两点,分别在OM,ON上作点A,B。使四边形PAQB的周长最小。
【典例分析】
如图,已知A(1,3),B(5,1),长度为2的线段PQ在x轴上平行移动,当AP+PQ+QB的值最小时,点P的坐标为
答案:(0,2)
【同步变式】
1、如图,在边长为1正方形ABCD中,E、F、G、H分别是AB、BC、CD、DA上的点,3AE=EB,有一只蚂蚁从E点出发,经过F、G、H,最后回点E点,则蚂蚁所走的最小路程是( )
A.2 B.4 C. D.
答案:C
两点两线的最值问题: (两个动点+两个定点)
问题特征:两动点分别在两条直线上独立运动,一动点分别到一定点和另一动点的距离和最小。
核心思路:利用轴对称变换,使一动点在另一动点的对称点与定点的线段上(两点之间线段最短),且这条线段垂直于另一动点的对称点所在直线(连接直线外一点与直线上各点的所有线段中,垂线段最短)时,两线段和最小,最小值等于这条垂线段的长。
变异类型:演变为多边形周长、折线段等最值问题。
1. 如图,点A是∠MON内的一点,在射线ON上作点P,使PA与点P到射线OM的距离之和最小。
【典例分析】
如图,已知P(3,2),B(﹣2,0),点Q从P点出发,先移动到y轴上的点M处,再沿垂直于y轴的方向向左移动1个单位至点N处,最后移动到点B处停止,当点Q移动的路径最短时(即三条线段PM、MN、NB长度之和最小),点M的坐标为( )
(0,) B.(0,) C.(0,) D.(0,)
答案:A
【同步变式】
如图1,在△ABC中,AB=BC=10,高AH=8.D是线段AC的动点,射线BD交AH于E点.
(1)若D恰好是AC的中点.
①求证:AC=BD;②求线段AE的长;
(2)如图2,作AM⊥BD于M,CN⊥BD于N,求AM+CN的最大值和最小值.
答案:(1)由勾股定理得BH=6,所以CH=4,再由勾股定理得AC=4,利用面积法求得AC=BD
。AE=5
(2)由等积法可以求出AM+CN的最小值为4,最大值为2
【课后练习】
1、三角形
1.如图,在等边△ABC中,AB=6,AD⊥BC,E是AC上的一点,M是AD上的一点,且AE=2,求EM+EC的最小值。
2.如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是____。
3.如图,△ABC中,AB=4,∠BAC=30°,若在AC、AB上各取一点M、N,使BM+MN的值最小,则这个最小值。
2、正方形
4.如图,正方形ABCD的边长为8,M在DC上,丐DM=2,N是AC上的一动点,DN+MN的最小值为_________。 即在直线AC上求一点N,使DN+MN最小 。
5.如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A. B. C.3 D.
3、矩形
6.如图,若四边形 ABCD 是矩形, AB = 10cm,BC = 20cm,E 为边 BC 上的一个动点,P 为 BD 上的一个动点,求 PC+PE的最小值;
【课后练习参考答案】
1、2
2、4
3、2
4、10
A
1
同课章节目录
