苏科版八年级上册数学第1章全等三角形的复习学案(一):定义、性质与判定(无答案)
文档属性
| 名称 | 苏科版八年级上册数学第1章全等三角形的复习学案(一):定义、性质与判定(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-21 22:16:52 | ||
图片预览

文档简介
全等三角形的复习(一):定义、性质及判定条件
知识点回顾
定义
全等图形:
全等三角形:
全等符号 :
△ABC≌△DEF读作:
2、全等三角形的性质:
①全等三角形的对应边相等;全等三角形的对应角相等。
②全等三角形的周长、面积相等。
③全等三角形的对应边上的高对应相等。
④全等三角形的对应角的角平分线相等。
⑤全等三角形的对应边上的中线相等。
3、全等三角形的判定条件
边:
角:
4. 证明三角形全等的思路
5. 隐含条件
判定两个三角形全等,寻找条件时,应该注意图形中的隐含条件,常见的有:(1)公共边或公共角相等;(2)对顶角相等;(3)等边加(或减)等边,其和(或其差)仍相等;(4)等角加(或减)等角,其和(或差)仍相等;(5)同角或等角的余角(或补角)相等;(6)有中线或角平分线的定义得出线段或角相等;(7)由垂直定义得出直角相等。另外,一些自然规律如:“太阳光线可以看成是平行的”,“光的反射角等于入射角”等也是常用的隐含条件。
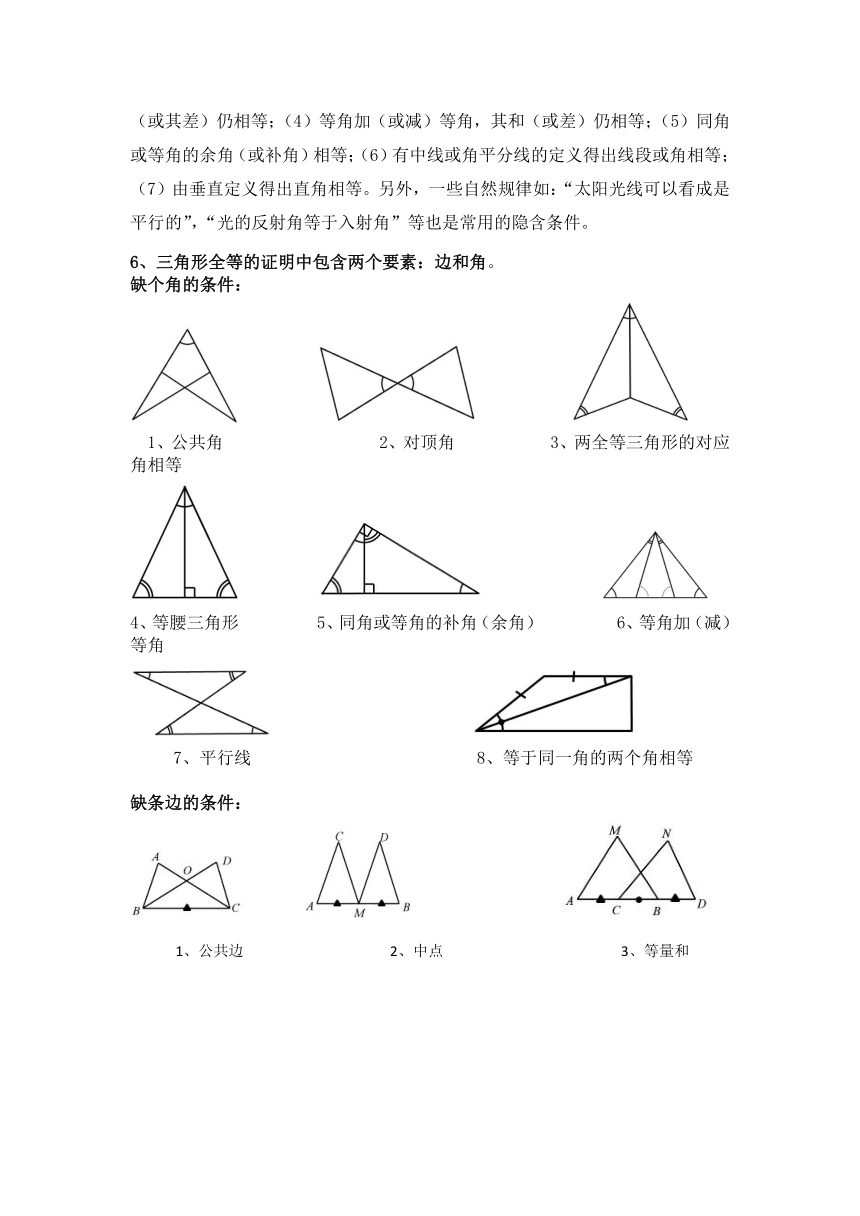
6、三角形全等的证明中包含两个要素:边和角。
缺个角的条件:
1、公共角 2、对顶角 3、两全等三角形的对应角相等
4、等腰三角形 5、同角或等角的补角(余角) 6、等角加(减)等角
7、平行线 8、等于同一角的两个角相等
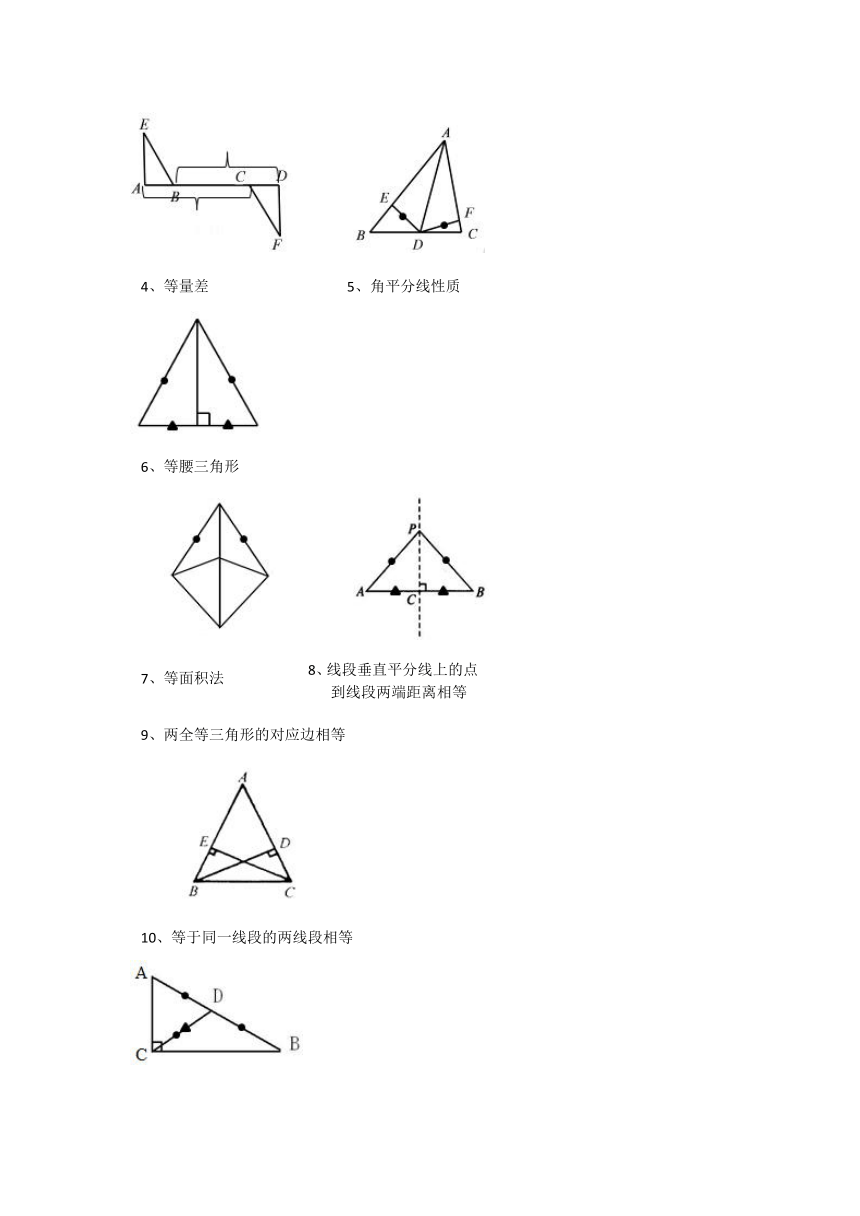
缺条边的条件:
【例题讲解】
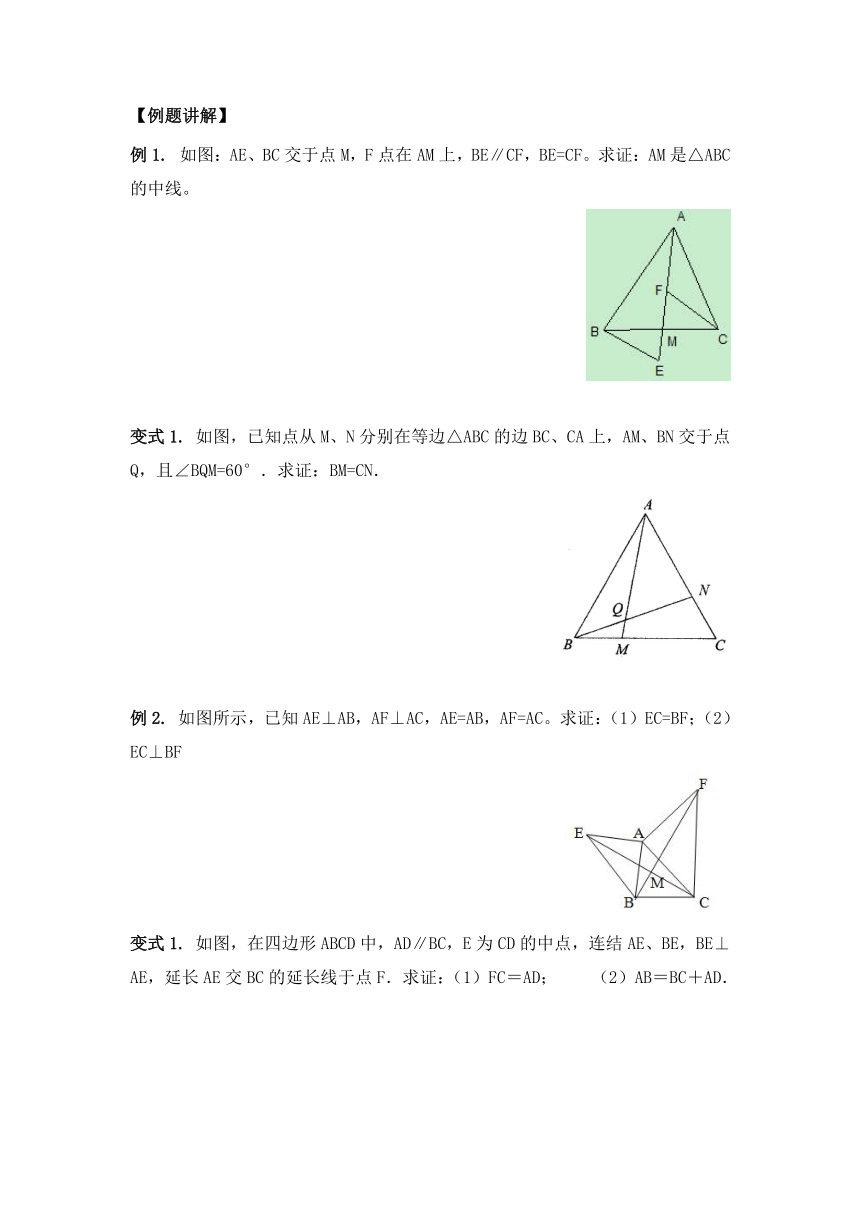
例1. 如图:AE、BC交于点M,F点在AM上,BE∥CF,BE=CF。求证:AM是△ABC的中线。
变式1. 如图,已知点从M、N分别在等边△ABC的边BC、CA上,AM、BN交于点Q,且∠BQM=60°.求证:BM=CN.
例2. 如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC。求证:(1)EC=BF;(2)EC⊥BF
变式1. 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连结AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:(1)FC=AD; (2)AB=BC+AD.
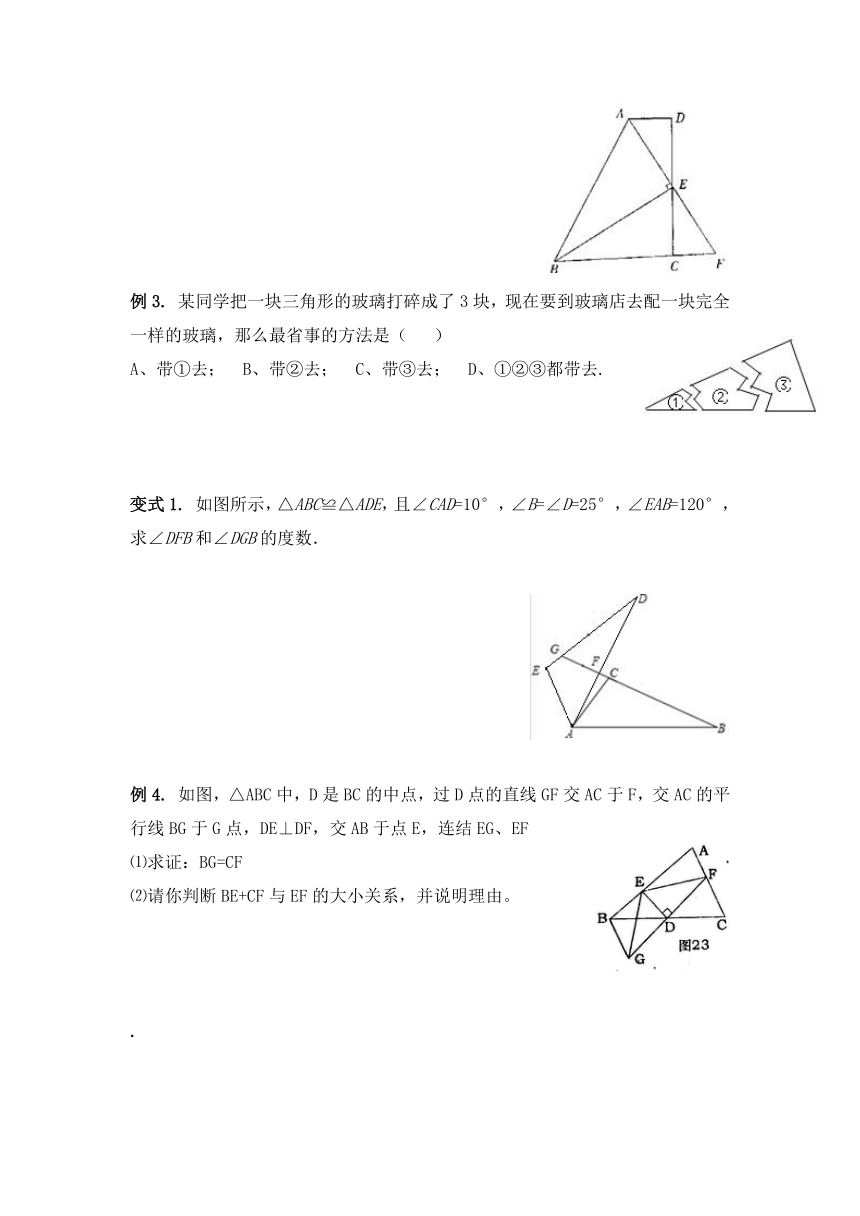
例3. 某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( )
A、带①去; B、带②去; C、带③去; D、①②③都带去.
变式1. 如图所示,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
例4. 如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF
⑴求证:BG=CF
⑵请你判断BE+CF与EF的大小关系,并说明理由。
.
变式1. 如图,已知AE=DE,AE⊥DE,AB⊥BC,DC⊥BC,求证:AB+CD=BC。
变式2. 已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.
(1)如图1,求证:△ACE≌△DCB.
(2)如图1,若∠ACD=60°,则∠AFB= ;如图2,若∠ACD=90°,则∠AFB= ;
(3)如图3,若∠ACD=β,则∠AFB= (用含β的式子表示)并说明理由.
随堂演练
1、如图,∠ACB=∠ADB=90°,AC=BD,AC、BD相交于O点,则(1)AD=BC; (2)∠DBC=∠CAD; (3)AO=BO; (4)AB‖CD。其中正确式子的序号有_____________。
第1题 第2题
2、在△ABC中,AB=AC,D、E两点在BC上,且有AD=AE,BD=CE,若∠BAD=30°,∠DAE=50°,则∠BAC的度数为()
A.130°? B.120°? C.110°? D.100°?
3、已知图中的两个三角形全等,则的度数是( )
A.72° B.60° C.58° D.50°
4、在与中,已有条件,还需添加两个条件才能使,不能添加的一组条件是()
A.,
B.,
C.,
D.,
12、如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC于点G
知识点回顾
定义
全等图形:
全等三角形:
全等符号 :
△ABC≌△DEF读作:
2、全等三角形的性质:
①全等三角形的对应边相等;全等三角形的对应角相等。
②全等三角形的周长、面积相等。
③全等三角形的对应边上的高对应相等。
④全等三角形的对应角的角平分线相等。
⑤全等三角形的对应边上的中线相等。
3、全等三角形的判定条件
边:
角:
4. 证明三角形全等的思路
5. 隐含条件
判定两个三角形全等,寻找条件时,应该注意图形中的隐含条件,常见的有:(1)公共边或公共角相等;(2)对顶角相等;(3)等边加(或减)等边,其和(或其差)仍相等;(4)等角加(或减)等角,其和(或差)仍相等;(5)同角或等角的余角(或补角)相等;(6)有中线或角平分线的定义得出线段或角相等;(7)由垂直定义得出直角相等。另外,一些自然规律如:“太阳光线可以看成是平行的”,“光的反射角等于入射角”等也是常用的隐含条件。
6、三角形全等的证明中包含两个要素:边和角。
缺个角的条件:
1、公共角 2、对顶角 3、两全等三角形的对应角相等
4、等腰三角形 5、同角或等角的补角(余角) 6、等角加(减)等角
7、平行线 8、等于同一角的两个角相等
缺条边的条件:
【例题讲解】
例1. 如图:AE、BC交于点M,F点在AM上,BE∥CF,BE=CF。求证:AM是△ABC的中线。
变式1. 如图,已知点从M、N分别在等边△ABC的边BC、CA上,AM、BN交于点Q,且∠BQM=60°.求证:BM=CN.
例2. 如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC。求证:(1)EC=BF;(2)EC⊥BF
变式1. 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连结AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证:(1)FC=AD; (2)AB=BC+AD.
例3. 某同学把一块三角形的玻璃打碎成了3块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的方法是( )
A、带①去; B、带②去; C、带③去; D、①②③都带去.
变式1. 如图所示,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
例4. 如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线BG于G点,DE⊥DF,交AB于点E,连结EG、EF
⑴求证:BG=CF
⑵请你判断BE+CF与EF的大小关系,并说明理由。
.
变式1. 如图,已知AE=DE,AE⊥DE,AB⊥BC,DC⊥BC,求证:AB+CD=BC。
变式2. 已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F.
(1)如图1,求证:△ACE≌△DCB.
(2)如图1,若∠ACD=60°,则∠AFB= ;如图2,若∠ACD=90°,则∠AFB= ;
(3)如图3,若∠ACD=β,则∠AFB= (用含β的式子表示)并说明理由.
随堂演练
1、如图,∠ACB=∠ADB=90°,AC=BD,AC、BD相交于O点,则(1)AD=BC; (2)∠DBC=∠CAD; (3)AO=BO; (4)AB‖CD。其中正确式子的序号有_____________。
第1题 第2题
2、在△ABC中,AB=AC,D、E两点在BC上,且有AD=AE,BD=CE,若∠BAD=30°,∠DAE=50°,则∠BAC的度数为()
A.130°? B.120°? C.110°? D.100°?
3、已知图中的两个三角形全等,则的度数是( )
A.72° B.60° C.58° D.50°
4、在与中,已有条件,还需添加两个条件才能使,不能添加的一组条件是()
A.,
B.,
C.,
D.,
12、如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,AD=AC,AF平分∠CAB交CE于点F,DF的延长线交AC于点G
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
