1.3.1二项式定理(共32张PPT)
文档属性
| 名称 | 1.3.1二项式定理(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-22 12:43:59 | ||
图片预览











文档简介
(共32张PPT)
若今天是星期一,再过810天后的那一天是星期几?
在初中,我们已经学过了
(a+b)2=a2+2ab+b2
(a+b)3=(a+b)2(a+b)=a3+3a2b+3ab2+b3
对于(a+b)4,(a+b)5 如何展开?
(a+b)100又怎么办? (a+b)n (n∈N+)呢?
我们知道,事物之间或多或少存在着规律. 这节课,我们就来研究(a+b)n的二项展开式的规律性.
规律:
(a+b)1=a+b
(a+b)2=(a+b)(a+b)=a?a+a?b+b?a+b?b=a2+2ab+b2
(a+b)3=(a+b)2(a+b)=(a2+2ab+b2)(a+b)
=a3+3a2b+ 3ab2+b3 (a+b)4=(a+b)3(a+b)=(a3+3a2b+3ab2+b3)(a+b)
=a4+4a3b+6a2b2+4ab3+b4
如何从组合知识得到(a+b)4展开式中各项的系数?
(a+b)4=(a+b)(a+b)(a+b)(a+b)
(1)若每个括号都不取b,只有一种取法得到a4;
(2)若只有一个括号取b,共有种取法得到a3b;
(3)若只有两个括号取b,共有种取法得到a2b2;
(4)若只有三个括号取b,共有种取法得到ab3;
(5)若每个括号都取b,共有种取法得b4.
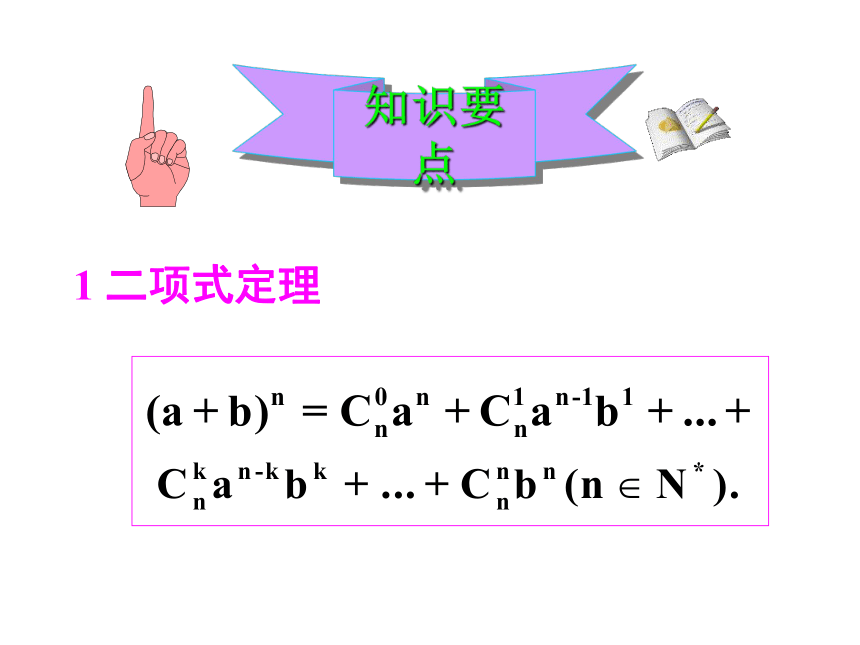
1 二项式定理
证明:
由于(a+b)n是(a+b)相乘,每个(a+b)在相乘时有两种选择,选a或b,而且每个(a+b)中的a或b都选定后,才能得到展开式的一项.
因此,由分步乘法计数原理可知,在合并同类项之前, (a+b)n的展开式共有2n项,其中每一项都是an-kbk(k=0,1,…,n)的形式.
对于某个k( ),对应的项an-kbk是由n-k个(a+b)中选a,k个(a+b)中选b得到的. 由于b选定后,a的选法也随之确定.
因此, an-kbk出现的次数相当于从n个(a+b)中取k个b的组合数 . 这样,(a+b)n的展开式中, an-kbk共有 个,将它们合并同类项,就可以得到二项展开式:
对二项式定理的理解
(1)它有n+1项;
(2)各项的次数都等于二项式的次数n;
(3)字母a按降幂排列,次数由n递减到0;字母b按升幂排列,次数由0递增到n.
2 二项式系数
我们看到的二项展开式共有n+1项,其中各项的系数 ( )叫做二项式系数(binomial coefficient).
3 通项
式中的 叫做二项展开式的通项,用 Tk+1 表示,即通项为展开式的第k+1项:
对通项的理解
(1)它是(a+b)n的展开式的第k+1项,这里k=0,1,2,…,n;
(2)字母a,b是一种“符号”,实际上它们可以是数、式及其它什么的,只要具备二项式的形式就可以用定理写出展开式;
(3)展开式是对(a+b)n这个标准形式而言的,还可以对等式进行变形.
思考(1)如何求展开式中的第三项?
(2)如何求展开式中第三项的系数?
方法(1)用定理展开,再找指定项;
(2)用通项公式.
解:
(2)先将原式化简,再展开,得
1. 的展开式中,第五项是……( )
A. B. C. D.
2. 的展开式中,不含a的项是第( )
A.7 项 B.8 项 C.9 项 D.6项
要解答上题必须熟记二项式定理
上题答案:
(1) B
(2) A
求近似值(精确到0.001)
(1)(0.997)3 (2)(1.002)6
分析:
(1)(0.997)3=(1-0.003)3
(2)(1.002)6=(1+0.002)6
类似这样的近似计算转化为二项式定理求展开式,按精确度展开到一定项.
分析:方法一用通项公式(适用于任意次幂)
方法二用定理展开(次数较小时使用)
答案:
1.二项式定理
二项式定理(a+b)n=Cn0an+Cn1an-1b+…+
Cnran-rbr+…+Cnnbn是通过不完全归纳法,并结合组合的概念得到展开式的规律性,然后用数学归纳法加以证明.
2.二项式定理的特点
(1)项数:共n+1项,是关于a与b的齐次多项式
(2)系数
(3)指数 :a的指数从n逐项递减到0,是降幂排 列;b的指数从0逐项递增到n,是升幂排列.
1. (2018年安徽、河北卷)在 的展开式中,常数项是______.
A.14 B.-14 C.42 D. -42
解析:
则k=6,故展开式中的常数项是
,选答案A.
令
2.(2018年全国)在(x-a)10的展开式中,x7的系数是15,则实数a的值为_______.
-1/2
解析:
1.填空
(1)(x+2)10(x2-1)的展开式中x10的系数为_____.
(2)在(x-1)11的展开式中,x的偶次幂的所有项的系数的和为______ .
1.179
-210
2.选择
(1)( i)12展开式中所有奇数项的和是( )
A.-1 B.1 C.0 D.i
(2) 数11100-1的末尾连续的零的个数是( )
A.0 B.3 C.5 D.7
√
√
)r=C12r
3.解答题
(1)求( + )12展开式中所有的有理数项.
解:
通项为Tr+1=C12r(
)12-r(
(r=0,1,2,…,12),为得有理数项,只需r是6的倍数,即r=0,6,12,即有理数项为T1=C120·24=16,T7=C126·22·33=99792,T13=C1212·36=729.
(2)二项式 的展开式中第三项系数比第二项系数大44,求第4项的系数.
分析:由第三项系数比第二项系数大44先求n, 再由通项求第四项系数.
答案:165
(3) 某班有男、女学生各n人,现在按照男生至少一人,女生至多n人选法,将选出的学生编成社会实践小组,试证明:这样的小组的选法共有2n(2n-1)种.
证:依题意,这些小组中女生人数分别是Cn0,Cn1,Cn2,…,Cnn个.对于上述女生人数的每种情况,男生人数可以有Cn0,Cn1,Cn2,…,Cnn个。
根据乘法原理和加法原理可得
Cn0Cn1+Cn0Cn2+…+Cn0Cnn+Cn1Cn1+…+Cn1Cn2+Cn2Cn1+Cn2Cn2+…+Cn2Cnn+…CnnCn1+ Cnn Cn2+…+ Cnn Cnn
= Cn0(Cn1+Cn2+…+ Cnn)+Cn1 (Cn1+Cn2+…+ Cnn)+Cn2(Cn1+Cn2+…+Cnn)+…+Cnn(Cn1+Cn2+…+ Cnn)
=(Cn1+Cn2+…+ Cnn)(Cn0 +Cn1+Cn2+…+ Cnn)
=(2n-1)2n
∴ 依题意所编成的小组共有2n(2n-1)个.
若今天是星期一,再过810天后的那一天是星期几?
在初中,我们已经学过了
(a+b)2=a2+2ab+b2
(a+b)3=(a+b)2(a+b)=a3+3a2b+3ab2+b3
对于(a+b)4,(a+b)5 如何展开?
(a+b)100又怎么办? (a+b)n (n∈N+)呢?
我们知道,事物之间或多或少存在着规律. 这节课,我们就来研究(a+b)n的二项展开式的规律性.
规律:
(a+b)1=a+b
(a+b)2=(a+b)(a+b)=a?a+a?b+b?a+b?b=a2+2ab+b2
(a+b)3=(a+b)2(a+b)=(a2+2ab+b2)(a+b)
=a3+3a2b+ 3ab2+b3 (a+b)4=(a+b)3(a+b)=(a3+3a2b+3ab2+b3)(a+b)
=a4+4a3b+6a2b2+4ab3+b4
如何从组合知识得到(a+b)4展开式中各项的系数?
(a+b)4=(a+b)(a+b)(a+b)(a+b)
(1)若每个括号都不取b,只有一种取法得到a4;
(2)若只有一个括号取b,共有种取法得到a3b;
(3)若只有两个括号取b,共有种取法得到a2b2;
(4)若只有三个括号取b,共有种取法得到ab3;
(5)若每个括号都取b,共有种取法得b4.
1 二项式定理
证明:
由于(a+b)n是(a+b)相乘,每个(a+b)在相乘时有两种选择,选a或b,而且每个(a+b)中的a或b都选定后,才能得到展开式的一项.
因此,由分步乘法计数原理可知,在合并同类项之前, (a+b)n的展开式共有2n项,其中每一项都是an-kbk(k=0,1,…,n)的形式.
对于某个k( ),对应的项an-kbk是由n-k个(a+b)中选a,k个(a+b)中选b得到的. 由于b选定后,a的选法也随之确定.
因此, an-kbk出现的次数相当于从n个(a+b)中取k个b的组合数 . 这样,(a+b)n的展开式中, an-kbk共有 个,将它们合并同类项,就可以得到二项展开式:
对二项式定理的理解
(1)它有n+1项;
(2)各项的次数都等于二项式的次数n;
(3)字母a按降幂排列,次数由n递减到0;字母b按升幂排列,次数由0递增到n.
2 二项式系数
我们看到的二项展开式共有n+1项,其中各项的系数 ( )叫做二项式系数(binomial coefficient).
3 通项
式中的 叫做二项展开式的通项,用 Tk+1 表示,即通项为展开式的第k+1项:
对通项的理解
(1)它是(a+b)n的展开式的第k+1项,这里k=0,1,2,…,n;
(2)字母a,b是一种“符号”,实际上它们可以是数、式及其它什么的,只要具备二项式的形式就可以用定理写出展开式;
(3)展开式是对(a+b)n这个标准形式而言的,还可以对等式进行变形.
思考(1)如何求展开式中的第三项?
(2)如何求展开式中第三项的系数?
方法(1)用定理展开,再找指定项;
(2)用通项公式.
解:
(2)先将原式化简,再展开,得
1. 的展开式中,第五项是……( )
A. B. C. D.
2. 的展开式中,不含a的项是第( )
A.7 项 B.8 项 C.9 项 D.6项
要解答上题必须熟记二项式定理
上题答案:
(1) B
(2) A
求近似值(精确到0.001)
(1)(0.997)3 (2)(1.002)6
分析:
(1)(0.997)3=(1-0.003)3
(2)(1.002)6=(1+0.002)6
类似这样的近似计算转化为二项式定理求展开式,按精确度展开到一定项.
分析:方法一用通项公式(适用于任意次幂)
方法二用定理展开(次数较小时使用)
答案:
1.二项式定理
二项式定理(a+b)n=Cn0an+Cn1an-1b+…+
Cnran-rbr+…+Cnnbn是通过不完全归纳法,并结合组合的概念得到展开式的规律性,然后用数学归纳法加以证明.
2.二项式定理的特点
(1)项数:共n+1项,是关于a与b的齐次多项式
(2)系数
(3)指数 :a的指数从n逐项递减到0,是降幂排 列;b的指数从0逐项递增到n,是升幂排列.
1. (2018年安徽、河北卷)在 的展开式中,常数项是______.
A.14 B.-14 C.42 D. -42
解析:
则k=6,故展开式中的常数项是
,选答案A.
令
2.(2018年全国)在(x-a)10的展开式中,x7的系数是15,则实数a的值为_______.
-1/2
解析:
1.填空
(1)(x+2)10(x2-1)的展开式中x10的系数为_____.
(2)在(x-1)11的展开式中,x的偶次幂的所有项的系数的和为______ .
1.179
-210
2.选择
(1)( i)12展开式中所有奇数项的和是( )
A.-1 B.1 C.0 D.i
(2) 数11100-1的末尾连续的零的个数是( )
A.0 B.3 C.5 D.7
√
√
)r=C12r
3.解答题
(1)求( + )12展开式中所有的有理数项.
解:
通项为Tr+1=C12r(
)12-r(
(r=0,1,2,…,12),为得有理数项,只需r是6的倍数,即r=0,6,12,即有理数项为T1=C120·24=16,T7=C126·22·33=99792,T13=C1212·36=729.
(2)二项式 的展开式中第三项系数比第二项系数大44,求第4项的系数.
分析:由第三项系数比第二项系数大44先求n, 再由通项求第四项系数.
答案:165
(3) 某班有男、女学生各n人,现在按照男生至少一人,女生至多n人选法,将选出的学生编成社会实践小组,试证明:这样的小组的选法共有2n(2n-1)种.
证:依题意,这些小组中女生人数分别是Cn0,Cn1,Cn2,…,Cnn个.对于上述女生人数的每种情况,男生人数可以有Cn0,Cn1,Cn2,…,Cnn个。
根据乘法原理和加法原理可得
Cn0Cn1+Cn0Cn2+…+Cn0Cnn+Cn1Cn1+…+Cn1Cn2+Cn2Cn1+Cn2Cn2+…+Cn2Cnn+…CnnCn1+ Cnn Cn2+…+ Cnn Cnn
= Cn0(Cn1+Cn2+…+ Cnn)+Cn1 (Cn1+Cn2+…+ Cnn)+Cn2(Cn1+Cn2+…+Cnn)+…+Cnn(Cn1+Cn2+…+ Cnn)
=(Cn1+Cn2+…+ Cnn)(Cn0 +Cn1+Cn2+…+ Cnn)
=(2n-1)2n
∴ 依题意所编成的小组共有2n(2n-1)个.
