1.3.2“杨辉三角”与二项式系数的性质(共33张PPT)
文档属性
| 名称 | 1.3.2“杨辉三角”与二项式系数的性质(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-22 00:00:00 | ||
图片预览








文档简介
(共33张PPT)
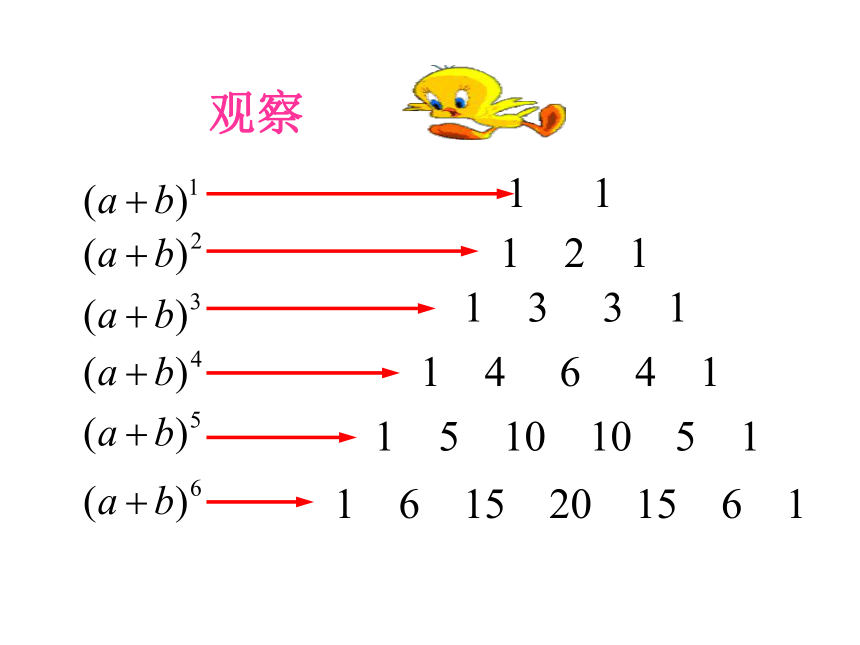
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
(1)上述的表叫做二项式系数的表,观察表中二项式系数的规律,并加以归纳.
(2)继续观察,归纳每行二项式系数的特点(即二项式系数的性质),猜测出二项式系数的性质.
南宋末年钱塘人,是当时有名的数学家和教育家,杨辉一生编写的数学书很多,但散佚严重.
杨辉生活在浙江杭州一带,曾当过地方官,到过苏州、台州等地,他每到一处都会有人慕名前来 请教数学问题.
杨辉
本节课的课题《二项式定理》就是研究 (a+b)的平方,(a+b)的三次方…… (a+b)的n次方的乘法展开式的规律, 法国数学家帕斯卡在17世纪发现了它,国外把这一规律称为帕斯卡三角.其实,我国数学家杨辉早在1261年在他的《详解九章算法》中就有了相应的图表.
《九章算术》
《详解九章算法》中记载的表
展开式的二项式系数依次是:
从函数角度看, 可看成是以r为自变量的函数 ,其定义域是:
当 时,其图象是右图中的7个孤立点.
由以上分析可以画出如下图:
结合杨辉三角和上图来研究二项式系数的一些性质.
1.对称性
与首末两端“等距离”的两个二项式系数相等.
这一性质可直接由公式Cnm=Cnn-m 得到.
直线 将函数 的图像分成对称的两部分,它是图像的对称轴
2.增减性与最大值
由于:
所以 相对于 的增减情况由 决定.
由:
二项式系数是逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值.
可知,当 时,
当n为奇数时,中间两项的二项式系数 、
相等,且同时取得最大值.
3.各二项式系数之和
已知 (1+x)n=Cn0+Cn1x+…+Cnrxr+…+Cnnxn
令x=1,则
2n=Cn0+Cn1+…+Cnn
证明在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和
分析:
奇数项的二项式系数的和为Cn0+Cn2+…
偶数项的二项式系数的和为Cn1+Cn3+…
由于在二项式定理中a、b可以取任意实数,因此我们可以通过对a、b适当赋值来得到上述两个系数和.
证明:
在二项展开式中,令a=1,b=-1,则得
(1-1)n=Cn0-Cn1+Cn2-Cn3+…+(-1)nCnn
即
0=(Cn0+Cn2 +…)-(Cn1+Cn3+…),
所以
Cn0+Cn2 +…= Cn1+Cn3+…,
即得证.
1.二项式系数的三条性质
(1)对称性;
(2)增减性与最大值;
(3)各二项式系数的和;
(4)递推性(杨辉三角中).
2. 数学思想方法
(1)函数法;
(2)特殊值法 ;
(3)赋值法 、递推法、图象法.
3.“系数”与“二项式系数”的区别
不能混淆两者,只有二项式系数最大的才是中间项,而系数最大的不一定是中间项.
1. (2018年上海春季高考卷)如图1,在由二项式系数所构成的杨辉三角中,第______行中从左到右第14与第15个数的比为2:3 .
34
解析:
由图1我们能发现,第1行中的数是
第2行中的数是
第3行中的数是
则第n行中的数是
设第n行中从左到右第14与第15个数的比为
则
,解得
2.(2019年湖北)(1-x3)?(1+x)10的展开式中含x4的项的系数为_____(用数字作答).
解析:
∵(1-x3)(1+x)10
=(1-x3)(1+C101x+C102x2+C103x3+C104x4+…),
∴x4的系数为C104+(-1) C101=200.
200
(1)Cn1+Cn2+…+Cnn=_____;
C111+C113+C115+C117+C119+C1111=_____.
(2)在(1+x)10的展开式中,二项式系数最大为 __;
在(1-x)11的展开式中,二项式系数最大为____ .
1.填空
(1) 的展开式中,无理项的个 数是( )
A .83 B.84 C.85 D.86
(2)(x-2)9的展开式中,第6项的二项式系数 是( )
A.4032 B.-4032 C.126 D.-126
2.选择
√
√
3.解答题
(1)求(2x+3y)6的展开式的第三项.
解:
由二项展开式的通项知
T3=T2+1=C62(2x)6-2(3y)2=2160x4y2
(2)求(2a+3b)6的展开式的第三项的二项式系数.
解:
由二项展开式的通项知
T3=T2+1=C62(2a)6-2(3b)2=2160a4b2
由二项式系数定义知,展开式的第三项的二项式系数为C62=15,而展开式的第三项的系数为2160.
1.
(1)当n是偶数时,最大值 ;当n是奇数时,最大值是 .
(2)C111+C113+…+C1111=*211=1024.
(3)
2.
∵2n=Cn0+Cn1+…+Cnn
Cn0+Cn2 +…= Cn1+Cn3+…,
∴ Cn0+Cn2 +…= 2n-1
3.略.
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
(1)上述的表叫做二项式系数的表,观察表中二项式系数的规律,并加以归纳.
(2)继续观察,归纳每行二项式系数的特点(即二项式系数的性质),猜测出二项式系数的性质.
南宋末年钱塘人,是当时有名的数学家和教育家,杨辉一生编写的数学书很多,但散佚严重.
杨辉生活在浙江杭州一带,曾当过地方官,到过苏州、台州等地,他每到一处都会有人慕名前来 请教数学问题.
杨辉
本节课的课题《二项式定理》就是研究 (a+b)的平方,(a+b)的三次方…… (a+b)的n次方的乘法展开式的规律, 法国数学家帕斯卡在17世纪发现了它,国外把这一规律称为帕斯卡三角.其实,我国数学家杨辉早在1261年在他的《详解九章算法》中就有了相应的图表.
《九章算术》
《详解九章算法》中记载的表
展开式的二项式系数依次是:
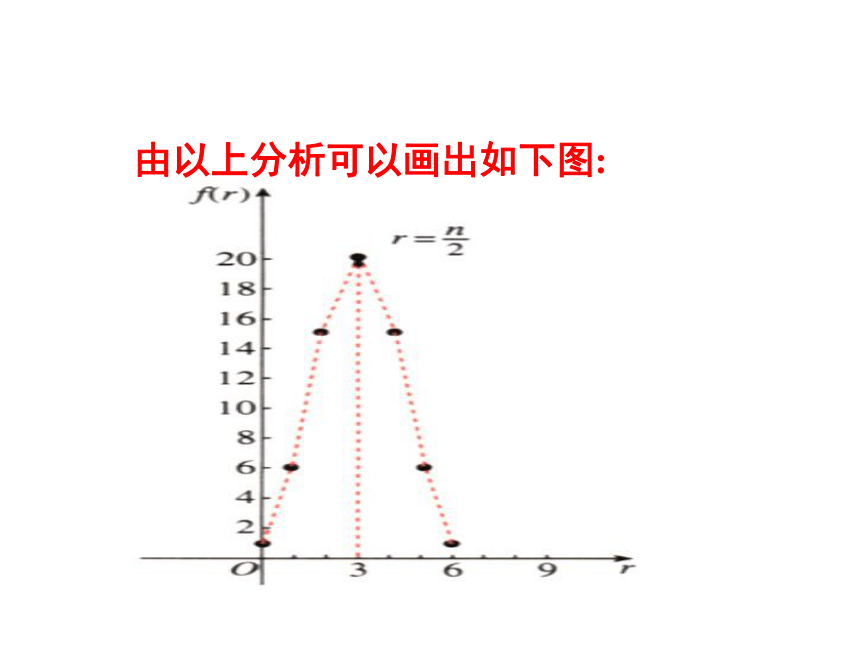
从函数角度看, 可看成是以r为自变量的函数 ,其定义域是:
当 时,其图象是右图中的7个孤立点.
由以上分析可以画出如下图:
结合杨辉三角和上图来研究二项式系数的一些性质.
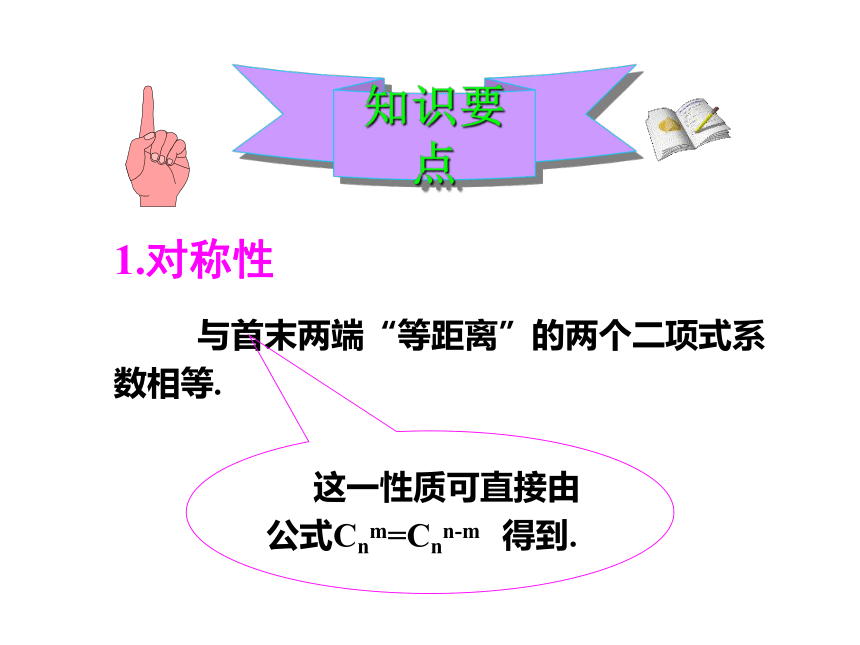
1.对称性
与首末两端“等距离”的两个二项式系数相等.
这一性质可直接由公式Cnm=Cnn-m 得到.
直线 将函数 的图像分成对称的两部分,它是图像的对称轴
2.增减性与最大值
由于:
所以 相对于 的增减情况由 决定.
由:
二项式系数是逐渐增大的,由对称性可知它的后半部分是逐渐减小的,且中间项取得最大值.
可知,当 时,
当n为奇数时,中间两项的二项式系数 、
相等,且同时取得最大值.
3.各二项式系数之和
已知 (1+x)n=Cn0+Cn1x+…+Cnrxr+…+Cnnxn
令x=1,则
2n=Cn0+Cn1+…+Cnn
证明在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和
分析:
奇数项的二项式系数的和为Cn0+Cn2+…
偶数项的二项式系数的和为Cn1+Cn3+…
由于在二项式定理中a、b可以取任意实数,因此我们可以通过对a、b适当赋值来得到上述两个系数和.
证明:
在二项展开式中,令a=1,b=-1,则得
(1-1)n=Cn0-Cn1+Cn2-Cn3+…+(-1)nCnn
即
0=(Cn0+Cn2 +…)-(Cn1+Cn3+…),
所以
Cn0+Cn2 +…= Cn1+Cn3+…,
即得证.
1.二项式系数的三条性质
(1)对称性;
(2)增减性与最大值;
(3)各二项式系数的和;
(4)递推性(杨辉三角中).
2. 数学思想方法
(1)函数法;
(2)特殊值法 ;
(3)赋值法 、递推法、图象法.
3.“系数”与“二项式系数”的区别
不能混淆两者,只有二项式系数最大的才是中间项,而系数最大的不一定是中间项.
1. (2018年上海春季高考卷)如图1,在由二项式系数所构成的杨辉三角中,第______行中从左到右第14与第15个数的比为2:3 .
34
解析:
由图1我们能发现,第1行中的数是
第2行中的数是
第3行中的数是
则第n行中的数是
设第n行中从左到右第14与第15个数的比为
则
,解得
2.(2019年湖北)(1-x3)?(1+x)10的展开式中含x4的项的系数为_____(用数字作答).
解析:
∵(1-x3)(1+x)10
=(1-x3)(1+C101x+C102x2+C103x3+C104x4+…),
∴x4的系数为C104+(-1) C101=200.
200
(1)Cn1+Cn2+…+Cnn=_____;
C111+C113+C115+C117+C119+C1111=_____.
(2)在(1+x)10的展开式中,二项式系数最大为 __;
在(1-x)11的展开式中,二项式系数最大为____ .
1.填空
(1) 的展开式中,无理项的个 数是( )
A .83 B.84 C.85 D.86
(2)(x-2)9的展开式中,第6项的二项式系数 是( )
A.4032 B.-4032 C.126 D.-126
2.选择
√
√
3.解答题
(1)求(2x+3y)6的展开式的第三项.
解:
由二项展开式的通项知
T3=T2+1=C62(2x)6-2(3y)2=2160x4y2
(2)求(2a+3b)6的展开式的第三项的二项式系数.
解:
由二项展开式的通项知
T3=T2+1=C62(2a)6-2(3b)2=2160a4b2
由二项式系数定义知,展开式的第三项的二项式系数为C62=15,而展开式的第三项的系数为2160.
1.
(1)当n是偶数时,最大值 ;当n是奇数时,最大值是 .
(2)C111+C113+…+C1111=*211=1024.
(3)
2.
∵2n=Cn0+Cn1+…+Cnn
Cn0+Cn2 +…= Cn1+Cn3+…,
∴ Cn0+Cn2 +…= 2n-1
3.略.
