1.2.1排列(共31张PPT)
图片预览











文档简介
(共31张PPT)
由数字1,2,3,4可以组成多少个没有重复数字的三位数?
假如由数字1~9这几个数字可以组成多少个没有重复数字的三位数?
上节课,我们一起学习了两个基本原理及基本原理的简单应用,这一节,我们将继续应用基本原理研究排列问题.
某学校计划在元旦安排一场师生联欢会,需要从甲、乙、丙三名候选人选2名作主持人,其中1名作正式主持人,一名作候补主持人,有多少种不同的方法?
解决上述问题,可以应用分步计数原理进行,可分两步:第1步,确定正式主持人,从3人中任选1人,有3种不同选法;第2步,确定候补主持人,从余下的2人中选取,有2种不同的方法.
根据分步计数原理,在3名同学中选2名,按照参加正式主持人在前,候补主持人在后的不同顺序排列方法有3×2=6种.
我们把上面问题中被取的对象叫做元素.于是,所提出问题就是从3个不同的元素a、b、c中任取2个,然后按一定的顺序排成一列,求一共有多少种不同的排列方法.所有不同排列为ab,ac,ba,bc,ca,cb,所有排列的种数为3×2=6.
如果我们把上述问题再推广到更为一般的情形,就得到排列及排列数的概念.
1 排列
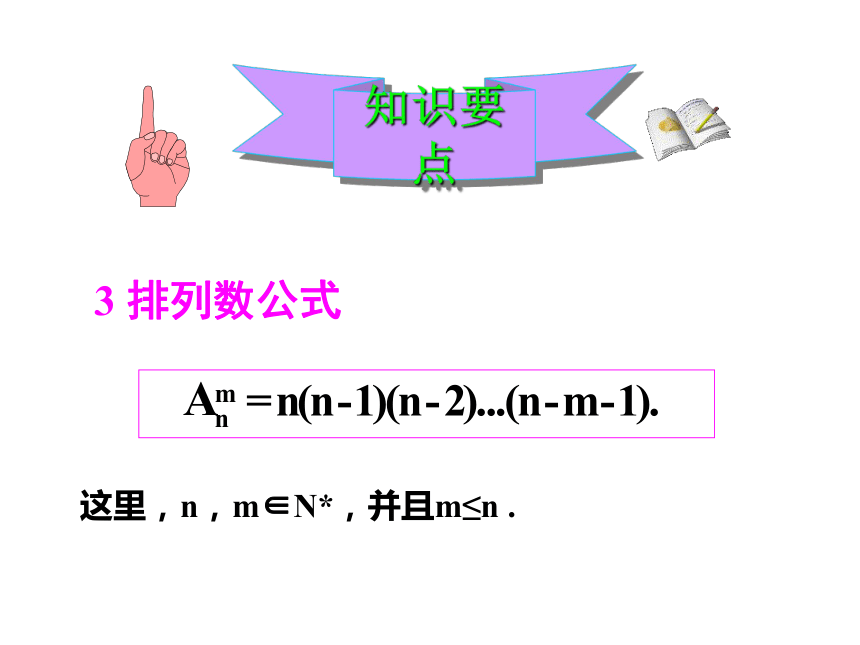
一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素取出m个元素的排列.
根据排列的定义,两个排列相同,当且仅当两个排列的元素完全相同,且元素的排列顺序也相同.
4 全排列
n个不同元素全部取出的一个排列,叫做n个不同元素的一个全排列.这是公式中m=n,即有
也就是说,n个元素全部取出的排列数,等于1到n的连乘积.即n的阶乘,用n!表示.
6!=6×5×4×3×2×1=720
求下列各式中n值:
解析:该题是对排列数公式的考察
某段铁路上有12个车站,共需要准备多少种普通客票?
解:
用 0 到 9 这十个数字,可以组成多少个没有重复数字的三位数?
解法一:对排列方法分步思考.
解法二:对排列方法分类思考.
符合条件的三位数可分为两类:
根据加法原理
解法三:间接法.
从0到9这十个数字中任取三个数字的排列数为 ,
∴ 所求的三位数的个数是
1. 知识要求:
(1)要求大家在理解排列的意义的基础上,掌握排列数的运算;
(2)了解科学计算器的阶乘运算功能,为进一步学习排列的应用打好基础.
2.重点掌握排列的两个公式:
1 (2019年海南)用1,2,3,4,5这五个数字,组成没有重复数字的三位数,其中偶数共有______个.
A 24 B 30 C 40 D 60
A
先分类,再分步
2.(2019年湖北卷理)将甲、乙、丙、丁四名学生分到三个不同的班,每个班至少分到一名学生,且甲、乙两名学生不能分到同一个班,则不同分法的种数为 ______.
A 18 B 24 C 30 D 36
C
解析:
用间接法解答:四名学生中有两名学生分在一个班的种数是 ,顺序有 种,而甲乙被分在同一个班的有 种,所以种数是
1.填空
(1)从7盆不同的盆花中选出5盆摆放在主席台前,其中有两盆花不宜摆放在正中间,则一共有_____种不同的摆放方法(用数字作答).
(2) 5人成一排,要求甲、已相邻,有_____种排法.
1800
48
2.选择
(1)将5列车停在5条不同的轨道上,其中a列车不停在第一轨道上,b列车不停在第二轨道上,那么不同的停放方法有( ).
A 120种 B 96种 C 78种 D 72种
(2)七人排成一排,甲、乙两人必须相邻,且甲、乙都不与丙相邻,则不同的排法( )种.
A 960种 B 840种 C 720种 D 600种
√
√
3.解答题
(1)有棋盘型街道如图,某人由 A 点到 B 点取捷径
① 共有几种走法?
②若不过 D 点,取捷径的走法共有几种?
解:
(2)用0、1、2、3、4、5六个数字,若数字可以重复,则可以构成几个三位数?其中奇数共几个?
解:
由于0不能排在百位,所以百位有5种方法,而十位与个位皆有6种方法,故共可排成 5 × 6 × 6 = 180 个三位数.
若所排成的三位数为奇數,则个位可以排1、3、5共3种方法,而百位有5种,十位有6种排法,故共可排成 5 × 6 × 3 = 90 个奇数.
(3) 计划展出不同的画10幅,其中一幅水彩画、4幅油画、5幅国画,排成一行陈列,要求同一品种的画必须连在一起,并且水彩画不能放在两端,那么不同的陈列方式有多少种?
解:
由数字1,2,3,4可以组成多少个没有重复数字的三位数?
假如由数字1~9这几个数字可以组成多少个没有重复数字的三位数?
上节课,我们一起学习了两个基本原理及基本原理的简单应用,这一节,我们将继续应用基本原理研究排列问题.
某学校计划在元旦安排一场师生联欢会,需要从甲、乙、丙三名候选人选2名作主持人,其中1名作正式主持人,一名作候补主持人,有多少种不同的方法?
解决上述问题,可以应用分步计数原理进行,可分两步:第1步,确定正式主持人,从3人中任选1人,有3种不同选法;第2步,确定候补主持人,从余下的2人中选取,有2种不同的方法.
根据分步计数原理,在3名同学中选2名,按照参加正式主持人在前,候补主持人在后的不同顺序排列方法有3×2=6种.
我们把上面问题中被取的对象叫做元素.于是,所提出问题就是从3个不同的元素a、b、c中任取2个,然后按一定的顺序排成一列,求一共有多少种不同的排列方法.所有不同排列为ab,ac,ba,bc,ca,cb,所有排列的种数为3×2=6.
如果我们把上述问题再推广到更为一般的情形,就得到排列及排列数的概念.
1 排列
一般地,从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列,叫做从n个不同元素取出m个元素的排列.
根据排列的定义,两个排列相同,当且仅当两个排列的元素完全相同,且元素的排列顺序也相同.
4 全排列
n个不同元素全部取出的一个排列,叫做n个不同元素的一个全排列.这是公式中m=n,即有
也就是说,n个元素全部取出的排列数,等于1到n的连乘积.即n的阶乘,用n!表示.
6!=6×5×4×3×2×1=720
求下列各式中n值:
解析:该题是对排列数公式的考察
某段铁路上有12个车站,共需要准备多少种普通客票?
解:
用 0 到 9 这十个数字,可以组成多少个没有重复数字的三位数?
解法一:对排列方法分步思考.
解法二:对排列方法分类思考.
符合条件的三位数可分为两类:
根据加法原理
解法三:间接法.
从0到9这十个数字中任取三个数字的排列数为 ,
∴ 所求的三位数的个数是
1. 知识要求:
(1)要求大家在理解排列的意义的基础上,掌握排列数的运算;
(2)了解科学计算器的阶乘运算功能,为进一步学习排列的应用打好基础.
2.重点掌握排列的两个公式:
1 (2019年海南)用1,2,3,4,5这五个数字,组成没有重复数字的三位数,其中偶数共有______个.
A 24 B 30 C 40 D 60
A
先分类,再分步
2.(2019年湖北卷理)将甲、乙、丙、丁四名学生分到三个不同的班,每个班至少分到一名学生,且甲、乙两名学生不能分到同一个班,则不同分法的种数为 ______.
A 18 B 24 C 30 D 36
C
解析:
用间接法解答:四名学生中有两名学生分在一个班的种数是 ,顺序有 种,而甲乙被分在同一个班的有 种,所以种数是
1.填空
(1)从7盆不同的盆花中选出5盆摆放在主席台前,其中有两盆花不宜摆放在正中间,则一共有_____种不同的摆放方法(用数字作答).
(2) 5人成一排,要求甲、已相邻,有_____种排法.
1800
48
2.选择
(1)将5列车停在5条不同的轨道上,其中a列车不停在第一轨道上,b列车不停在第二轨道上,那么不同的停放方法有( ).
A 120种 B 96种 C 78种 D 72种
(2)七人排成一排,甲、乙两人必须相邻,且甲、乙都不与丙相邻,则不同的排法( )种.
A 960种 B 840种 C 720种 D 600种
√
√
3.解答题
(1)有棋盘型街道如图,某人由 A 点到 B 点取捷径
① 共有几种走法?
②若不过 D 点,取捷径的走法共有几种?
解:
(2)用0、1、2、3、4、5六个数字,若数字可以重复,则可以构成几个三位数?其中奇数共几个?
解:
由于0不能排在百位,所以百位有5种方法,而十位与个位皆有6种方法,故共可排成 5 × 6 × 6 = 180 个三位数.
若所排成的三位数为奇數,则个位可以排1、3、5共3种方法,而百位有5种,十位有6种排法,故共可排成 5 × 6 × 3 = 90 个奇数.
(3) 计划展出不同的画10幅,其中一幅水彩画、4幅油画、5幅国画,排成一行陈列,要求同一品种的画必须连在一起,并且水彩画不能放在两端,那么不同的陈列方式有多少种?
解:
