【人教版七年级数学下册同步精选】5.3.1 平行线的性质同步精选练习题(含解析)
文档属性
| 名称 | 【人教版七年级数学下册同步精选】5.3.1 平行线的性质同步精选练习题(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 715.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-20 21:16:54 | ||
图片预览


文档简介
5.3.1平行线的性质同步精选练习题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在ΔABC中,D、 E、F分别在AB、BC、AC上,且EF∥AB,要使DF∥BC,只需再有下列条件中的( )即可.
A.∠1=∠2 B.∠1=∠DFE C.∠1=∠AFD D.∠2=∠AFD
2.如图,已知,为角平分线,下列说法错误的是( )
A. B. C. D.
3.如图,已知∥,且∠1=120°,则∠2=( )
A.40° B.50° C.60° D.70°
4.将等腰直角三角形纸片和矩形纸片按如图方式折叠放在一起,若,则的度数为( )
A. B. C. D.
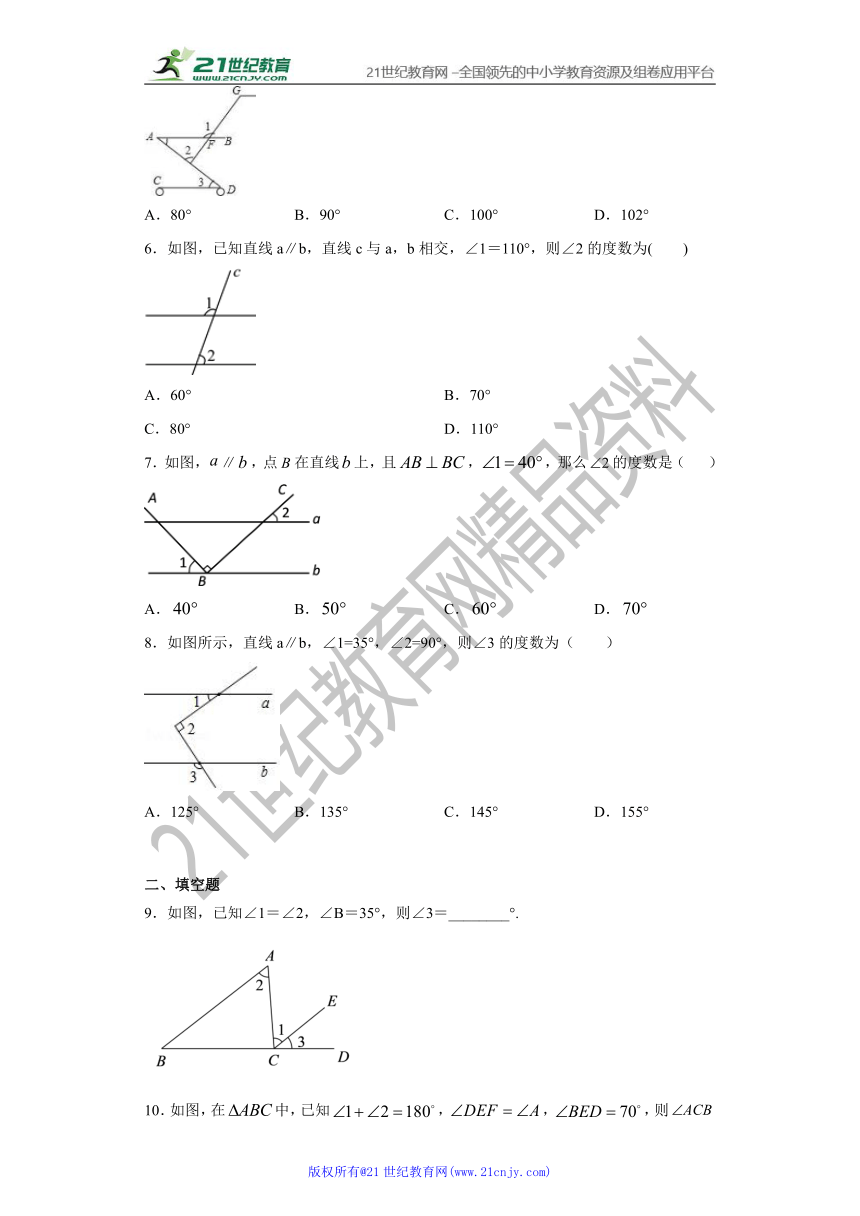
5.如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为( )
A.80° B.90° C.100° D.102°
6.如图,已知直线a∥b,直线c与a,b相交,∠1=110°,则∠2的度数为( )
A.60° B.70°
C.80° D.110°
7.如图,∥,点在直线上,且,,那么的度数是( )
A. B. C. D.
8.如图所示,直线a∥b,∠1=35°,∠2=90°,则∠3的度数为( )
A.125° B.135° C.145° D.155°
二、填空题
9.如图,已知∠1=∠2,∠B=35°,则∠3=________°.
10.如图,在中,已知,,,则的度数为__________.
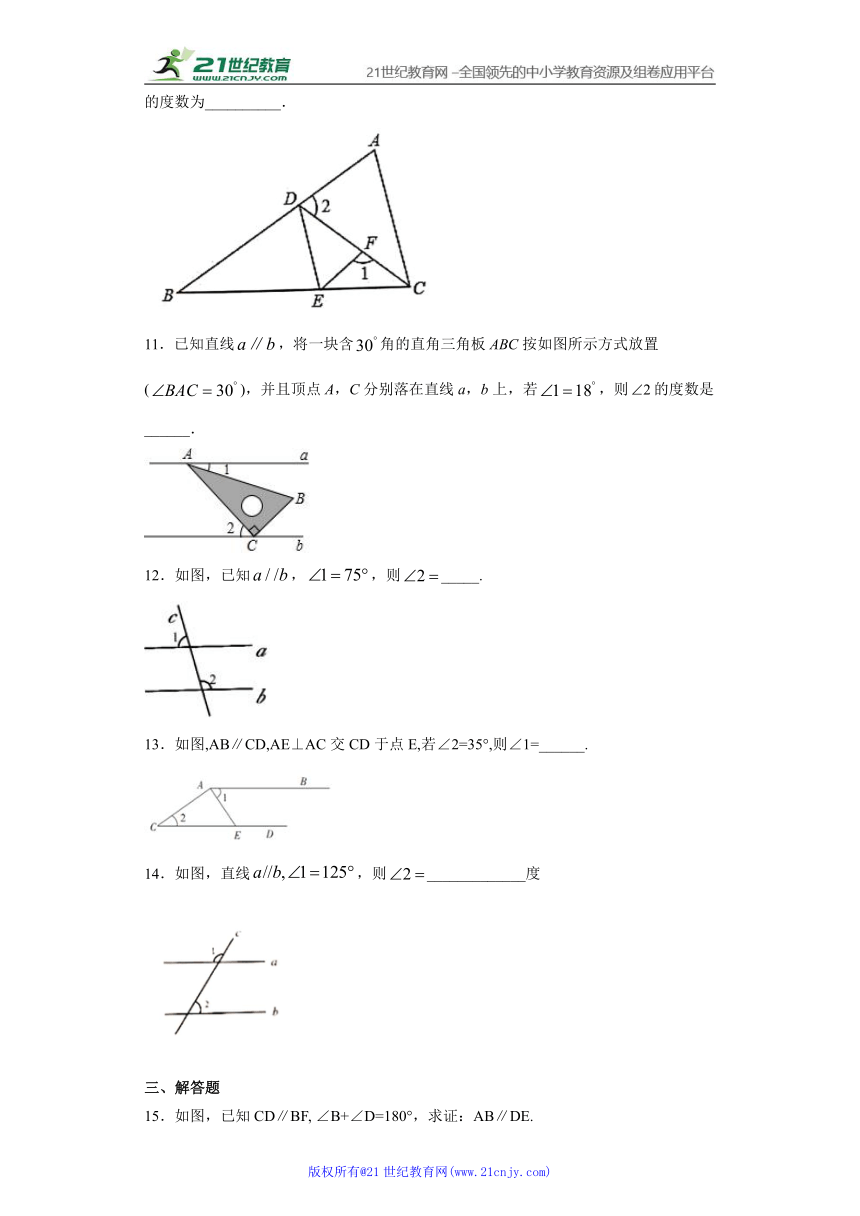
11.已知直线,将一块含角的直角三角板ABC按如图所示方式放置(),并且顶点A,C分别落在直线a,b上,若,则的度数是______.
12.如图,已知,,则_____.
13.如图,AB∥CD,AE⊥AC交CD于点E,若∠2=35°,则∠1=______.
14.如图,直线,则_____________度
三、解答题
15.如图,已知CD∥BF, ∠B+∠D=180°,求证:AB∥DE.
16.如图,D、E、F分别在△ABC的三条边上,DE∥AB,∠1+∠2=180°.
(1)试说明:DF∥AC;
(2)若∠1=110°,DF平分∠BDE,求∠C的度数.
17.完成下面的证明过程:
如图,AB∥CD,AD∥BC,BE平分∠ABC,DF平分∠ADC.
求证:BE∥DF.
证明:∵AB∥CD,(已知)
∴∠ABC+∠C=180°.( )
又∵AD∥BC,(已知)
∴ +∠C=180°.( )
∴∠ABC=∠ADC.( )
∵BE平分∠ABC,(已知)
∴∠1=∠ABC.( )
同理,∠2=∠ADC.
∴ =∠2.
∵AD∥BC,(已知)
∴∠2=∠3.( )
∴∠1=∠3,
∴BE∥DF.( )
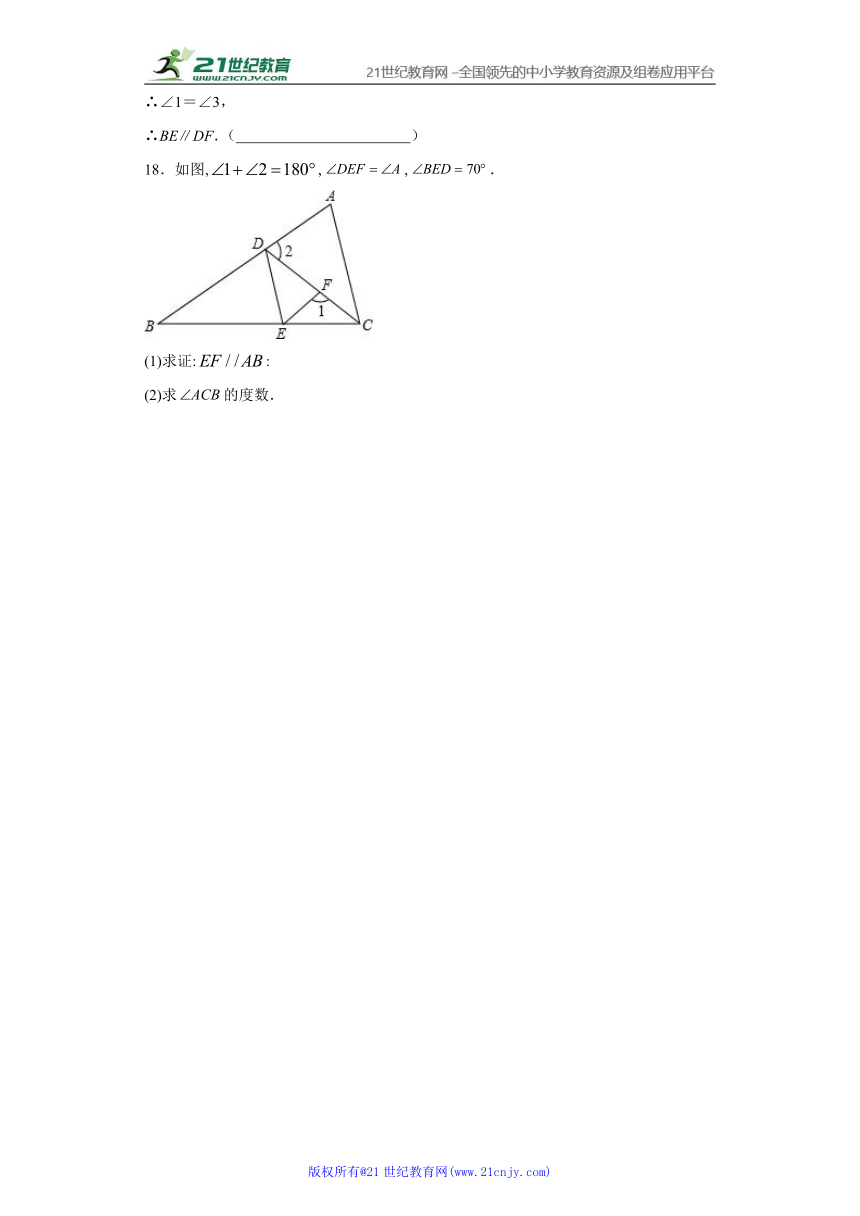
18.如图,,,.
(1)求证::
(2)求的度数.
参考答案
1.B
【解析】
∵EF∥AB,∴∠1=∠2(两直线平行,同位角相等).∵∠1=∠DFE,
∴∠2=∠DFE(等量代换),∴DF∥BC(内错角相等,两直线平行).
所以只需满足下列条件中的∠1=∠DFE.故选B.
2.B
【解析】
【分析】
利用平行线的性质得到∠2=∠4,∠3=∠2,∠5=∠1+∠2,再根据角平分线的定义得到∠1=∠2=∠4=∠3,∠5=2∠1,从而可对各选项进行判断.
【详解】
∵l1∥AB,
∴∠2=∠4,∠3=∠2,∠5=∠1+∠2,
∵AC为角平分线,
∴∠1=∠2=∠4=∠3,∠5=2∠1.
故选B.
【点睛】
本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.
3.C
【解析】
【分析】
先利用平行线的性质求出∠3的度数,再利用邻补角的定义即可求出答案.
【详解】
∵l1∥l2,
∴∠3=∠1=120°,
∴∠2=180°-∠3=60°,
故选C.
【点睛】
本题考查了平行线的性质及邻补角的定义.通过添加∠3形成同位角是解题的关键.
4.B
【解析】
【分析】
根据平行的性质即可求解.
【详解】
根据平行线的性质得到∠3=∠1=30°,
∴∠2=45°-∠3=15°.
以及等腰直角三角形的性质,故选B
【点睛】
此题主要考查平行线的性质,解题的关键是熟知两直线平行,内错角相等.
5.A
【解析】
分析:根据平行线性质求出∠A,根据三角形内角和定理得出∠2=180°∠1?∠A,代入求出即可.
详解:∵AB∥CD.
∴∠A=∠3=40°,
∵∠1=60°,
∴∠2=180°∠1?∠A=80°,
故选:A.
点睛:本题考查了平行线的性质:两直线平行,内错角相等.三角形内角和定理:三角形内角和为180°.
6.B
【解析】
【分析】
直接根据平行线的性质即可得出结论.
【详解】
∵直线a∥b,
∴∠3=∠1=110°,
∴∠2=180°?110°=70°,
故答案选B.
【点睛】
本题考查的知识点是平行线的性质,解题的关键是熟练的掌握平行线的性质.
7.B
【解析】
【分析】
由题意,求出∠3的度数,然后由∥,即可得到∠2的度数.
【详解】
解:如图:
∵,
∴∠ABC=90°,
∵,
∴,
∵∥,
∴;
故选:B.
【点睛】
本题考查了平行线的性质和角的运算,解题的关键是正确求出∠3的度数.
8.A
【解析】
分析:如图求出∠5即可解决问题.
详解:
∵a∥b,
∴∠1=∠4=35°,
∵∠2=90°,
∴∠4+∠5=90°,
∴∠5=55°,
∴∠3=180°-∠5=125°,
故选:A.
点睛:本题考查平行线的性质、三角形内角和定理,邻补角的性质等知识,解题的关键是灵活运用所学知识解决问题.
9.35
【解析】
分析:
根据“平行线的判定和性质”结合“已知条件”分析解答即可.
详解:
∵∠1=∠2,
∴AB∥CE,
∴∠3=∠B=35°.
故答案为35.
点睛:熟记“平行线的判定方法和性质”是解答本题的关键.
10.
【解析】
【分析】
由已知角互补及邻补角定义,得到一对同位角相等,利用同位角相等两直线平行得到EF与AB平行,利用两直线平行内错角相等得到一对角相等,根据已知角相等,等量代换得到一对同位角相等,利用同位角相等两直线平行得到DE与AC平行,利用两直线平行同位角相等即可求出所求角的度数.
【详解】
解:∵∠1+∠2=180°,∠2+∠BDC=180°,
∴∠BDC=∠1,
∴EF∥AB,
∴∠DEF=∠BDE,
∵∠DEF=∠A,
∴∠BDE=∠A,
∴DE∥AC,
∴∠ACB=∠BED=70°.
【点睛】
此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
11.
【解析】
【分析】
根据平行线的性质结合三角板的角的度数即可求得答案.
【详解】
,
,
故答案为:.
【点睛】
本题考查了平行线的性质,熟练掌握两直线平行,内错角相等是解题的关键.
12.105°
【解析】
【分析】
如图,根据邻补角的定义求出∠3的度数,继而根据平行线的性质即可求得答案.
【详解】
∵∠1+∠3=180°,∠1=75°,
∴∠3=105°,
∵a//b,
∴∠2=∠3=105°,
故答案为:105°.
【点睛】
本题考查了邻补角的定义,平行线的性质,熟练掌握两直线平行,内错角相等是解本题的关键.
13.55°
【解析】
【分析】
根据平行的性质,同旁内角互补和垂直列出等式,即可得解.
【详解】
∵AB∥CD,
∴∠BAC+∠ACD=180°
∴∠1+∠2+∠CAE=180°
∵AE⊥AC,∠2=35°,
∴∠1=180°-35°-90°=55°
故答案为:55°.
【点睛】
此题主要考查平行线的性质,熟练掌握,即可解题.
14.55
【解析】
【分析】
根据对顶角相等的性质可知∠1的对顶角的度数,再根据平行线的性质可知同旁内角互补,从而可求答案.
【详解】
∵
∴∠2+∠3=180°
又∵∠1=∠3=125°
∴∠2=180°-∠3=180°-125°=55°
故答案为55.
【点睛】
本题考查的是对顶角的性质和平行线的性质,知道两直线平行同旁内角互补是解题的关键.
15.见解析
【解析】
【分析】
利用平行线的性质定理可得∠BOD=∠B,等量代换可得∠BOD+∠D=180°,利用同旁内角互补,两直线平行可得结论.
【详解】
证明:∵CD∥BF, ∴∠BOD=∠B, ∵∠B+∠D=180°, ∴∠BOD+∠D=180°, ∴AB∥DE.
【点睛】
考查了平行线的性质定理和判定定理,综合运用定理是解答此题的关键.
16.(1)证明见解析(2)
【解析】
【分析】
(1)根据平行线的性质和等量代换即可证明;(2)先求出∠EDF=∠2=70°,再根据角平分线和平行线的性质即可得出∠C的度数.
【详解】
(1)∵DE∥AB,∴∠A=∠2,
∵∠1+∠2=180°,∴∠A+∠1=180°,∴DF∥AC
(2)∵∠1=110°,
∴∠2=70°,
∵AC∥DF,∴∠FDE=∠2=70°,
∵DF平分∠BDE,
∴∠BDF=70°,∴∠C=∠BDF=70°.
【点睛】
此题主要考查平行线的判定与性质,解题的关键是熟知平行线的性质.
17.两直线平行,同旁内角互补;∠ADC;两直线平行,同旁内角互补;同角的补角相等;角的平分线的定义;∠1;两直线平行,内错角相等;同位角相等,两直线平行.
【解析】
【分析】
先由平行线的性质知∠ABC+∠C=∠ADC+∠C=180°知∠ABC=∠ADC,根据角平分线的定义证∠1=∠2,结合AD∥BC得∠2=∠3,根据平行线的性质得∠1=∠3,从而得证.
【详解】
证明:∵AB∥CD,(已知) ∴∠ABC+∠C=180°.(两直线平行,同旁内角互补) 又∵AD∥BC,(已知) ∴∠ADC+∠C=180°.(两直线平行,同旁内角互补) ∴∠ABC=∠ADC.(同角的补角相等) ∵BE平分∠ABC,(已知) ∴∠1=∠ABC.(角的平分线的定义) 同理,∠2=∠ADC. ∴∠1=∠2. ∵AD∥BC,(已知) ∴∠2=∠3.(两直线平行,内错角相等) ∴∠1=∠3, ∴BE∥DF.(同位角相等,两直线平行) 故答案为:两直线平行,同旁内角互补;∠ADC;两直线平行,同旁内角互补;同角的补角相等;角的平分线的定义;∠1;两直线平行,内错角相等;同位角相等,两直线平行.
【点睛】
本题考查的是平行线的判定与性质,熟知平行线的判定定理与性质定理是解答此题的关键.
18.(1)详见解析;(2)70°.
【解析】
【分析】
(1)先证出∠2=∠DFE,再得出EF∥AB;
(2)由平行线的性质得出∠BDE=∠DEF,再证出∠BDE=∠A.得出DE∥AC,由平行线的性质即可得出结果.
【详解】
解:(1)证:∵∠1+∠DFE=180°,
∴∠1+∠2=180°.
∴∠DFE=∠2,
∴EF//AB;
(2)∵EF//AB,
∴∠DEF=∠BDE.
又∵∠DEF=∠A,
∴∠BDE=∠A,
∴DE//AC,
∴∠ACB=∠DEB.
又∵∠DEB =70°,
∴∠ACB=70°.
【点睛】
此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质定理是解题的关键.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,在ΔABC中,D、 E、F分别在AB、BC、AC上,且EF∥AB,要使DF∥BC,只需再有下列条件中的( )即可.
A.∠1=∠2 B.∠1=∠DFE C.∠1=∠AFD D.∠2=∠AFD
2.如图,已知,为角平分线,下列说法错误的是( )
A. B. C. D.
3.如图,已知∥,且∠1=120°,则∠2=( )
A.40° B.50° C.60° D.70°
4.将等腰直角三角形纸片和矩形纸片按如图方式折叠放在一起,若,则的度数为( )
A. B. C. D.
5.如图是婴儿车的平面示意图,其中AB∥CD,∠1=120°,∠3=40°,那么∠2的度数为( )
A.80° B.90° C.100° D.102°
6.如图,已知直线a∥b,直线c与a,b相交,∠1=110°,则∠2的度数为( )
A.60° B.70°
C.80° D.110°
7.如图,∥,点在直线上,且,,那么的度数是( )
A. B. C. D.
8.如图所示,直线a∥b,∠1=35°,∠2=90°,则∠3的度数为( )
A.125° B.135° C.145° D.155°
二、填空题
9.如图,已知∠1=∠2,∠B=35°,则∠3=________°.
10.如图,在中,已知,,,则的度数为__________.
11.已知直线,将一块含角的直角三角板ABC按如图所示方式放置(),并且顶点A,C分别落在直线a,b上,若,则的度数是______.
12.如图,已知,,则_____.
13.如图,AB∥CD,AE⊥AC交CD于点E,若∠2=35°,则∠1=______.
14.如图,直线,则_____________度
三、解答题
15.如图,已知CD∥BF, ∠B+∠D=180°,求证:AB∥DE.
16.如图,D、E、F分别在△ABC的三条边上,DE∥AB,∠1+∠2=180°.
(1)试说明:DF∥AC;
(2)若∠1=110°,DF平分∠BDE,求∠C的度数.
17.完成下面的证明过程:
如图,AB∥CD,AD∥BC,BE平分∠ABC,DF平分∠ADC.
求证:BE∥DF.
证明:∵AB∥CD,(已知)
∴∠ABC+∠C=180°.( )
又∵AD∥BC,(已知)
∴ +∠C=180°.( )
∴∠ABC=∠ADC.( )
∵BE平分∠ABC,(已知)
∴∠1=∠ABC.( )
同理,∠2=∠ADC.
∴ =∠2.
∵AD∥BC,(已知)
∴∠2=∠3.( )
∴∠1=∠3,
∴BE∥DF.( )
18.如图,,,.
(1)求证::
(2)求的度数.
参考答案
1.B
【解析】
∵EF∥AB,∴∠1=∠2(两直线平行,同位角相等).∵∠1=∠DFE,
∴∠2=∠DFE(等量代换),∴DF∥BC(内错角相等,两直线平行).
所以只需满足下列条件中的∠1=∠DFE.故选B.
2.B
【解析】
【分析】
利用平行线的性质得到∠2=∠4,∠3=∠2,∠5=∠1+∠2,再根据角平分线的定义得到∠1=∠2=∠4=∠3,∠5=2∠1,从而可对各选项进行判断.
【详解】
∵l1∥AB,
∴∠2=∠4,∠3=∠2,∠5=∠1+∠2,
∵AC为角平分线,
∴∠1=∠2=∠4=∠3,∠5=2∠1.
故选B.
【点睛】
本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.
3.C
【解析】
【分析】
先利用平行线的性质求出∠3的度数,再利用邻补角的定义即可求出答案.
【详解】
∵l1∥l2,
∴∠3=∠1=120°,
∴∠2=180°-∠3=60°,
故选C.
【点睛】
本题考查了平行线的性质及邻补角的定义.通过添加∠3形成同位角是解题的关键.
4.B
【解析】
【分析】
根据平行的性质即可求解.
【详解】
根据平行线的性质得到∠3=∠1=30°,
∴∠2=45°-∠3=15°.
以及等腰直角三角形的性质,故选B
【点睛】
此题主要考查平行线的性质,解题的关键是熟知两直线平行,内错角相等.
5.A
【解析】
分析:根据平行线性质求出∠A,根据三角形内角和定理得出∠2=180°∠1?∠A,代入求出即可.
详解:∵AB∥CD.
∴∠A=∠3=40°,
∵∠1=60°,
∴∠2=180°∠1?∠A=80°,
故选:A.
点睛:本题考查了平行线的性质:两直线平行,内错角相等.三角形内角和定理:三角形内角和为180°.
6.B
【解析】
【分析】
直接根据平行线的性质即可得出结论.
【详解】
∵直线a∥b,
∴∠3=∠1=110°,
∴∠2=180°?110°=70°,
故答案选B.
【点睛】
本题考查的知识点是平行线的性质,解题的关键是熟练的掌握平行线的性质.
7.B
【解析】
【分析】
由题意,求出∠3的度数,然后由∥,即可得到∠2的度数.
【详解】
解:如图:
∵,
∴∠ABC=90°,
∵,
∴,
∵∥,
∴;
故选:B.
【点睛】
本题考查了平行线的性质和角的运算,解题的关键是正确求出∠3的度数.
8.A
【解析】
分析:如图求出∠5即可解决问题.
详解:
∵a∥b,
∴∠1=∠4=35°,
∵∠2=90°,
∴∠4+∠5=90°,
∴∠5=55°,
∴∠3=180°-∠5=125°,
故选:A.
点睛:本题考查平行线的性质、三角形内角和定理,邻补角的性质等知识,解题的关键是灵活运用所学知识解决问题.
9.35
【解析】
分析:
根据“平行线的判定和性质”结合“已知条件”分析解答即可.
详解:
∵∠1=∠2,
∴AB∥CE,
∴∠3=∠B=35°.
故答案为35.
点睛:熟记“平行线的判定方法和性质”是解答本题的关键.
10.
【解析】
【分析】
由已知角互补及邻补角定义,得到一对同位角相等,利用同位角相等两直线平行得到EF与AB平行,利用两直线平行内错角相等得到一对角相等,根据已知角相等,等量代换得到一对同位角相等,利用同位角相等两直线平行得到DE与AC平行,利用两直线平行同位角相等即可求出所求角的度数.
【详解】
解:∵∠1+∠2=180°,∠2+∠BDC=180°,
∴∠BDC=∠1,
∴EF∥AB,
∴∠DEF=∠BDE,
∵∠DEF=∠A,
∴∠BDE=∠A,
∴DE∥AC,
∴∠ACB=∠BED=70°.
【点睛】
此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
11.
【解析】
【分析】
根据平行线的性质结合三角板的角的度数即可求得答案.
【详解】
,
,
故答案为:.
【点睛】
本题考查了平行线的性质,熟练掌握两直线平行,内错角相等是解题的关键.
12.105°
【解析】
【分析】
如图,根据邻补角的定义求出∠3的度数,继而根据平行线的性质即可求得答案.
【详解】
∵∠1+∠3=180°,∠1=75°,
∴∠3=105°,
∵a//b,
∴∠2=∠3=105°,
故答案为:105°.
【点睛】
本题考查了邻补角的定义,平行线的性质,熟练掌握两直线平行,内错角相等是解本题的关键.
13.55°
【解析】
【分析】
根据平行的性质,同旁内角互补和垂直列出等式,即可得解.
【详解】
∵AB∥CD,
∴∠BAC+∠ACD=180°
∴∠1+∠2+∠CAE=180°
∵AE⊥AC,∠2=35°,
∴∠1=180°-35°-90°=55°
故答案为:55°.
【点睛】
此题主要考查平行线的性质,熟练掌握,即可解题.
14.55
【解析】
【分析】
根据对顶角相等的性质可知∠1的对顶角的度数,再根据平行线的性质可知同旁内角互补,从而可求答案.
【详解】
∵
∴∠2+∠3=180°
又∵∠1=∠3=125°
∴∠2=180°-∠3=180°-125°=55°
故答案为55.
【点睛】
本题考查的是对顶角的性质和平行线的性质,知道两直线平行同旁内角互补是解题的关键.
15.见解析
【解析】
【分析】
利用平行线的性质定理可得∠BOD=∠B,等量代换可得∠BOD+∠D=180°,利用同旁内角互补,两直线平行可得结论.
【详解】
证明:∵CD∥BF, ∴∠BOD=∠B, ∵∠B+∠D=180°, ∴∠BOD+∠D=180°, ∴AB∥DE.
【点睛】
考查了平行线的性质定理和判定定理,综合运用定理是解答此题的关键.
16.(1)证明见解析(2)
【解析】
【分析】
(1)根据平行线的性质和等量代换即可证明;(2)先求出∠EDF=∠2=70°,再根据角平分线和平行线的性质即可得出∠C的度数.
【详解】
(1)∵DE∥AB,∴∠A=∠2,
∵∠1+∠2=180°,∴∠A+∠1=180°,∴DF∥AC
(2)∵∠1=110°,
∴∠2=70°,
∵AC∥DF,∴∠FDE=∠2=70°,
∵DF平分∠BDE,
∴∠BDF=70°,∴∠C=∠BDF=70°.
【点睛】
此题主要考查平行线的判定与性质,解题的关键是熟知平行线的性质.
17.两直线平行,同旁内角互补;∠ADC;两直线平行,同旁内角互补;同角的补角相等;角的平分线的定义;∠1;两直线平行,内错角相等;同位角相等,两直线平行.
【解析】
【分析】
先由平行线的性质知∠ABC+∠C=∠ADC+∠C=180°知∠ABC=∠ADC,根据角平分线的定义证∠1=∠2,结合AD∥BC得∠2=∠3,根据平行线的性质得∠1=∠3,从而得证.
【详解】
证明:∵AB∥CD,(已知) ∴∠ABC+∠C=180°.(两直线平行,同旁内角互补) 又∵AD∥BC,(已知) ∴∠ADC+∠C=180°.(两直线平行,同旁内角互补) ∴∠ABC=∠ADC.(同角的补角相等) ∵BE平分∠ABC,(已知) ∴∠1=∠ABC.(角的平分线的定义) 同理,∠2=∠ADC. ∴∠1=∠2. ∵AD∥BC,(已知) ∴∠2=∠3.(两直线平行,内错角相等) ∴∠1=∠3, ∴BE∥DF.(同位角相等,两直线平行) 故答案为:两直线平行,同旁内角互补;∠ADC;两直线平行,同旁内角互补;同角的补角相等;角的平分线的定义;∠1;两直线平行,内错角相等;同位角相等,两直线平行.
【点睛】
本题考查的是平行线的判定与性质,熟知平行线的判定定理与性质定理是解答此题的关键.
18.(1)详见解析;(2)70°.
【解析】
【分析】
(1)先证出∠2=∠DFE,再得出EF∥AB;
(2)由平行线的性质得出∠BDE=∠DEF,再证出∠BDE=∠A.得出DE∥AC,由平行线的性质即可得出结果.
【详解】
解:(1)证:∵∠1+∠DFE=180°,
∴∠1+∠2=180°.
∴∠DFE=∠2,
∴EF//AB;
(2)∵EF//AB,
∴∠DEF=∠BDE.
又∵∠DEF=∠A,
∴∠BDE=∠A,
∴DE//AC,
∴∠ACB=∠DEB.
又∵∠DEB =70°,
∴∠ACB=70°.
【点睛】
此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质定理是解题的关键.
