浙江省宁波市镇海中学2019-2020学年高二上学期期中考试数学试题
文档属性
| 名称 | 浙江省宁波市镇海中学2019-2020学年高二上学期期中考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-22 13:03:00 | ||
图片预览




文档简介
2019学年镇海中学高二上期中
一、选择题:每小题4分,共40分
1.方程表示的曲线是( )
A.一条射线 B.双曲线
C.双曲线的左支 D.双曲线的右支
2.设x∈R,则“x>1”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.“红豆生南国,春来发几枝.愿君多采撷,此物最相思.”这是唐代诗人王维的《相思》诗,在这4句诗中,哪句可作为命题( )
A.红豆生南国 B.春来发几枝 C.愿君多采撷 D.此物最相思
4.已知m,n表示两条不同直线,α,β表示两个不同的平面,以下能判定m⊥α的是( )
A.α⊥β且m?β B.α⊥β且m∥β C.α∥β且m⊥β D.m⊥n且n∥α
5.在空间直角坐标系O﹣xyz中,O为坐标原点,若点P(1,﹣2,3)在平面xOz上的投影为点B,则线段OB的长度为( )
A. B. C. D.
6.下列有关命题的说法正确的是( )
A.命题“若⊥,则?0”的否命题为“若⊥,则?0”
B.命题“函数f(x)=(a﹣1)x是R上的增函数”的否定是“函数f(x)=(a﹣1)x是R上的减函数”
C.命题“在△ABC中,若sinA=sinB,则A=B”的逆否命题为真命题
D.命题“若x=2,则x2﹣3x+2=0”的逆命题为真命题
7.已知正方体ABCD﹣A1B1C1D1,点E为平面BCC1B1的中心,则直线DE与平面ACD1所成角的余弦值为( )
A. B. C. D.
8.设双曲线的上焦点为F,过点F作与y轴垂直的直线交两渐近线于A,B两点,且与双曲线在第一象限的交点为P,设O为坐标原点,若,,则双曲线的离心率e的值是( )
A.3 B. C. D.
9.设抛物线y2=8x的焦点为F,经过定点P(a,0)(a>0)的直线l与抛物线交于A,B两点,且,|AF|+2|BF|=9,则a=( )
A.1 B.2 C.3 D.4
10.四棱锥P﹣ABCD中,已知,|AB|=|AD|=a,|AP|=b,|PC|=1,则b的最大值为( )
A. B. C. D.
二、填空题:单空题每题4分,多空题每题6分
11.双曲线的渐近线方程为 ,焦点坐标为 .
12.已知,.若,则μ= ;若,则λ+μ= .
13.已知向量,,是空间的一组单位正交基底,向量,,是空间的另一组基底,若向量在基底,,下的坐标为(2,1,3),p在基底,,下的坐标为(x,y,z),则x﹣y= ,z= .
14.若动点P到点F(0,1)的距离比它到直线y=﹣2的距离少1,则动点P的轨迹C的方程为 ,若过点(2,1)作该曲线C的切线l,则切线l的方程为 .
15.在四面体ABCD中,△ABD和△BCD均为等边三角形,AB=2,,则二面角B﹣AD﹣C的余弦值为 .
16.四边形ABCD的各个顶点依次位于抛物线y=x2上,∠BAD=60°,对角线AC平行x轴,且AC平分∠BAD,若,则ABCD的面积为 .
17.已知椭圆E:,点A,B分别是椭圆E的左顶点和上顶点,直线AB与圆C:x2+y2=c2相离,其中c是椭圆的半焦距,P是直线AB上一动点,过点P作圆C的两条切线,切点分别为M,N,若存在点P使得△PMN是等腰直角三角形,则椭圆离心率平方e2的取值范围是 .
三、解答题:5小题,共74分
18.已知a>0,且a≠1.命题P:函数f(x)=logax在(0,+∞)上为增函数;命题Q:函数g(x)=x2﹣2ax+4有零点.
(1)若命题P,Q满足P真Q假,求实数a的取值范围;
(2)命题S:函数y=f(g(x))在区间[2,+∞)上值恒为正数.若命题S为真命题,求实数a的取值范围.
19.如图,在四棱锥P﹣ABCD中,四边形ABCD是菱形,,BD=2.
(1)若点E,F分别为线段PD,BC上的中点,求证:EF∥平面PAB;
(2)若平面PBD⊥平面ABCD,且PD⊥PB,PD=PB,求平面PAB与平面PBC所成的锐二面角的余弦值.
20.如图,已知椭圆,过动点M(0,m)的直线交x轴于点N,交椭圆C于A,P(其中P在第一象限,N在椭圆内),且M是线段PN的中点,点P关于x轴的对称点为Q,延长QM交C于点B,记直线PM,QM的斜率分别为k1,k2.
(1)当时,求k2的值;
(2)当时,求直线AB斜率的最小值.
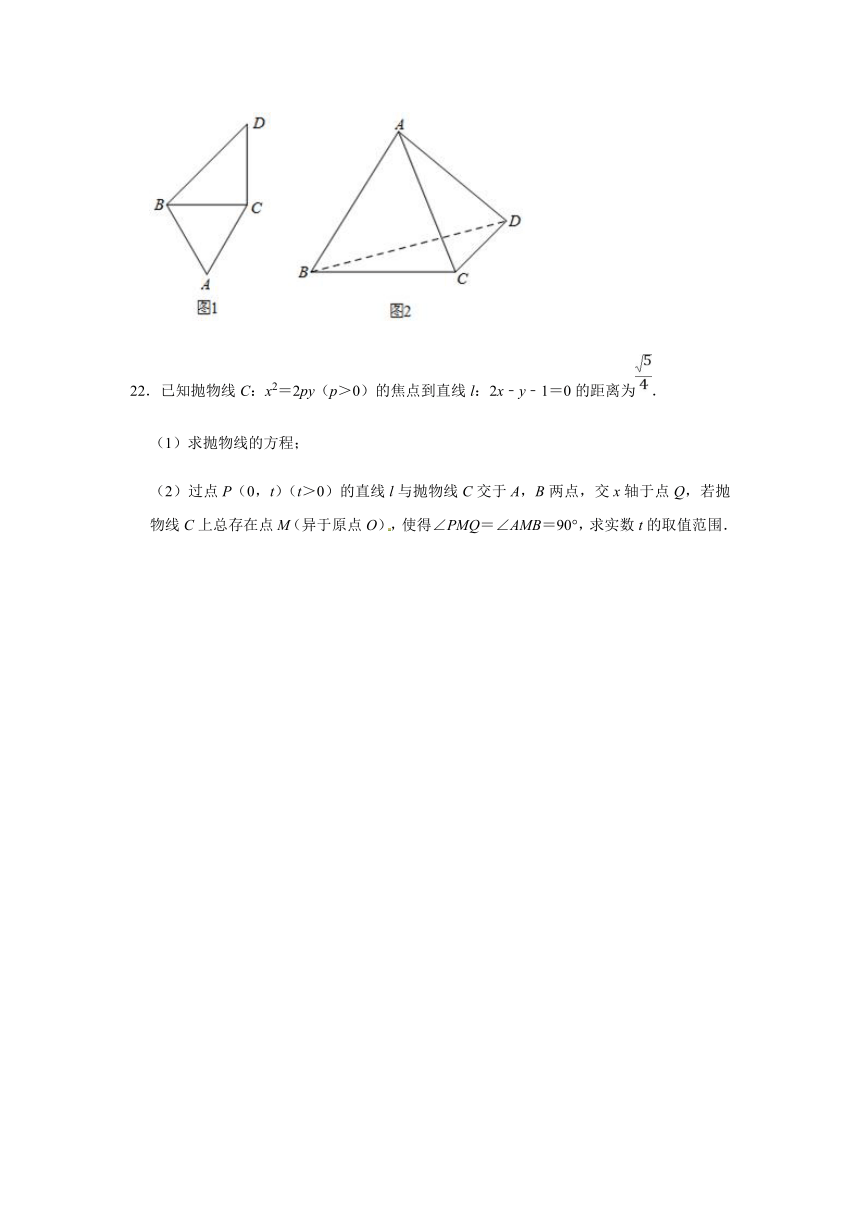
21.如图,△ABC为正三角形,且BC=CD=2,CD⊥BC,将△ABC沿BC翻折.
(1)当AD=2时,求证:平面ABD⊥平面BCD;
(2)若点A的射影在△BCD内,且直线AB与平面ACD所成角为60°,求AD的长.
22.已知抛物线C:x2=2py(p>0)的焦点到直线l:2x﹣y﹣1=0的距离为.
(1)求抛物线的方程;
(2)过点P(0,t)(t>0)的直线l与抛物线C交于A,B两点,交x轴于点Q,若抛物线C上总存在点M(异于原点O),使得∠PMQ=∠AMB=90°,求实数t的取值范围.
一、选择题:每小题4分,共40分
1.D
2.A
3.A
4.C
5.B
6.C
7.B
8.C
9.A
10.B
二、填空题:单空题每题4分,多空题每题6分
11. yx;(±2,0).
12. ,.
13. 1,3.
14.解(1)设动点P的坐标为(x,y),由题意可知:;
∴x2=4y;
动点P的轨迹C方程为x2=4y;
(2)设过点(2,1)的直线方程为y=k(x﹣2)+1;
①当k不存在时,则直线方程为x=2,与曲线C不相切;
②当k存在时,联立,
∴x2﹣4kx+8k﹣4=0.
∵直线与曲线C相切,
∴△=16k2﹣32k+16=0;
解得:k=1;
切线l的方程为y=x﹣1.
15. .
16. .
17.由题意,AB所在直线方程为,即bx﹣ay+ab=0,
又直线AB与圆C:x2+y2=c2相离,∴c,
即a2b2>c2(a2+b2),∴a2(a2﹣c2)>c2(2a2﹣c2),
整理得:e4﹣3e2+1>0,解得0<e2;
又存在点P使得△PMN是等腰直角三角形,
则在Rt△OPN中,OPONc,
∴,即a2b2≤2c2(a2+b2),
∴a2(a2﹣c2)≤2c2(2a2﹣c2),
整理得2e4﹣5e2+1≤0,解得e2<1.
∴e2的取值范围是[,).
三、解答题:5小题,共74分
18.(1)由命题P:函数f(x)=logax在(0,+∞)上为增函数是真,得a>1;
由命题Q:函数g(x)=x2﹣2ax+4有零点为假,得△=4a2﹣16<0,得﹣2<a<2.
∴使命题P真Q假的实数a的取值范围是(1,2);
(2)若函数y=f(g(x))在区间[2,+∞)上值恒为正数,
则首先保证g(x)=x2﹣2ax+4在[2,+∞)上恒大于0,
则△=4a2﹣16<0或,
得﹣2<a<2.
又a>0且a≠1,∴0<a<2且a≠1.
当0<a<1时,外层函数f(x)单调递减,而内层函数g(x)当x→+∞时,g(x)→+∞,
此时y=f(g(x))<0,不合题意;
当1<a<2时,外层函数f(x)单调递增,要使y=f(g(x))>0在区间[2,+∞)上恒成立,
则g(x)=x2﹣2ax+4在[2,+∞)上的最小值大于1.
即g(2)=8﹣4a>1,得a.
∴1<a.
即使命题S为真命题的实数a的取值范围是(1,).
19.(1)取AP得中点为H,连接EH,HB;
由E,H分别为PD,PA的中点,则EH∥AD且;
又F为BC的中点,则BF∥AD且;
所以EH∥BF且EH=BF,则四边形BFEH为平行四边形;
所以EF∥BH,又HB?平面PAB;
所以EF∥平面PAB;
(2)过A作AN⊥PB于点N,连接NC,AC,BD,设AC交BD于点O
在△PBD中O为AC的中点,PD=PB,则PO⊥BD;
又平面PBD⊥平面ABCD,所以PO⊥平面ABCD;
在△PBD中,PD⊥PB,BD=2.则PD=PB;
由题意有PA=PC,AO=2,,
在等腰三角形APB中,;
由△PAB≌△PCB,则CN⊥PB;CN=AN
则∠ANC 为二面角A﹣PB﹣C 的平面角;
在△ACN中,;
故平面PAB与平面PBC所成的锐二面角的余弦值为.
20.(1)设P(x0,y0) (x0>0,y0>0)
M(0,m),可得P(x0,2m),Q(x0,﹣2m).
所以直线PM的斜率;
直线QM的斜率;
此时.当时k2=1;
(2)设A(x1,y1),B(x2,y2).
直线PA的方程为y=kx+m,(k>0)
由,得(1+3k2)x2+6kmx+3m2﹣3=0
,即;
所以;
直线QB的方程为y=﹣3kx+m.
同理有:,,
2,
当且仅当,即时取等号;
故直线AB 的斜率的最小值为1.
21.(1)证明:若AD=2,又AB=AC=2,
则A在底面BCD内的射影为△BCD的外心,
∵△BCD为直角三角形,且∠BCD=90°,
∴A在底面BCD内的射影E落在BD的中点上,
∴AE⊥平面BCD,而AE?平面ABD,
∴平面ABD⊥平面BCD;
(2)解:取BC中点O,BD中点E,连接AO,OE,
可得BC⊥平面AOE,过A作AH⊥OE于H,过H作HN∥BC交CD于N,
连接AN,作HQ⊥AN于Q,得HQ⊥平面ACD,
点B到平面ACD的距离为2HQ,则sin60,
得HQ,
设AH=x,有,解得x,即AH,
又AO,∴H与O重合,
则AD.
22.(1)抛物线C:x2=2py(p>0)的焦点(0,)到直线l:2x﹣y﹣1=0的距离为,
可得,解得p,即抛物线的方程为x2=y;
(2)过点P(0,t)(t>0)的直线l的方程设为y=kx+t,联立x2=y,可得x2﹣kx﹣t=0,
设A(x1,y1),B(x2,y2),可得k2+4t>0,x1+x2=k,x1x2=﹣t,且y1=x12,y2=x22,
设M(m,m2),Q(,0),
由∠PMQ=∠AMB=90°,可得?1,化为m3﹣mt+m,①
?1,即(m+x1)(m+x2)=﹣1,化为m2+km﹣t+1=0,②
由①②可得t=k2m2,
由k2﹣4(1﹣t)≥0可得4(1﹣t)≤k2,
由于m≠0,m2>0,可得0解得t≥1.
