人教版七年级数学下册5.1.3 同位角、内错角、同旁内角课件(共21张PPT)
文档属性
| 名称 | 人教版七年级数学下册5.1.3 同位角、内错角、同旁内角课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 324.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-21 10:20:36 | ||
图片预览




文档简介
课件21张PPT。人教版 数学七年级下册第五章 相交线与平行线5.1.3 同位角、内错角、同旁内角前言学习目标
1、理解同位角、内错角、同旁内角的概念。 2、在简单几何图形中指出同位角、内错角、同旁内角。 3、通过观察、探究,培养学生观察图形的能力。
重点
理解同位角、内错角、同旁内角的概念。
难点
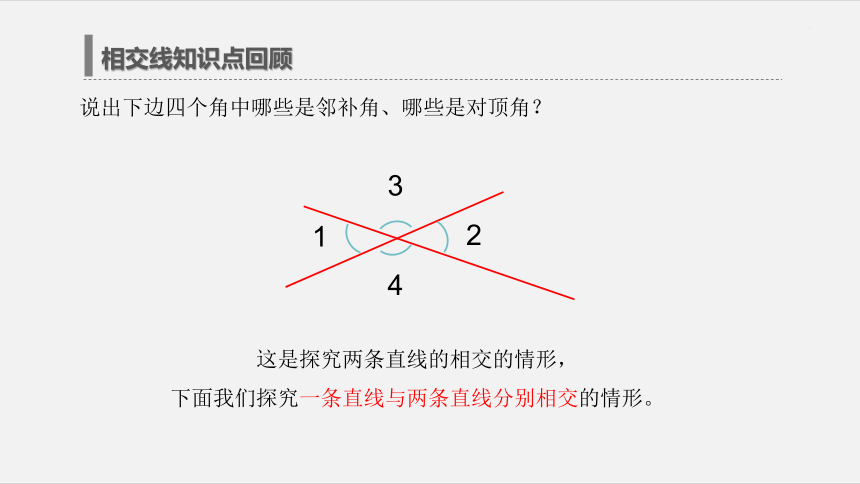
辨别同位角、内错角、同旁内角。相交线知识点回顾邻补角的概念:对顶角的概念:对顶角的性质:如果两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角。如果两个角有一个公共顶点,并且它们的两边分别互为反向延长线,那么这两个角叫对顶角。对顶角相等相交线知识点回顾说出下边四个角中哪些是邻补角、哪些是对顶角?这是探究两条直线的相交的情形,
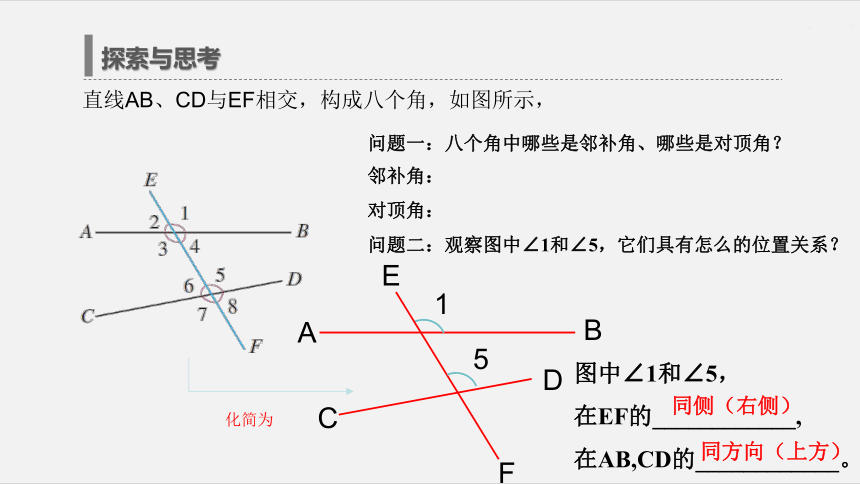
下面我们探究一条直线与两条直线分别相交的情形。探索与思考直线AB、CD与EF相交,构成八个角,如图所示,问题一:八个角中哪些是邻补角、哪些是对顶角?
邻补角:
对顶角:
问题二:观察图中∠1和∠5,它们具有怎么的位置关系?化简为图中∠1和∠5,
在EF的____________,
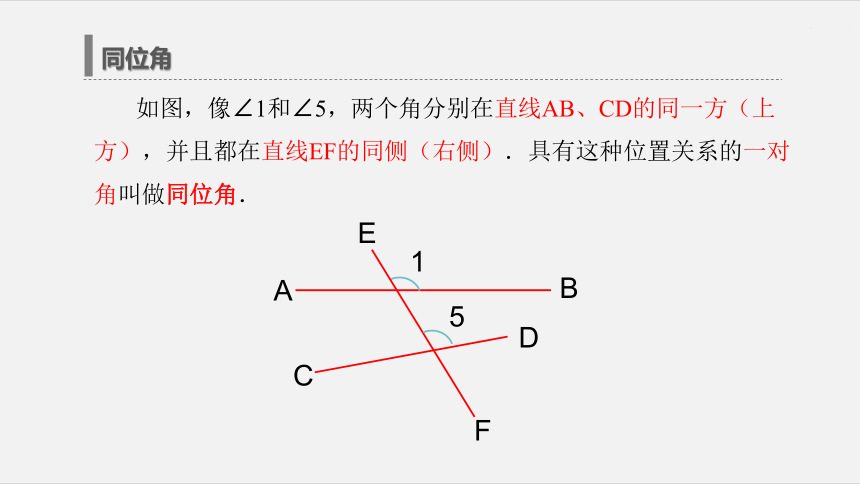
在AB,CD的____________。同侧(右侧)同方向(上方)同位角 如图,像∠1和∠5,两个角分别在直线AB、CD的同一方(上方),并且都在直线EF的同侧(右侧).具有这种位置关系的一对角叫做同位角.探索与思考直线AB、CD与EF相交,构成八个角,如图所示,问题三:指出图中其他几组同位角?化简为图中∠1和∠5,
在EF的____________,
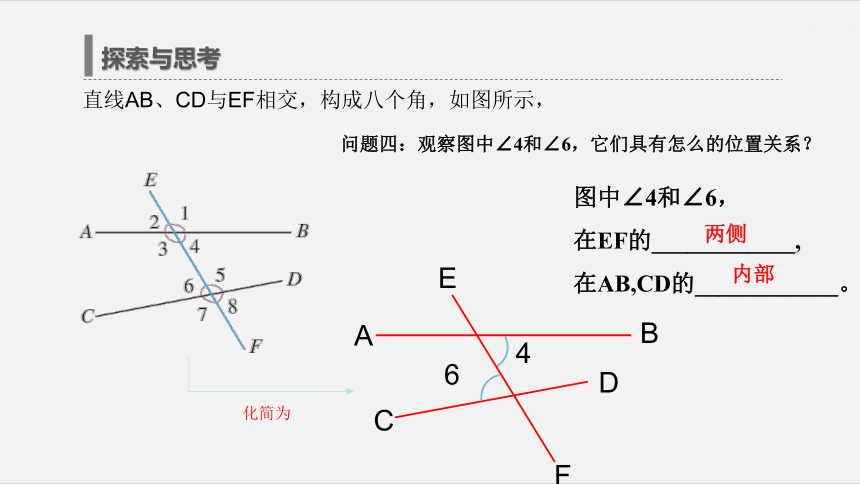
在AB,CD的____________。同侧(右侧)同方向(上方)∠2与∠6,∠3与∠7,∠4与∠8探索与思考直线AB、CD与EF相交,构成八个角,如图所示,问题四:观察图中∠4和∠6,它们具有怎么的位置关系?化简为图中∠4和∠6,
在EF的____________,
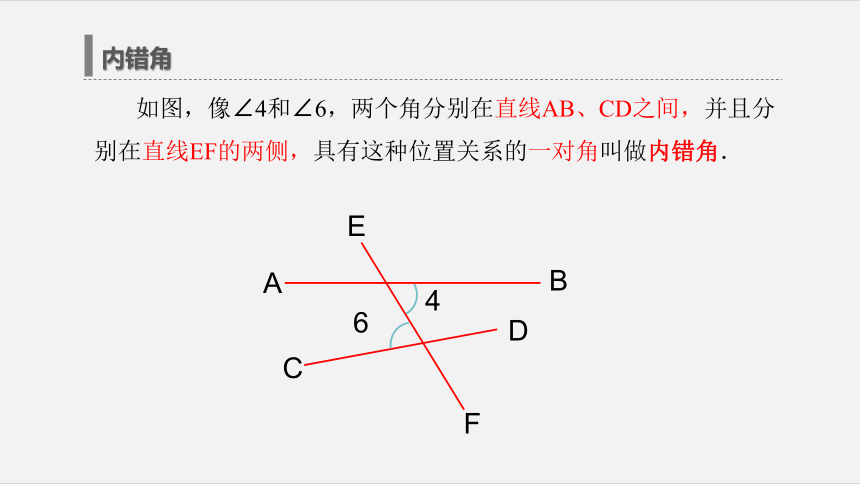
在AB,CD的____________。两侧内部内错角 如图,像∠4和∠6,两个角分别在直线AB、CD之间,并且分别在直线EF的两侧,具有这种位置关系的一对角叫做内错角.探索与思考直线AB、CD与EF相交,构成八个角,如图所示,问题五:指出图中其他几组内错角?化简为图中∠4和∠6,
在EF的____________,
在AB,CD的________。两侧内部∠3与∠5探索与思考直线AB、CD与EF相交,构成八个角,如图所示,问题六:观察图中∠3和∠6,它们具有怎么的位置关系?化简为图中∠3和∠6,
在EF的____________,
在AB,CD的____________。同侧(左侧)内部小结 如图,像∠3和∠6,两个角分别在直线AB、CD之间,并且都在直线EF的同侧,具有这种位置关系的一对角叫做同旁内角.探索与思考直线AB、CD与EF相交,构成八个角,如图所示,问题七:指出图中其他几组同旁内角?化简为图中∠3和∠6,
在EF的____________,
在AB,CD的____________。同侧(左侧)内部∠4 与∠5同位角、内错角、同旁内角总结练一练如图,直线DE、BC被直线AB所截,
1)∠l与∠2,∠1与∠3,∠1与∠4各是什么关系的角?
2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?分别为:内错角、同旁内角、同位角∵ ∠2=∠4而∠1=∠4
∴ ∠1=∠2
∵∠3+∠4=180°而∠1=∠4
∴ ∠3+∠1=180°
∴ ∠1和∠3互补随堂测试?随堂测试2.如图,下列说法错误的是( )
A.∠A与∠AEF是同旁内角 B.∠BED与∠CFG是同位角
C.∠AFE与∠BEF是内错角 D.∠A与∠CFE是同位角【答案】B
【详解】
A. ∠A与∠AEF是同旁内角,正确
B. ∠BED与∠CFG是同位角,错误
C. ∠AFE与∠BEF是内错角,正确
D. ∠A与∠CFE是同位角,正确随堂测试3.(2019·上海市光明中学初一期中)如图,下列判断中,正确的是( )
A.∠2和∠4是同位角 B.∠1和∠B是内错角
C.∠3和∠5是同旁内角 D.∠5和∠B是同旁内角【答案】D
【详解】
A、∠2和∠4无关系;
B、∠1和∠B无关系;
C、∠3和∠5是内错角;
D、∠5和∠B是同旁内角,正确,故选D.随堂测试4.若∠α与∠β同旁内角,且∠α=50°时,则∠β的度数为( )
A.50° B.130° C.50°或130° D.无法确定【答案】D
【详解】
同旁内角只是一种位置关系,并没有一定的大小关系,只有两直线平行时,同旁内角才互补,故选D.课堂互动Classroom Interaction理解同位角概念并判别课后回顾理解内错角概念并判别理解同旁内角概念并判别THANKS“”
1、理解同位角、内错角、同旁内角的概念。 2、在简单几何图形中指出同位角、内错角、同旁内角。 3、通过观察、探究,培养学生观察图形的能力。
重点
理解同位角、内错角、同旁内角的概念。
难点
辨别同位角、内错角、同旁内角。相交线知识点回顾邻补角的概念:对顶角的概念:对顶角的性质:如果两个角有一条公共边,它们的另一边互为反向延长线,具有这种关系的两个角,互为邻补角。如果两个角有一个公共顶点,并且它们的两边分别互为反向延长线,那么这两个角叫对顶角。对顶角相等相交线知识点回顾说出下边四个角中哪些是邻补角、哪些是对顶角?这是探究两条直线的相交的情形,
下面我们探究一条直线与两条直线分别相交的情形。探索与思考直线AB、CD与EF相交,构成八个角,如图所示,问题一:八个角中哪些是邻补角、哪些是对顶角?
邻补角:
对顶角:
问题二:观察图中∠1和∠5,它们具有怎么的位置关系?化简为图中∠1和∠5,
在EF的____________,
在AB,CD的____________。同侧(右侧)同方向(上方)同位角 如图,像∠1和∠5,两个角分别在直线AB、CD的同一方(上方),并且都在直线EF的同侧(右侧).具有这种位置关系的一对角叫做同位角.探索与思考直线AB、CD与EF相交,构成八个角,如图所示,问题三:指出图中其他几组同位角?化简为图中∠1和∠5,
在EF的____________,
在AB,CD的____________。同侧(右侧)同方向(上方)∠2与∠6,∠3与∠7,∠4与∠8探索与思考直线AB、CD与EF相交,构成八个角,如图所示,问题四:观察图中∠4和∠6,它们具有怎么的位置关系?化简为图中∠4和∠6,
在EF的____________,
在AB,CD的____________。两侧内部内错角 如图,像∠4和∠6,两个角分别在直线AB、CD之间,并且分别在直线EF的两侧,具有这种位置关系的一对角叫做内错角.探索与思考直线AB、CD与EF相交,构成八个角,如图所示,问题五:指出图中其他几组内错角?化简为图中∠4和∠6,
在EF的____________,
在AB,CD的________。两侧内部∠3与∠5探索与思考直线AB、CD与EF相交,构成八个角,如图所示,问题六:观察图中∠3和∠6,它们具有怎么的位置关系?化简为图中∠3和∠6,
在EF的____________,
在AB,CD的____________。同侧(左侧)内部小结 如图,像∠3和∠6,两个角分别在直线AB、CD之间,并且都在直线EF的同侧,具有这种位置关系的一对角叫做同旁内角.探索与思考直线AB、CD与EF相交,构成八个角,如图所示,问题七:指出图中其他几组同旁内角?化简为图中∠3和∠6,
在EF的____________,
在AB,CD的____________。同侧(左侧)内部∠4 与∠5同位角、内错角、同旁内角总结练一练如图,直线DE、BC被直线AB所截,
1)∠l与∠2,∠1与∠3,∠1与∠4各是什么关系的角?
2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么?分别为:内错角、同旁内角、同位角∵ ∠2=∠4而∠1=∠4
∴ ∠1=∠2
∵∠3+∠4=180°而∠1=∠4
∴ ∠3+∠1=180°
∴ ∠1和∠3互补随堂测试?随堂测试2.如图,下列说法错误的是( )
A.∠A与∠AEF是同旁内角 B.∠BED与∠CFG是同位角
C.∠AFE与∠BEF是内错角 D.∠A与∠CFE是同位角【答案】B
【详解】
A. ∠A与∠AEF是同旁内角,正确
B. ∠BED与∠CFG是同位角,错误
C. ∠AFE与∠BEF是内错角,正确
D. ∠A与∠CFE是同位角,正确随堂测试3.(2019·上海市光明中学初一期中)如图,下列判断中,正确的是( )
A.∠2和∠4是同位角 B.∠1和∠B是内错角
C.∠3和∠5是同旁内角 D.∠5和∠B是同旁内角【答案】D
【详解】
A、∠2和∠4无关系;
B、∠1和∠B无关系;
C、∠3和∠5是内错角;
D、∠5和∠B是同旁内角,正确,故选D.随堂测试4.若∠α与∠β同旁内角,且∠α=50°时,则∠β的度数为( )
A.50° B.130° C.50°或130° D.无法确定【答案】D
【详解】
同旁内角只是一种位置关系,并没有一定的大小关系,只有两直线平行时,同旁内角才互补,故选D.课堂互动Classroom Interaction理解同位角概念并判别课后回顾理解内错角概念并判别理解同旁内角概念并判别THANKS“”
