1.4 角平分线课件

(共20张PPT)
数学北师大版

八年级
1.4 角平分线
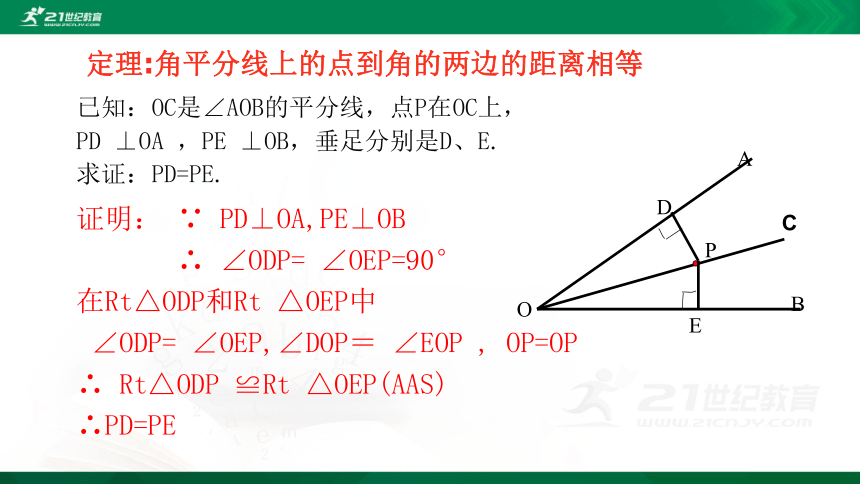
定理:角平分线上的点到角的两边的距离相等
已知：OC是∠AOB的平分线，点P在OC上，
PD ⊥OA ，PE ⊥OB，垂足分别是D、E.
求证：PD=PE.




A
O
B
P
E




D


C
证明： ∵ PD⊥OA,PE⊥OB
∴ ∠ODP= ∠OEP=90°
在Rt△ODP和Rt △OEP中
∠ODP= ∠OEP,∠DOP＝ ∠EOP , OP=OP
∴ Rt△ODP ≌Rt △OEP(AAS)
∴PD=PE
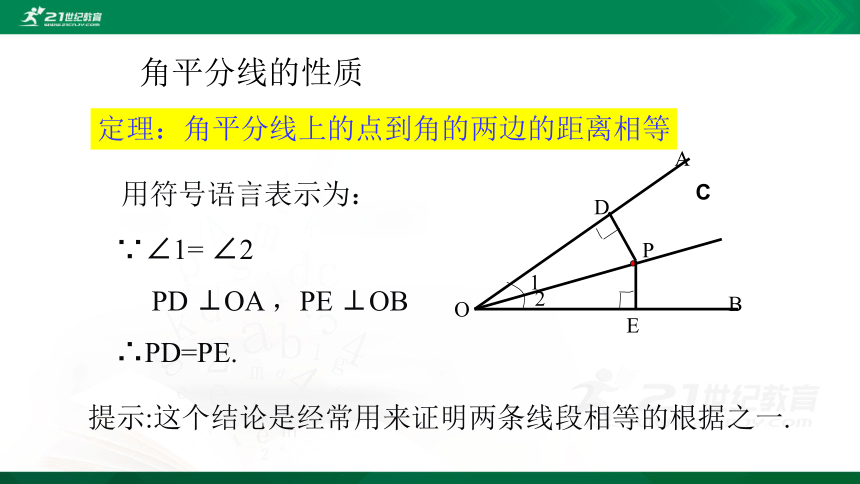
角平分线的性质
定理：角平分线上的点到角的两边的距离相等
用符号语言表示为：




A
O
B
P
E




D



1
2
∵∠1= ∠2
PD ⊥OA ，PE ⊥OB
∴PD=PE.
提示:这个结论是经常用来证明两条线段相等的根据之一.
C
　例.已知：如图，△ABC中，∠C=90°，AD是△ABC的角平分线，DE⊥AB于E，F在AC上,BD=DF.　求证：CF=EB.
证明：∵AD平分∠CAB,
　　DE⊥AB，∠C＝90°（已知）,
∴　CD＝DE (角平分线的性质).
在Rt△CDF和Rt△EDB中,
　　 CD=ED（已证）,
DF=DB （已知）,
∴ Rt△CDF≌Rt△EDB (HL).
∴ CF=EB（全等三角形的对应边相等）.

C
F








A
E
D
B
′


思考分析
你能写出角平分线的性质
定理的逆命题吗?

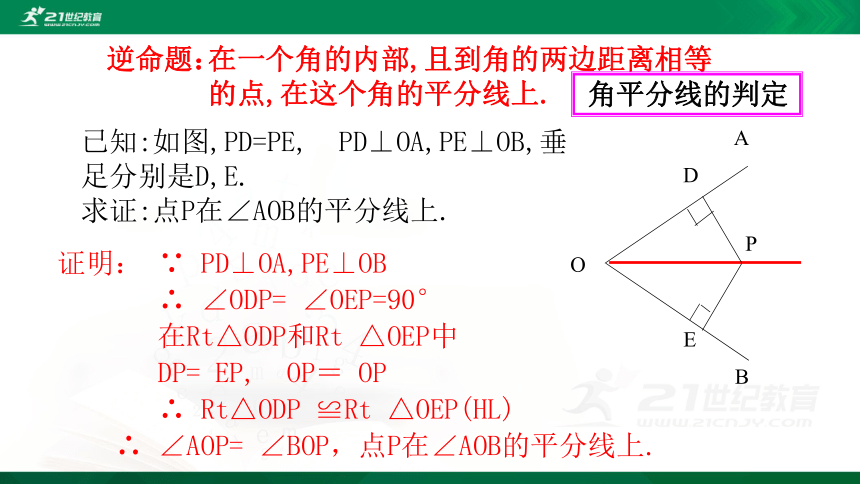
逆命题：
在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.
请你证明它是不是真命题?

已知:如图,PD=PE, PD⊥OA,PE⊥OB,垂足分别是D,E.
求证:点P在∠AOB的平分线上.

O
B
A


P






D
E
逆命题：
在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.
证明： ∵ PD⊥OA,PE⊥OB
∴ ∠ODP= ∠OEP=90°
在Rt△ODP和Rt △OEP中
DP= EP, OP＝ OP
∴ Rt△ODP ≌Rt △OEP(HL)
∴ ∠AOP= ∠BOP，点P在∠AOB的平分线上.

角平分线的判定

O
B
A


P






D
E
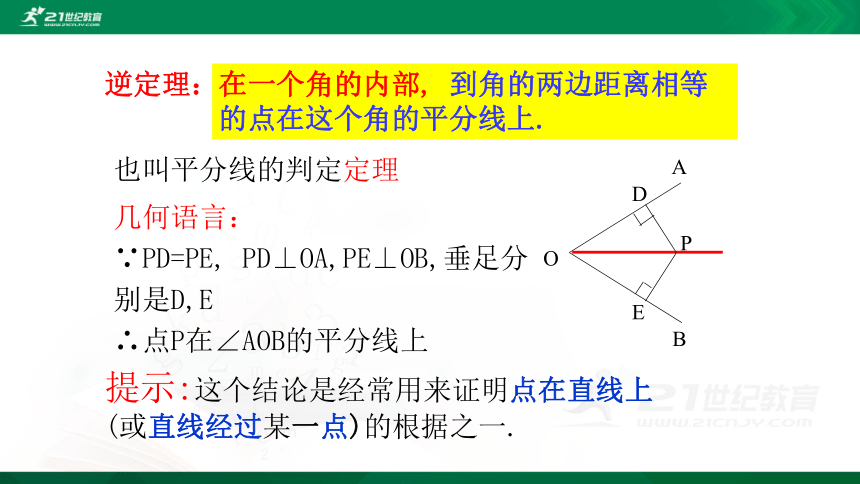
逆定理：
在一个角的内部, 到角的两边距离相等的点在这个角的平分线上.
几何语言：
∵PD=PE, PD⊥OA,PE⊥OB,垂足分别是D,E
∴点P在∠AOB的平分线上
提示:这个结论是经常用来证明点在直线上(或直线经过某一点)的根据之一.

也叫平分线的判定定理
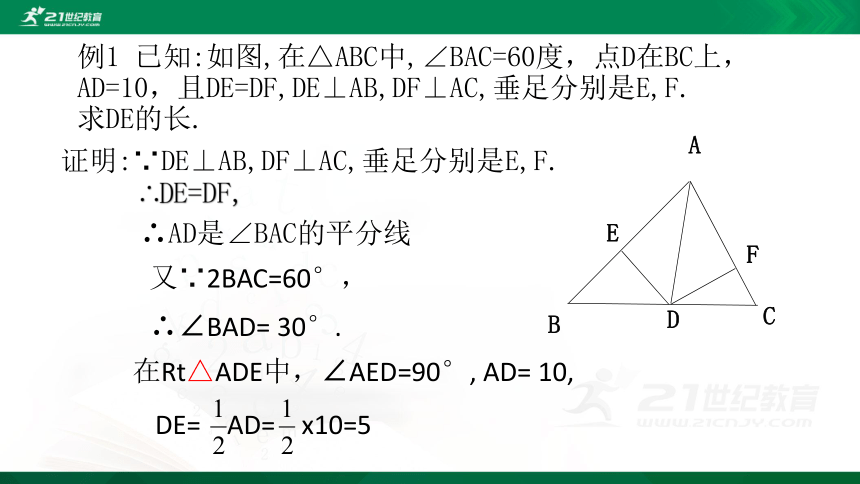
例1 已知:如图,在△ABC中,∠BAC=60度，点D在BC上，AD=10，且DE=DF,DE⊥AB,DF⊥AC,垂足分别是E,F.
求DE的长.






A
B
C
D
E
F
证明:∵DE⊥AB,DF⊥AC,垂足分别是E,F.
∴DE=DF,
∴AD是∠BAC的平分线
又∵2BAC=60°，
∴∠BAD= 30°.
在Rt△ADE中，∠AED=90°, AD= 10,
DE= AD= x10=5
例2　如图,BD=CD,CE⊥AB,BF⊥AC.
求证:∠BAD=∠CAD.
分析:要证明点D在∠BAC的平分线上,只需证明点D到∠BAC两边的距离相等,可以由△BDE≌△CDF得到.
证明:∵CE⊥AB,BF⊥AC,
∴∠BED=∠CFD=90°.
∴△EBD≌△FCD(AAS). ∴DE=DF.
∴点D在∠BAC的平分线上(在一个角的内部,到角的两边距离相等的点在这个角的平分线上).
∴∠BAD=∠CAD.
练习．如图，在四边形ABDC中，∠D＝∠ABD＝90°，点O为BD的中点，且AO平分∠BAC.
求证：OC平分∠ACD.
证明：如图，过点O作OE⊥AC. ∵AO平分∠BAC，∠ABD＝90°， ∴OE＝OB. 又∵点O为BD的中点， ∴OB＝OD， ∴OE＝OD， ∴OC平分∠ACD.







到角的两边的距离相等的点在角的平分线上。
用数学语言表示为：
∵ QD⊥OA，QE⊥OB，QD＝QE．
∴点Q在∠AOB的平分线上．
角的平分线上的点到角的两边的距离相等.
∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上
∴ QD＝QE
本课小结
角平分线的性质定理
角平分线的判定定理
1.如图,在△ABC中,∠C=90° AD是∠BAC的平分线,DE⊥AB于点E,点F在AC上,BD=DF.
求证:(1)CF=EB;
(2)AB=AF+2EB.
证明:(1)∵AD是∠BAC的平分线,DE⊥AB,DC⊥AC, ∴DE=DC. ∵在Rt△DCF和Rt△DEB中,
∴Rt△CDF≌Rt△EDB(HL). ∴CF=EB.






课外作业
BD=DF
DC=DE


2．如图，点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别为C，D.求证： (1)∠ECD＝∠EDC； (2)OC＝OD； (3)OE是线段CD的垂直平分线．
证明：(1)∵点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB， ∴ED＝EC， ∴∠ECD＝∠EDC. (2)∵在Rt△ODE和Rt△OCE中，OE＝OE，ED＝EC
∴Rt△ODE≌Rt△OCE(HL)，∴OC＝OD.






(3)∵ED＝EC，OD＝OC， ∴OE是线段CD的垂直平分线．
3．如图，O是△ABC内一点，且O到△ABC三边AB，BC，CA的距离OF＝OD＝OE，若∠ABC＝60°，∠ACB＝50°，求∠BOC的度数．
解：∵O到三边AB，BC，CA的距离
OF＝OD＝OE， ∴点O是三角形三条角平分线的交点． ∵∠ABC＝60°，∠ACB＝50°， ∴∠OBC＝30°，∠OCB＝25°， ∴∠BOC＝180°－∠OBC－∠OCB ＝180°－30°－25°＝125°.







4.如图，在四边形OACB中,CM⊥OA于点M,若∠1 =∠2,∠3+∠4= 180°
求证:CA=CB.












习题1.9答案
1.解如图,结论:三角形的三个
内角的平分线交于一点,并且
这个点到三角形的三边的距离相等.

2.证明∵AD平分∠BAC且DE⊥AB,DF⊥AC,∴DE=DF.
又BD=DC,∴Rt△BDE≌Rt△CDF(HL).
∴BE=CF.
3.证明证法1:∵∠C=90°,∠A=30°,
∴∠ABC=60°.
∵DE垂直平分AB,∴EA=EB.
∴∠ABE=∠A=30°.
∴∠CBE=∠ABC-∠ABE=30°=∠ABE.
∴BE平分∠ABC.
证法2:∵∠C=90°,∠A=30°,
∴BC= AB∵DE垂直平分AB,
∴BD= AB,∠BDE=90°.
∴BC=BD.
又∵∠C=90°,BE=BE,
∴Rt△BDE≌Rt△BCE(HL).
∴∠DBE=∠CBE
∴BE平分∠ABC.
4.解作法:如图,(1)作∠AOB的平分线OM;
(2)连接CD;
(3)作CD的垂直平分线交OM于点P,则P点即为所求.
谢谢
21世纪教育网（www.21cnjy.com) 中小学教育资源网站
有大把高质量资料？一线教师？一线教研员？
欢迎加入21世纪教育网教师合作团队！！月薪过万不是梦！！
详情请看：
https://www.21cnjy.com/help/help_extract.php