2020春北师大版八下数学2.3不等式的解集教学课件(共22张PPT)
文档属性
| 名称 | 2020春北师大版八下数学2.3不等式的解集教学课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 686.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-21 18:26:43 | ||
图片预览







文档简介
课件22张PPT。2、3不等式的解集 观察下面的式子,回答什么叫不等式?(用不等号表示不等关系的式子叫不等式)观察思考 由“等式表示相等关系”,我们会想到:在现实生活中,同种量之间有没有不等关系呢?(如身高与身高、面积与面积等)请你们举一些实例。 www.ulaik.cn
1、判断下列式子哪些是不等式
(1)3> 2
(2) a2+1> 0
(3) 3 x 2+2 x
(4) x< 2 x +1
(5) x =2 x -5
(6) x 2+4 x < 3 x +1
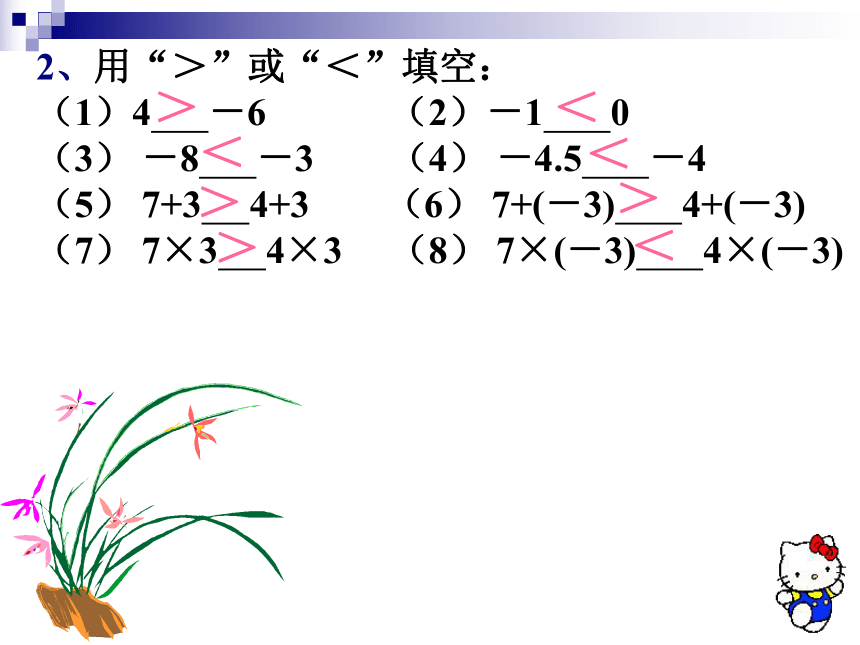
(7) a+b≠c√√√√√>>>><<<<2、用“>”或“<”填空:
(1)4 -6 (2)-1 0
(3) -8 -3 (4) -4.5 -4
(5) 7+3 4+3 (6) 7+(-3) 4+(-3)
(7) 7×3 4×3 (8) 7×(-3) 4×(-3)回忆思考★表示相等关系的式子叫等式。
★等号左边的代数式叫等式的左边;
★等号右边的代数式叫等式的右边。2、观察下面这几个式子,完成下面的填空。回忆思考同一个数同一个整式等式的基本性质1:3、继续观察下面这几个式子,完成下面的填空。回忆思考同一个数等式的基本性质2: 从上面的回忆可知,等式有两条基本性质,那么不等式有没有类似的性质呢?
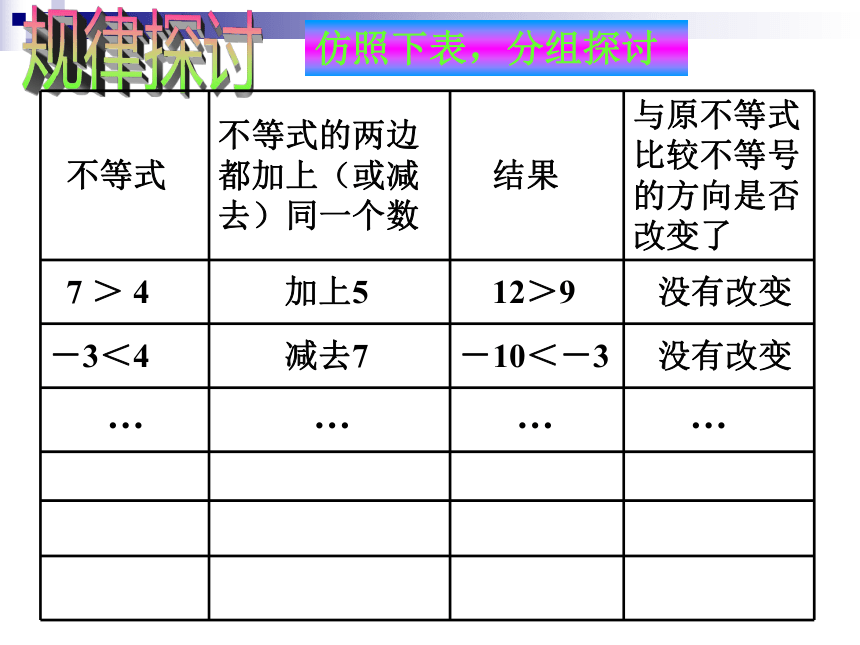
回答是肯定的,有。我们今天的主要任务就是研究不等式有哪些性质?规律探讨仿照下表,分组探讨不等式的性质1: 不等式的两边都加上(或减去)同一个数,不等号的方向不变。由上面的探讨我们可以得出:这个性质可以用数学语言表示为:<>规律探讨仿照下表,分组探讨不等式的基本性质 2: 不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。由上面的探讨我们可以继续得出:这个性质可以用数学语言表示为:1、如果x+5>4,那么两边都 可得 x >-1
2、在-7<8 的两边都加上9可得 。
3、在5>-2 的两边都减去6可得 。
4、在-3>-4 的两边都乘以7可得 。
5、在-8<0 的两边都除以8 可得 。 减去52<17-1>-8-21>-28-1<0规律探讨仿照下表,分组探讨不等式的基本性质 3: 不等式的两边都乘以(或除以)同一个负数,不等号的方向要改变。由上面的探讨我们可以继续得出:这个性质可以用数学语言表示为:1>09<12>>><1231 这种解法对吗?如果正确,说出它根据的是不等式的哪一条基本性质;如果不正确,请就明理由。解 (1)根据不等式的性质1,两边都加上2得:
x-2+2<3+2
即 x <5
(2)根据不等式的性质1,两边都减去5 x 得:
6 x -5 x <(5 x -1)-5 x
即 x <-1③④ 同学回答不等式的三条性质是:
① 、不等式的两边都加上(或减去)同一个 数或同一个整式,不等号的方向不变;
② 、不等式的两边都乘以(或除以)同一个 正数,不等号的方向不变;
③ 、*不等式的两边都乘以(或除以)同一个负数,不等号的方向要改变 ;小结一本节重点(1)掌握不等式的三条性质,尤其是性质3;
(2)能正确应用性质对不等式进行变形;小结二
当不等式两边都乘以(或除以)同 一个数时,一定要看清是正数还是负数;对于未给定范围的字母,应分情况讨论。注意事项作业: 完成教材和练习册中的练习题。
1、判断下列式子哪些是不等式
(1)3> 2
(2) a2+1> 0
(3) 3 x 2+2 x
(4) x< 2 x +1
(5) x =2 x -5
(6) x 2+4 x < 3 x +1
(7) a+b≠c√√√√√>>>><<<<2、用“>”或“<”填空:
(1)4 -6 (2)-1 0
(3) -8 -3 (4) -4.5 -4
(5) 7+3 4+3 (6) 7+(-3) 4+(-3)
(7) 7×3 4×3 (8) 7×(-3) 4×(-3)回忆思考★表示相等关系的式子叫等式。
★等号左边的代数式叫等式的左边;
★等号右边的代数式叫等式的右边。2、观察下面这几个式子,完成下面的填空。回忆思考同一个数同一个整式等式的基本性质1:3、继续观察下面这几个式子,完成下面的填空。回忆思考同一个数等式的基本性质2: 从上面的回忆可知,等式有两条基本性质,那么不等式有没有类似的性质呢?
回答是肯定的,有。我们今天的主要任务就是研究不等式有哪些性质?规律探讨仿照下表,分组探讨不等式的性质1: 不等式的两边都加上(或减去)同一个数,不等号的方向不变。由上面的探讨我们可以得出:这个性质可以用数学语言表示为:<>规律探讨仿照下表,分组探讨不等式的基本性质 2: 不等式的两边都乘以(或除以)同一个正数,不等号的方向不变。由上面的探讨我们可以继续得出:这个性质可以用数学语言表示为:1、如果x+5>4,那么两边都 可得 x >-1
2、在-7<8 的两边都加上9可得 。
3、在5>-2 的两边都减去6可得 。
4、在-3>-4 的两边都乘以7可得 。
5、在-8<0 的两边都除以8 可得 。 减去52<17-1>-8-21>-28-1<0规律探讨仿照下表,分组探讨不等式的基本性质 3: 不等式的两边都乘以(或除以)同一个负数,不等号的方向要改变。由上面的探讨我们可以继续得出:这个性质可以用数学语言表示为:1>09<12>>><1231 这种解法对吗?如果正确,说出它根据的是不等式的哪一条基本性质;如果不正确,请就明理由。解 (1)根据不等式的性质1,两边都加上2得:
x-2+2<3+2
即 x <5
(2)根据不等式的性质1,两边都减去5 x 得:
6 x -5 x <(5 x -1)-5 x
即 x <-1③④ 同学回答不等式的三条性质是:
① 、不等式的两边都加上(或减去)同一个 数或同一个整式,不等号的方向不变;
② 、不等式的两边都乘以(或除以)同一个 正数,不等号的方向不变;
③ 、*不等式的两边都乘以(或除以)同一个负数,不等号的方向要改变 ;小结一本节重点(1)掌握不等式的三条性质,尤其是性质3;
(2)能正确应用性质对不等式进行变形;小结二
当不等式两边都乘以(或除以)同 一个数时,一定要看清是正数还是负数;对于未给定范围的字母,应分情况讨论。注意事项作业: 完成教材和练习册中的练习题。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
