第二章 随机变量及其分布 单元测试卷A(含答案解析)
文档属性
| 名称 | 第二章 随机变量及其分布 单元测试卷A(含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-21 16:05:48 | ||
图片预览




文档简介
随机变量及其分布单元测试卷(A)
一、单选题
1.随机变量的分布列如下,且满足,则的值( )
1 2 3
A.0 B.1
C.2 D.无法确定,与,有关
2.已知随机变量,若,则,分别是( )
A.4和2.4 B.2和2.4 C.6和2.4 D.4和5.6
3.已知随机变量的分布,则 ( )
-1 0 1
A.0 B.-0.2 C.-1 D.-0.3
4.已知是离散型随机变量,,,,则( )
A. B. C. D.
5.设随机变量,若,则( )
A. B. C. D.
6.设,则随机变量的分布列是:
则当在内增大时( )
A.增大 B.减小
C.先增大后减小 D.先减小后增大
7.设~,,,则的值分别为( )
A. B. C. D.
8.在篮球比赛中,罚球命中次得分,不中得分.如果运动员甲罚球命中的概率是,记运动员甲罚球次的得分为,则等于( ).
A. B. C. D.
9.已知随机变量和,其中,且,若的分布列如下表,则的值为( )
ξ 1 2 3 4
P m n
A. B. C. D.
10.已知Y=5X+1,E(Y)=6,则E(X)的值为( )
A.6 B.5
C.1 D.7
11.同时抛掷两枚均匀的硬币10次,设两枚硬币同时出现反面的次数为ξ,则D(ξ)=( )
A. B.
C. D.5
12.随机变量ξ的分布列如下表,且E(ξ)=1.1,则D(ξ)=( )
ξ 0 1 x
P p
A.0.36 B.0.52
C.0.49 D.0.68
二、填空题
13.抛掷两个骰子,至少有一个4点或5点出现时,就说这次试验成功,则在10次试验中,成功次数的期望是______.
14.100件产品中有5件次品,不放回地抽取2次,每次抽1件.已知第1次抽出的是次品,则第2次抽出正品的概率是_________.
15.随机变量X的分布列是
1 2 3
P 0.4 0.2 0.4
则EX,DX分别是________
16.有10道数学单项选择题,每题选对得4分,不选或选错得0分.已知某考生能正确答对其中的7道题,余下的3道题每题能正确答对的概率为.假设每题答对与否相互独立,记为该考生答对的题数,为该考生的得分,则__________,__________(用数字作答).
17.小张同学拿到一个随机变量的概率分布列如下表,然后要计算的数学期望.尽管“!”处完全无法看清,且两个“?”处字迹模糊,但能判定这两个“?”处的数值相同.据此,小张给出了正确答案__________.
2 4 6
? ! ?
三、解答题
18.为调查某公司五类机器的销售情况,该公司随机收集了一个月销售的有关数据,公司规定同一类机器销售价格相同,经分类整理得到下表:
机器类型 第一类 第二类 第三类 第四类 第五类
销售总额(万元)
销售量(台)
利润率
利润率是指:一台机器销售价格减去出厂价格得到的利润与该机器销售价格的比值.
(Ⅰ)从该公司本月卖出的机器中随机选一台,求这台机器利润率高于0.2的概率;
(Ⅱ)从该公司本月卖出的销售单价为20万元的机器中随机选取台,求这两台机器的利润率不同的概率;
(Ⅲ)假设每类机器利润率不变,销售一台第一类机器获利万元,销售一台第二类机器获利万元,…,销售一台第五类机器获利,依据上表统计数据,随机销售一台机器获利的期望为,设,试判断与的大小.(结论不要求证明)
19.设袋子中装有个红球,个黄球,个篮球,且规定:取出一个红球得1分,取出一个黄球得2分,取出一个篮球得3分.
(Ⅰ)当,,时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量为取出此2球所得分数之和,求的分布列;
(Ⅱ)从该袋中任取(每球取到的机会均等)1个球,记随机变量为取出此球所得分数.若,,求.
20.某校高二年级组织成语听说大赛,每班选10名同学参赛,要求每位同学回答5个成语,各位同学的得分总和算作本班成绩,其中一班的张明同学参赛,他每道题答对的概率均为,且每道题答对与否互不影响.计分办法规定为答对不超过3个题时,每答对一个得一分,超过三个,每多答对一个得两分.
(1)求张明至少答对三道题的概率;
(2)设张明答完5道题得分为,求的分布列及数学期望.
21.袋中有20个大小相同的球,其中标有号码0的球有10个,标有号码的球有个,其中1,2,3,4.现从袋中任取1球,表示所取球的号码.
(1)求的分布列、均值和方差;
(2)若,且,,求,的值.
22.根据以往的经验,某建筑工程施工期间的降水量(单位:)对工期的影响如下表:
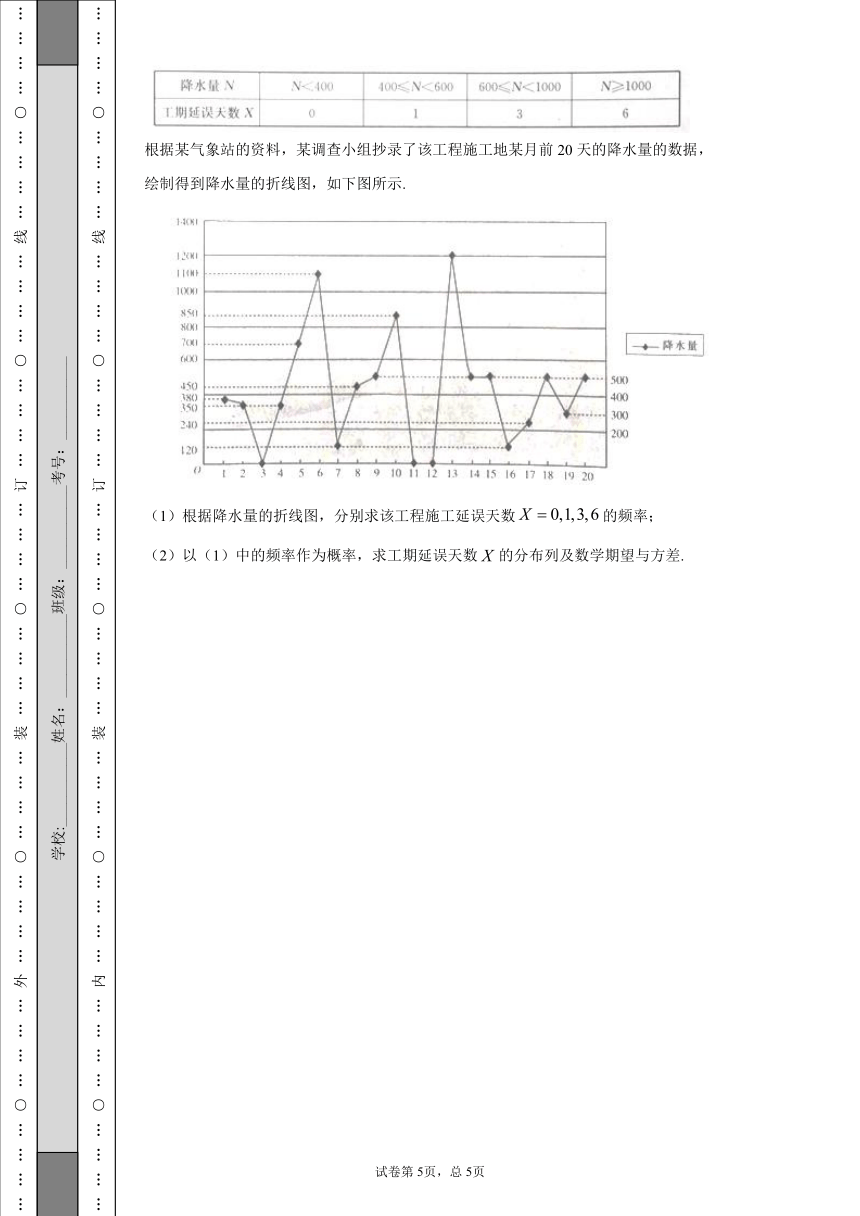
根据某气象站的资料,某调查小组抄录了该工程施工地某月前20天的降水量的数据,绘制得到降水量的折线图,如下图所示.
(1)根据降水量的折线图,分别求该工程施工延误天数的频率;
(2)以(1)中的频率作为概率,求工期延误天数的分布列及数学期望与方差.
参考答案
1.B【解析】
由随机变量的分布列得到:,
又,解得,∴,∴.故选:B.
2.A【解析】
故选A.
3.B【解析】,
,
根据随机变量期望公式,
得,故选B.
4.A【解析】是离散型随机变量,,,,
由已知得,
解得,
,
.故选:A.
5.C【解析】根据正态分布曲线关于x=3对称,所以P(X>4)=P(X<2)=p,所以P(2<X<4)=1-2p,故选C.
6.D【解析】由分布列得,则
,则当在内增大时,先减小后增大.
7.D【解析】
依题意得,解得.
8.C【解析】
由题意得的取值范围为,,,
所以.故选.
9.A【解析】且,则
即
解得 故答案选A
10.C【解析】因为E(Y)=E(5X+1)=5E(X)+1=6,所以E(X)=1.
11.A【解析】
两枚同时出现反面的概率为,所以为次独立重复试验,属于二项分布,方差为.
12.C【解析】根据,由,故.
13.【解析】
在一次试验中成功的概率为1-×=,
∵X~B,∴E(X)=np=10×=.
14.【解析】在第次抽到次品后,还有有件次品,件正品,
则第二次抽到正品的概率为,故答案为.
15.2,0.8
【解析】Eξ=1×0.4+2×0.2+3×0.4=2,
Dξ=(1﹣2)2×0.4+(2﹣2)2×0.2+(3﹣2)2×0.4=0.8.
故答案为:2,0.8.
16.
【解析】(1).
(2)由题意可得:,
,,
,,
的分布列为:
..故答案为,32.
17.4【解析】设“?”为x,“!”为y,由离散型的随机变量的分布列的性质可得2x+y=1.
∴Eξ=2×x+4y+6x=4(2x+y)=4.故答案为:4
18.(Ⅰ)(Ⅱ)(Ⅲ)
【解析】(Ⅰ)由题意知,本月共卖出30台机器,
利润率高于0.2的是第一类和第四类,共有10台.
设“这台机器利润率高于0.2”为事件,
则.
(Ⅱ)用销售总额除以销售量得到机器的销售单价,可知第一类与第三类的机器销售单价为20万,
第一类有台,第三类有台,共有台,随机选取台有种不同方法,
两台机器的利润率不同则每类各取一台有种不同方法,
设两台机器的利润率不同为事件,则.
(Ⅲ)由题意可得,可能取的值为
,,,,
因此;
又,
所以.
19.(Ⅰ)详见解析;(Ⅱ).
【解析】(Ⅰ)由题意得取2,3,4,5,6.
故,,,
,.
所以的分布列为
2 3 4 5 6
(Ⅱ)由题意知的分布列为
1 2 3
所以
,
.
解得 ,,故
20.(1)(2)见解析
【解析】(1)设“张明至少答对三道题”为事件,
则
(2)由条件可知的可能取值为0,1,2,3,5,7
,
,
,
,
,
.
所以的分布列为
故数学期望
21.(1)见解析;(2)或
【解析】(1)可能取值有,
,,,
,,
∴ 的分布列为
∴ ;
(2)∵ ,
∴ ,
∴ 或.
22.【解析】(1)∵的天数为10,∴的频率为.
∵的天数为6,∴的频率为.
∵的天数为2,∴的频率为.
(2)的分布列为
.
.
试卷第1页,总3页
试卷第1页,总3页
