2020年春季人教版数学七年级下册5.1相交线同步练习含解析
文档属性
| 名称 | 2020年春季人教版数学七年级下册5.1相交线同步练习含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 787.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-21 00:00:00 | ||
图片预览




文档简介
相交线
1. (2019·黑龙江初一期中)下列各图中,∠1与∠2是对顶角的是( )
A. B. C. D.
2. (2020·四川初一期末)如图,,,点,,在同一直线上,则的度数
为
A. B. C. D.
3. (2019·重庆市綦江区城南中学初一期末)图中∠1的对顶角是( )
A.∠2 B.∠3 C.∠4 D.∠5
4. (2019·深圳市光明区实验学校初一期末)如图,CO⊥AB,垂足为O,∠DOE=90°,下列结论不正确的是( )
A.∠1+∠2=90° B.∠2+∠3=90° C.∠1+∠3=90° D.∠3+∠4=90°
5. (2019·河北初一期末)点是直线外一点,、、为直线上的三点,,,,则点到直线的距离( )
A.小于 B.等于 C.不大于 D.等于
6. (2019·云南初一月考)如图,直线b、c被直线a所截,则∠1与∠2是( )
A.同位角 B.内错角 C.同旁内角 D.对顶角
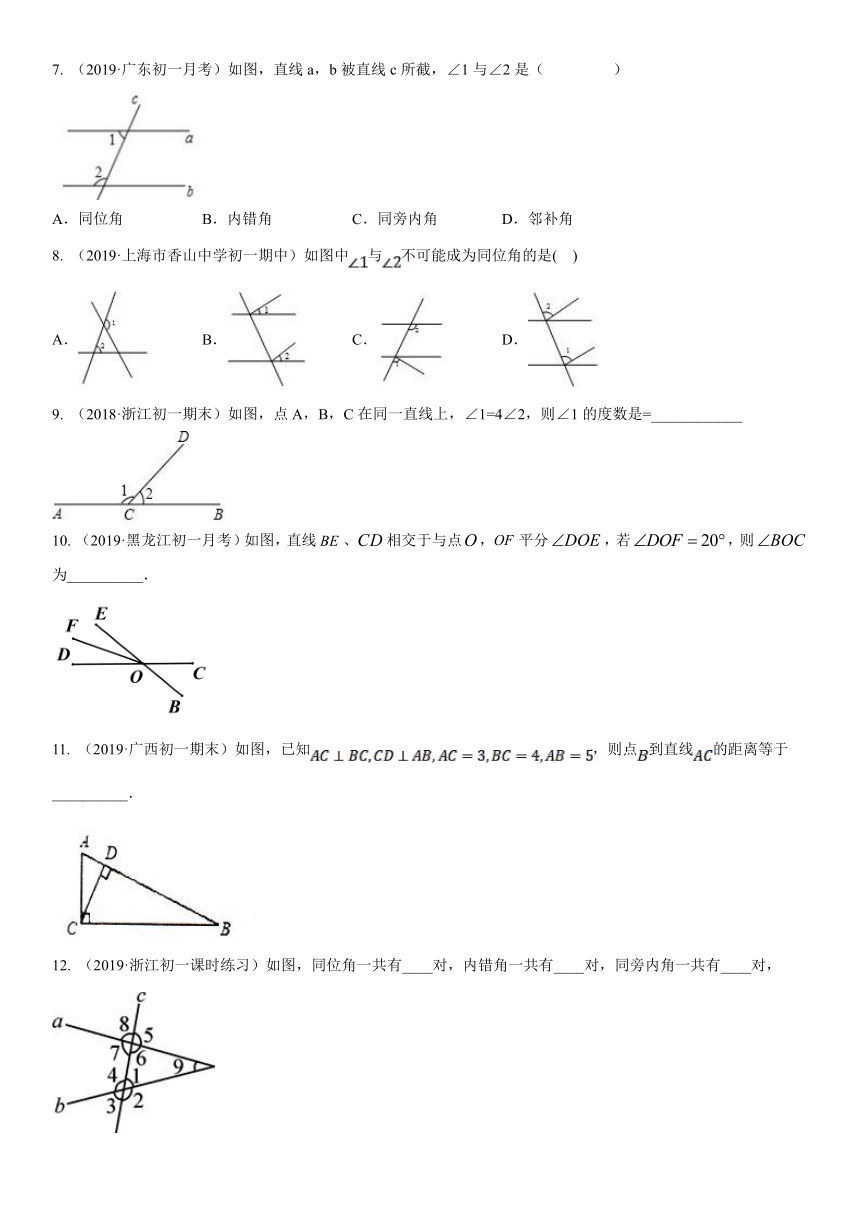
7. (2019·广东初一月考)如图,直线a,b被直线c所截,∠1与∠2是( )
A.同位角 B.内错角 C.同旁内角 D.邻补角
8. (2019·上海市香山中学初一期中)如图中与不可能成为同位角的是(????)
A. B. C. D.
9. (2018·浙江初一期末)如图,点A,B,C在同一直线上,∠1=4∠2,则∠1的度数是=____________
10. (2019·黑龙江初一月考)如图,直线、相交于与点,平分,若,则为__________.
11. (2019·广西初一期末)如图,已知,则点到直线的距离等于__________.
12. (2019·浙江初一课时练习)如图,同位角一共有____对,内错角一共有____对,同旁内角一共有____对,
13.如图,直线AB,CD与EF相交.
(1)图中∠1和∠2分别在直线AB,CD的同_______,并且都在直线EF的_____,具有这样位置关系的一对角叫做______;
(2)图中∠2和∠8都在直线AB,CD____,并且分别在直线EF的___,具有这样位置关系的一对角叫做_____;
(3)图中∠2和∠7都在直线AB,CD____,且都在直线EF的____,具有这样位置关系的一对角叫做______.
14. (2020·江苏初一期末)如图,直线AB、CD相交于点O,已知∠AOC=75°,∠BOE :∠DOE=2:3.
(1)求∠BOE的度数;
(2)若OF平分∠AOE,∠AOC与∠AOF相等吗?为什么?
15. 如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
16. (2018·贵州初一期中)如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系,并说明理由;
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
答案
1. (2019·黑龙江初一期中)下列各图中,∠1与∠2是对顶角的是( )
A. B. C. D.
【答案】C
【解析】
解:∵互为对顶角的两个角的两边互为反向延长线,
∴A中∠1和∠2是邻补角,C中的∠1和∠2是对顶角.
故选:C.
【点睛】
本题主要考查的是邻补角、对顶角的定义,熟练掌握相关概念是解题的关键.
2. (2020·四川初一期末)如图,,,点,,在同一直线上,则的度数
为
A. B. C. D.
【答案】C
【解析】
∵AOC= ∠1 =15
∴∠BOC=75
又 ∵B、O、D在同一直线上,即∠BOD=180
∴∠BOC=∠BOD-∠BOC=180-75=105°
3. (2019·重庆市綦江区城南中学初一期末)图中∠1的对顶角是( )
A.∠2 B.∠3 C.∠4 D.∠5
【答案】B
【解析】
由图形可知,∠1的对顶角是∠3,
故选B.
【点睛】
本题考查了对顶角的识别,熟练掌握对顶角的图形特征是解题的关键.
4. (2019·深圳市光明区实验学校初一期末)如图,CO⊥AB,垂足为O,∠DOE=90°,下列结论不正确的是( )
A.∠1+∠2=90° B.∠2+∠3=90° C.∠1+∠3=90° D.∠3+∠4=90°
【答案】C
【解析】
解:如图,∵CO⊥AB,
∴∠BOC=∠1+∠2=∠3+∠4=90°,
∵∠DOE=90°,
∴∠2+∠3=90°,
∴∠1+∠4=90°,
∴结论不正确的是:∠1+∠3=90°,
故选:C.
【点睛】
本题考查了垂线.要注意领会由垂直得直角这一要点.
5. (2019·河北初一期末)点是直线外一点,、、为直线上的三点,,,,则点到直线的距离( )
A.小于 B.等于 C.不大于 D.等于
【答案】C
【解析】
解:点P为直线l外一点,当P点直线l上的三点A、B、C的距离分别为PA=4cm,PB=5cm,PC=2cm,则点P到直线l的距离为不大于2cm,
故选:C.
【点睛】
本题考查了点到直线的距离,点到直线的距离是点到直线的垂线段的长度,利用垂线段最短是解题关键.
6. (2019·云南初一月考)如图,直线b、c被直线a所截,则∠1与∠2是( )
A.同位角 B.内错角 C.同旁内角 D.对顶角
【答案】A
【解析】
直线b,c被直线a所截,∠1与∠2在直线a的同侧,
则∠1与∠2是同位角。
故选:A.
7. (2019·广东初一月考)如图,直线a,b被直线c所截,∠1与∠2是( )
A.同位角 B.内错角 C.同旁内角 D.邻补角
【答案】C
【解析】
解:直线a,b被直线c所截,∠1与∠2是同旁内角,
故选:C.
【点睛】
本题考查了同位角、内错角、同旁内角的定义,能熟记同位角、内错角、同旁内角的定义的内容是解此题的关键,注意数形结合.
8. (2019·上海市香山中学初一期中)如图中与不可能成为同位角的是(????)
A. B. C. D.
【答案】B
【解析】
解:根据同位角的定义观察图形,选项B中∠1与∠2不可能成为同位角.故答案为B.
【点睛】
本题考查了同位角的定义,熟练掌握定义是解题的关键.
9. (2018·浙江初一期末)如图,点A,B,C在同一直线上,∠1=4∠2,则∠1的度数是=____________
【答案】144°.
【解析】
∵点A,B,C在同一直线上,∠1=4∠2,
∴∠1+∠2=∠1+∠1=180°,
解得:∠1=144°,
故答案为:144°.
【点睛】
本题主要考查的是邻补角的定义,依据题意列出方程是解题的关键.
10. (2019·黑龙江初一月考)如图,直线、相交于与点,平分,若,则为__________.
【答案】40°
【解析】
∵∠BOC=20°,平分,
∴∠DOE=2∠BOC=40°,
∵∠DOE和∠BOC是对顶角,
∴∠BOC=∠DOE=40°,
故答案为:40°.
【点睛】
考核知识点:对顶角性质.理解对顶角性质是关键.
11. (2019·广西初一期末)如图,已知,则点到直线的距离等于__________.
【答案】4
【解析】
解:根据垂线段、点到直线距离的定义可知,
点B到直线AC的距离等于BC的长度,
即为4.
【点睛】
本题考查了点到直线的距离,利用点到直线的距离是直线外的点到直线的垂线段的长度是解题关键.
12. (2019·浙江初一课时练习)如图,同位角一共有____对,内错角一共有____对,同旁内角一共有____对,
【答案】6, 4, 4.
【解析】
解:同位角一共有6对,分别是∠1和∠5,∠2和∠6,∠3和∠7,∠4和∠8,∠7和∠9,∠4和∠9;内错角一共有4对,分别是∠1和∠7,∠4和∠6,∠5和∠9,∠2和∠9;同旁内角一共有4对,分别是∠1和∠6,∠1和∠9,∠4和∠7,∠6和∠9.
故答案为:6;4;4.
【点睛】
本题考查同位角,内错角,以及同旁内角,熟练掌握各自的定义是解题关键
13. (2019·全国初一课时练习)如图,直线AB,CD与EF相交.
(1)图中∠1和∠2分别在直线AB,CD的同_______,并且都在直线EF的_____,具有这样位置关系的一对角叫做______;
(2)图中∠2和∠8都在直线AB,CD____,并且分别在直线EF的___,具有这样位置关系的一对角叫做_____;
(3)图中∠2和∠7都在直线AB,CD____,且都在直线EF的____,具有这样位置关系的一对角叫做______.
【答案】(1) 同一方(或上方),同侧(或右侧),同位角;(2)之间,两侧,内错角;(3)之间,同一旁(或右侧),同旁内角.
【解析】
(1)同位角:两条直线被第三条直线所截,在截线的同旁,被截两直线的同一侧的角,我们把这样的两个角称为同位角。
(2)内错角:两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角。
(3)同旁内角:两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内角。同旁内角,“同旁”指在第三条直线的同侧;“内”指在被截两条直线之间
故答案为:(1) 同一方(或上方),同侧(或右侧),同位角;(2)之间,两侧,内错角;(3)之间,同一旁(或右侧),同旁内角.
14. (2020·江苏初一期末)如图,直线AB、CD相交于点O,已知∠AOC=75°,∠BOE :∠DOE=2:3.
(1)求∠BOE的度数;
(2)若OF平分∠AOE,∠AOC与∠AOF相等吗?为什么?
【答案】(1)30°;(2)相等,理由见解析
【解析】
(1)设∠BOE=2x,则∠EOD=3x,
∠BOD=∠AOC=75°,
∴2x+3x=75°,
解得,x=15°,
则2x=30°,3x=45°,
∴∠BOE=30°;
(2)∵∠BOE=30°,
∴∠AOE=150°,
∵OF平分∠AOE,
∴∠AOF=75°,
∴∠AOF=∠AOC,
【点睛】
本题考查的是对顶角、邻补角的概念和性质、角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.
15. (2020·全国初三专题练习)如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
【答案】(1)55°(2)①x②100°
【解析】
解:(1)由对顶角相等可知:∠BOD=∠AOC=70°,
∵∠FOB=∠DOF-∠BOD,
∴∠FOB=90°-70°=20°,
∵OE平分∠BOD,
∴∠BOE=∠BOD=×70°=35°,
∴∠EOF=∠FOB+∠BOE=35°+20°=55°;
(2)①∵OE平分∠BOD,
∴∠BOE=∠DOE,
∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,
∴∠COE=∠AOE=x°,
∵OF平分∠COE,
∴∠EOF=x°;
②∵∠BOE=∠FOE-∠FOB,
∴∠BOE=x°-15°,
∵∠BOE+∠AOE=180°,
∴x°-15°+x°=180°,解得:x=130,
∴∠AOC=2∠BOE=2×(180°-130°)=100°.
【点睛】
本题考查对顶角,邻补角以及角平分线定义,主要考查学生的计算能力,熟练掌握角平分线的定义是解题的关键.
16. (2018·贵州初一期中)如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系,并说明理由;
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
【答案】(1) OF⊥OD,理由见解析;(2) 60°.
【解析】
(1)因为OF平分∠AOE,
所以∠AOF=∠EOF=∠AOE.
又因为∠DOE=∠BOD=∠BOE,
所以∠DOE+∠EOF=(∠BOE+∠AOE)= ×180°=90°,
即∠FOD=90°.
所以OF⊥OD.
(2)设∠AOC=x°,
因为∠AOC∶∠AOD=1∶5,
所以∠AOD=5x°.
因为∠AOC+∠AOD=180°,
所以x+5x=180,x=30.
所以∠DOE=∠BOD=∠AOC=30°.
又因为∠FOD=90°,
所以∠EOF=90°-30°=60°.
1. (2019·黑龙江初一期中)下列各图中,∠1与∠2是对顶角的是( )
A. B. C. D.
2. (2020·四川初一期末)如图,,,点,,在同一直线上,则的度数
为
A. B. C. D.
3. (2019·重庆市綦江区城南中学初一期末)图中∠1的对顶角是( )
A.∠2 B.∠3 C.∠4 D.∠5
4. (2019·深圳市光明区实验学校初一期末)如图,CO⊥AB,垂足为O,∠DOE=90°,下列结论不正确的是( )
A.∠1+∠2=90° B.∠2+∠3=90° C.∠1+∠3=90° D.∠3+∠4=90°
5. (2019·河北初一期末)点是直线外一点,、、为直线上的三点,,,,则点到直线的距离( )
A.小于 B.等于 C.不大于 D.等于
6. (2019·云南初一月考)如图,直线b、c被直线a所截,则∠1与∠2是( )
A.同位角 B.内错角 C.同旁内角 D.对顶角
7. (2019·广东初一月考)如图,直线a,b被直线c所截,∠1与∠2是( )
A.同位角 B.内错角 C.同旁内角 D.邻补角
8. (2019·上海市香山中学初一期中)如图中与不可能成为同位角的是(????)
A. B. C. D.
9. (2018·浙江初一期末)如图,点A,B,C在同一直线上,∠1=4∠2,则∠1的度数是=____________
10. (2019·黑龙江初一月考)如图,直线、相交于与点,平分,若,则为__________.
11. (2019·广西初一期末)如图,已知,则点到直线的距离等于__________.
12. (2019·浙江初一课时练习)如图,同位角一共有____对,内错角一共有____对,同旁内角一共有____对,
13.如图,直线AB,CD与EF相交.
(1)图中∠1和∠2分别在直线AB,CD的同_______,并且都在直线EF的_____,具有这样位置关系的一对角叫做______;
(2)图中∠2和∠8都在直线AB,CD____,并且分别在直线EF的___,具有这样位置关系的一对角叫做_____;
(3)图中∠2和∠7都在直线AB,CD____,且都在直线EF的____,具有这样位置关系的一对角叫做______.
14. (2020·江苏初一期末)如图,直线AB、CD相交于点O,已知∠AOC=75°,∠BOE :∠DOE=2:3.
(1)求∠BOE的度数;
(2)若OF平分∠AOE,∠AOC与∠AOF相等吗?为什么?
15. 如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
16. (2018·贵州初一期中)如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系,并说明理由;
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
答案
1. (2019·黑龙江初一期中)下列各图中,∠1与∠2是对顶角的是( )
A. B. C. D.
【答案】C
【解析】
解:∵互为对顶角的两个角的两边互为反向延长线,
∴A中∠1和∠2是邻补角,C中的∠1和∠2是对顶角.
故选:C.
【点睛】
本题主要考查的是邻补角、对顶角的定义,熟练掌握相关概念是解题的关键.
2. (2020·四川初一期末)如图,,,点,,在同一直线上,则的度数
为
A. B. C. D.
【答案】C
【解析】
∵AOC= ∠1 =15
∴∠BOC=75
又 ∵B、O、D在同一直线上,即∠BOD=180
∴∠BOC=∠BOD-∠BOC=180-75=105°
3. (2019·重庆市綦江区城南中学初一期末)图中∠1的对顶角是( )
A.∠2 B.∠3 C.∠4 D.∠5
【答案】B
【解析】
由图形可知,∠1的对顶角是∠3,
故选B.
【点睛】
本题考查了对顶角的识别,熟练掌握对顶角的图形特征是解题的关键.
4. (2019·深圳市光明区实验学校初一期末)如图,CO⊥AB,垂足为O,∠DOE=90°,下列结论不正确的是( )
A.∠1+∠2=90° B.∠2+∠3=90° C.∠1+∠3=90° D.∠3+∠4=90°
【答案】C
【解析】
解:如图,∵CO⊥AB,
∴∠BOC=∠1+∠2=∠3+∠4=90°,
∵∠DOE=90°,
∴∠2+∠3=90°,
∴∠1+∠4=90°,
∴结论不正确的是:∠1+∠3=90°,
故选:C.
【点睛】
本题考查了垂线.要注意领会由垂直得直角这一要点.
5. (2019·河北初一期末)点是直线外一点,、、为直线上的三点,,,,则点到直线的距离( )
A.小于 B.等于 C.不大于 D.等于
【答案】C
【解析】
解:点P为直线l外一点,当P点直线l上的三点A、B、C的距离分别为PA=4cm,PB=5cm,PC=2cm,则点P到直线l的距离为不大于2cm,
故选:C.
【点睛】
本题考查了点到直线的距离,点到直线的距离是点到直线的垂线段的长度,利用垂线段最短是解题关键.
6. (2019·云南初一月考)如图,直线b、c被直线a所截,则∠1与∠2是( )
A.同位角 B.内错角 C.同旁内角 D.对顶角
【答案】A
【解析】
直线b,c被直线a所截,∠1与∠2在直线a的同侧,
则∠1与∠2是同位角。
故选:A.
7. (2019·广东初一月考)如图,直线a,b被直线c所截,∠1与∠2是( )
A.同位角 B.内错角 C.同旁内角 D.邻补角
【答案】C
【解析】
解:直线a,b被直线c所截,∠1与∠2是同旁内角,
故选:C.
【点睛】
本题考查了同位角、内错角、同旁内角的定义,能熟记同位角、内错角、同旁内角的定义的内容是解此题的关键,注意数形结合.
8. (2019·上海市香山中学初一期中)如图中与不可能成为同位角的是(????)
A. B. C. D.
【答案】B
【解析】
解:根据同位角的定义观察图形,选项B中∠1与∠2不可能成为同位角.故答案为B.
【点睛】
本题考查了同位角的定义,熟练掌握定义是解题的关键.
9. (2018·浙江初一期末)如图,点A,B,C在同一直线上,∠1=4∠2,则∠1的度数是=____________
【答案】144°.
【解析】
∵点A,B,C在同一直线上,∠1=4∠2,
∴∠1+∠2=∠1+∠1=180°,
解得:∠1=144°,
故答案为:144°.
【点睛】
本题主要考查的是邻补角的定义,依据题意列出方程是解题的关键.
10. (2019·黑龙江初一月考)如图,直线、相交于与点,平分,若,则为__________.
【答案】40°
【解析】
∵∠BOC=20°,平分,
∴∠DOE=2∠BOC=40°,
∵∠DOE和∠BOC是对顶角,
∴∠BOC=∠DOE=40°,
故答案为:40°.
【点睛】
考核知识点:对顶角性质.理解对顶角性质是关键.
11. (2019·广西初一期末)如图,已知,则点到直线的距离等于__________.
【答案】4
【解析】
解:根据垂线段、点到直线距离的定义可知,
点B到直线AC的距离等于BC的长度,
即为4.
【点睛】
本题考查了点到直线的距离,利用点到直线的距离是直线外的点到直线的垂线段的长度是解题关键.
12. (2019·浙江初一课时练习)如图,同位角一共有____对,内错角一共有____对,同旁内角一共有____对,
【答案】6, 4, 4.
【解析】
解:同位角一共有6对,分别是∠1和∠5,∠2和∠6,∠3和∠7,∠4和∠8,∠7和∠9,∠4和∠9;内错角一共有4对,分别是∠1和∠7,∠4和∠6,∠5和∠9,∠2和∠9;同旁内角一共有4对,分别是∠1和∠6,∠1和∠9,∠4和∠7,∠6和∠9.
故答案为:6;4;4.
【点睛】
本题考查同位角,内错角,以及同旁内角,熟练掌握各自的定义是解题关键
13. (2019·全国初一课时练习)如图,直线AB,CD与EF相交.
(1)图中∠1和∠2分别在直线AB,CD的同_______,并且都在直线EF的_____,具有这样位置关系的一对角叫做______;
(2)图中∠2和∠8都在直线AB,CD____,并且分别在直线EF的___,具有这样位置关系的一对角叫做_____;
(3)图中∠2和∠7都在直线AB,CD____,且都在直线EF的____,具有这样位置关系的一对角叫做______.
【答案】(1) 同一方(或上方),同侧(或右侧),同位角;(2)之间,两侧,内错角;(3)之间,同一旁(或右侧),同旁内角.
【解析】
(1)同位角:两条直线被第三条直线所截,在截线的同旁,被截两直线的同一侧的角,我们把这样的两个角称为同位角。
(2)内错角:两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角。
(3)同旁内角:两条直线被第三条直线所截,在截线同旁,且在被截线之内的两角,叫做同旁内角。同旁内角,“同旁”指在第三条直线的同侧;“内”指在被截两条直线之间
故答案为:(1) 同一方(或上方),同侧(或右侧),同位角;(2)之间,两侧,内错角;(3)之间,同一旁(或右侧),同旁内角.
14. (2020·江苏初一期末)如图,直线AB、CD相交于点O,已知∠AOC=75°,∠BOE :∠DOE=2:3.
(1)求∠BOE的度数;
(2)若OF平分∠AOE,∠AOC与∠AOF相等吗?为什么?
【答案】(1)30°;(2)相等,理由见解析
【解析】
(1)设∠BOE=2x,则∠EOD=3x,
∠BOD=∠AOC=75°,
∴2x+3x=75°,
解得,x=15°,
则2x=30°,3x=45°,
∴∠BOE=30°;
(2)∵∠BOE=30°,
∴∠AOE=150°,
∵OF平分∠AOE,
∴∠AOF=75°,
∴∠AOF=∠AOC,
【点睛】
本题考查的是对顶角、邻补角的概念和性质、角平分线的定义,掌握对顶角相等、邻补角之和等于180°是解题的关键.
15. (2020·全国初三专题练习)如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=70°,∠DOF=90°,求∠EOF的度数;
(2)若OF平分∠COE,∠BOF=15°,若设∠AOE=x°.
①用含x的代数式表示∠EOF;
②求∠AOC的度数.
【答案】(1)55°(2)①x②100°
【解析】
解:(1)由对顶角相等可知:∠BOD=∠AOC=70°,
∵∠FOB=∠DOF-∠BOD,
∴∠FOB=90°-70°=20°,
∵OE平分∠BOD,
∴∠BOE=∠BOD=×70°=35°,
∴∠EOF=∠FOB+∠BOE=35°+20°=55°;
(2)①∵OE平分∠BOD,
∴∠BOE=∠DOE,
∵∠BOE+∠AOE=180°,∠COE+∠DOE=180°,
∴∠COE=∠AOE=x°,
∵OF平分∠COE,
∴∠EOF=x°;
②∵∠BOE=∠FOE-∠FOB,
∴∠BOE=x°-15°,
∵∠BOE+∠AOE=180°,
∴x°-15°+x°=180°,解得:x=130,
∴∠AOC=2∠BOE=2×(180°-130°)=100°.
【点睛】
本题考查对顶角,邻补角以及角平分线定义,主要考查学生的计算能力,熟练掌握角平分线的定义是解题的关键.
16. (2018·贵州初一期中)如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系,并说明理由;
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
【答案】(1) OF⊥OD,理由见解析;(2) 60°.
【解析】
(1)因为OF平分∠AOE,
所以∠AOF=∠EOF=∠AOE.
又因为∠DOE=∠BOD=∠BOE,
所以∠DOE+∠EOF=(∠BOE+∠AOE)= ×180°=90°,
即∠FOD=90°.
所以OF⊥OD.
(2)设∠AOC=x°,
因为∠AOC∶∠AOD=1∶5,
所以∠AOD=5x°.
因为∠AOC+∠AOD=180°,
所以x+5x=180,x=30.
所以∠DOE=∠BOD=∠AOC=30°.
又因为∠FOD=90°,
所以∠EOF=90°-30°=60°.
