2020年春季人教版数学七年级下册5.2平行线及其判定同步练习含解析
文档属性
| 名称 | 2020年春季人教版数学七年级下册5.2平行线及其判定同步练习含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 661.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-21 15:52:33 | ||
图片预览



文档简介
平行线及其判定
1. (2019·河北初一期末)下列说法正确的是( )
A.经过一点有无数条直线与已知直线平行
B.在同一平面内,有且只有一条直线与已知直线平行
C.经过直线外一点,有且只有一条直线与已知直线平行
D.以上说法都不正确
2. (2019·全国初一课时练习)若直线a∥b,b∥c,则a∥c的依据是( )
A.平行公理 B.等量代换
C.等式的性质 D.平行于同一条直线的两条直线平行
3. (2019·全国初一课时练习)如图,若AB∥CD,CD∥EF,那么AB和EF的位置关系是(?? )
A.平行 B.相交 C.垂直 D.不能确定
4. (2019·黑龙江初二期中)某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A.第一次左拐30°,第二次右拐30°
B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130°
D.第一次向左拐50°,第二次向左拐120°
5. (2018·贵州初一月考)如图,点E在CD的延长线上,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4 C.∠5=∠B D.∠B +∠BDC=180°
6. (2019·福建省永春第二中学初一期末)如图,点E在BC的延长线上,则下列条件中,能判定的是( )
A. B. C. D.
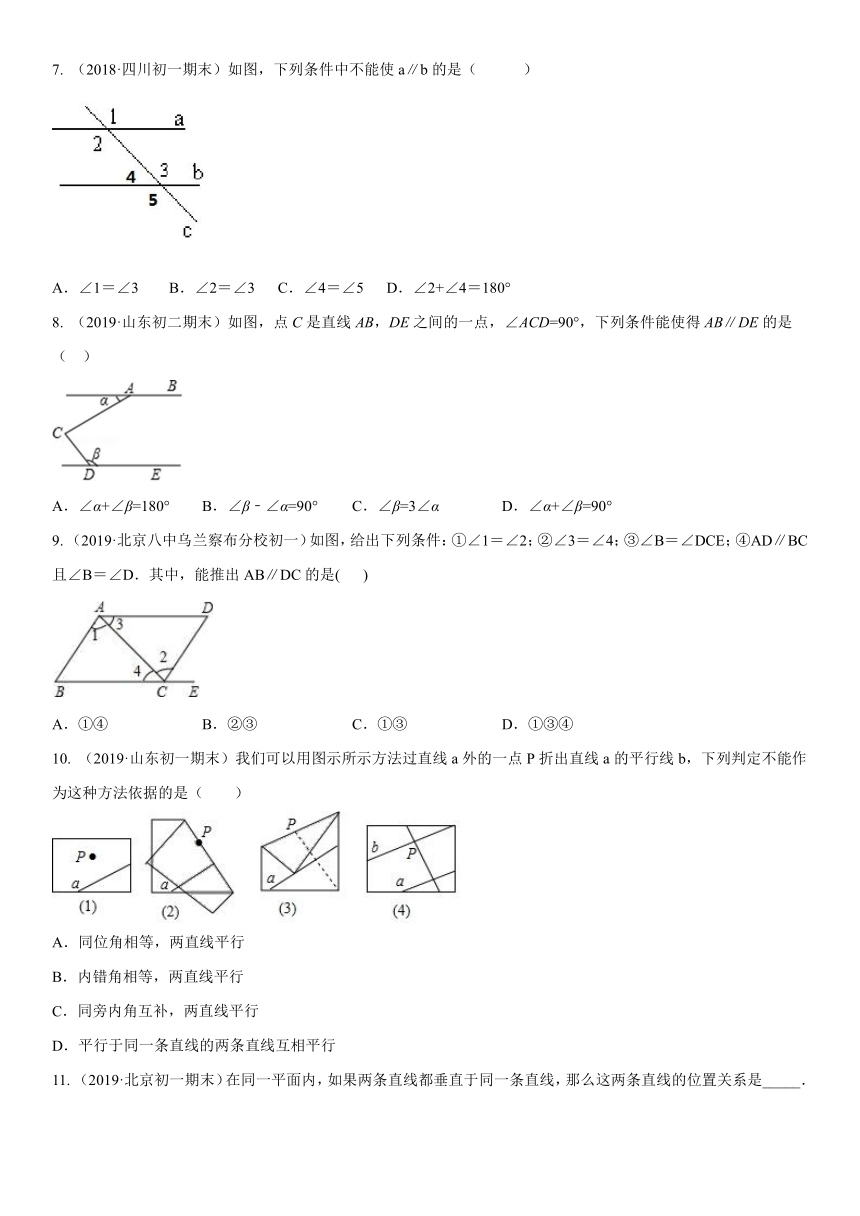
7. (2018·四川初一期末)如图,下列条件中不能使a∥b的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
8. (2019·山东初二期末)如图,点C是直线AB,DE之间的一点,∠ACD=90°,下列条件能使得AB∥DE的是( )
A.∠α+∠β=180° B.∠β﹣∠α=90° C.∠β=3∠α D.∠α+∠β=90°
9. (2019·北京八中乌兰察布分校初一)如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④AD∥BC且∠B=∠D.其中,能推出AB∥DC的是( )
A.①④ B.②③ C.①③ D.①③④
10. (2019·山东初一期末)我们可以用图示所示方法过直线a外的一点P折出直线a的平行线b,下列判定不能作为这种方法依据的是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.平行于同一条直线的两条直线互相平行
11. (2019·北京初一期末)在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线的位置关系是_____.
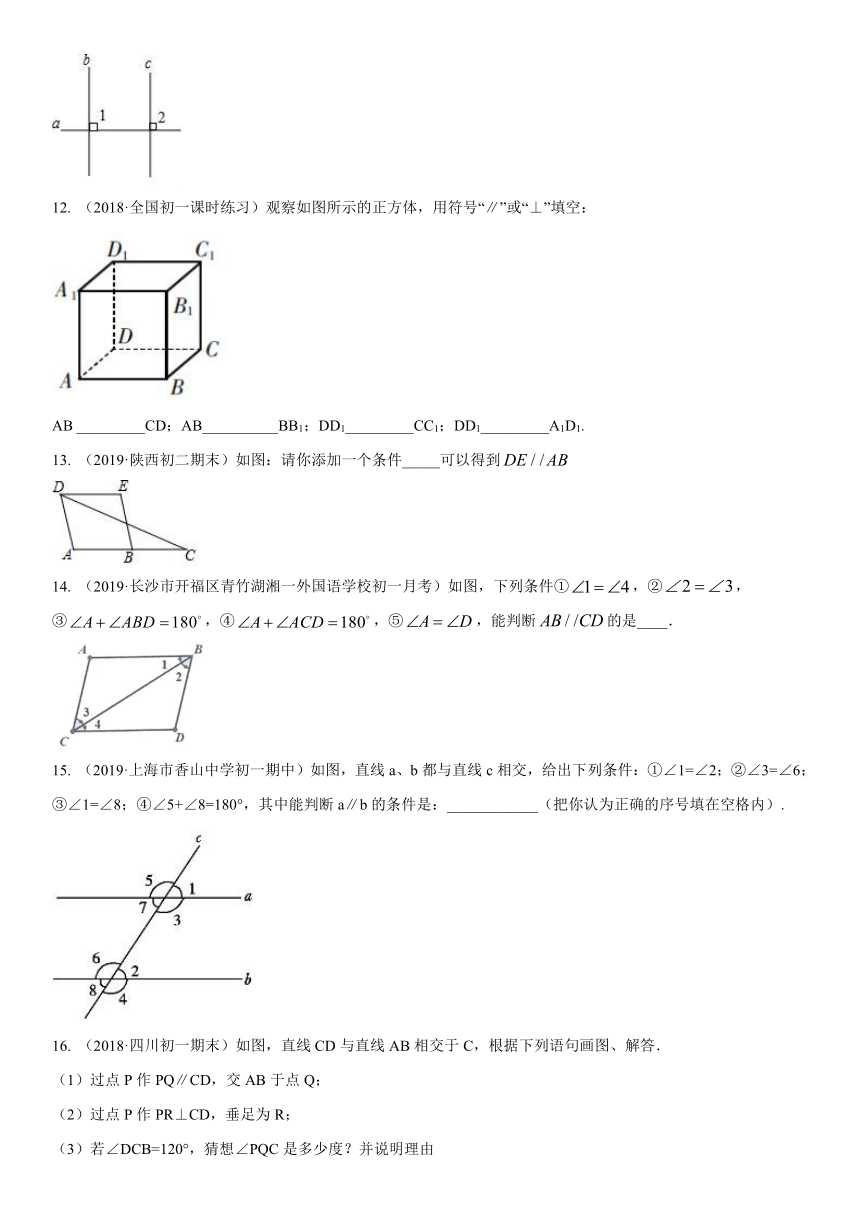
12. (2018·全国初一课时练习)观察如图所示的正方体,用符号“∥”或“⊥”填空:
AB _________CD;AB__________BB1;DD1_________CC1;DD1_________A1D1.
13. (2019·陕西初二期末)如图:请你添加一个条件_____可以得到
14. (2019·长沙市开福区青竹湖湘一外国语学校初一月考)如图,下列条件①,②,③,④,⑤,能判断的是____.
15. (2019·上海市香山中学初一期中)如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠1=∠8;④∠5+∠8=180°,其中能判断a∥b的条件是:____________(把你认为正确的序号填在空格内).
16. (2018·四川初一期末)如图,直线CD与直线AB相交于C,根据下列语句画图、解答.
(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由
17. (2019·肇庆市端州区南国中英文学校初一月考)如图,直线a,点B,点C.
(1)过点B画直线a的平行线,能画几条?
(2)过点C画直线a的平行线,它与过点B的平行线平行吗?
18. (2020·北京初三专题练习)下面是小明设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:如图1,直线BC及直线BC外一点P.
求作:直线PE,使得PE∥BC.
作法:如图2.
①在直线BC上取一点A,连接PA;
②作∠PAC的平分线AD;
③以点P为圆心,PA长为半径画弧,交射线AD于点E;
④作直线PE.
所以直线PE就是所求作的直线.根据小明设计的尺规作图过程.
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵AD平分∠PAC,
∴∠PAD=∠CAD.
∵PA=PE,
∴∠PAD= ,
∴∠PEA= ,
∴PE∥BC.( )(填推理依据).
答案
1. (2019·河北初一期末)下列说法正确的是( )
A.经过一点有无数条直线与已知直线平行
B.在同一平面内,有且只有一条直线与已知直线平行
C.经过直线外一点,有且只有一条直线与已知直线平行
D.以上说法都不正确
【答案】C
【解析】
解:A. 经过直线外一点有且只有一条直线与已知直线平行,所以错误,
B. 在同一平面内,(经过直线外一点)有且只有一条直线与已知直线平行,所以错误,
C. 经过直线外一点,有且只有一条直线与已知直线平行,正确.
故选C.
【点睛】
本题考查了平面内平行线的性质,属于简单题,熟悉概念是解题关键.
2. (2019·全国初一课时练习)若直线a∥b,b∥c,则a∥c的依据是( )
A.平行公理 B.等量代换
C.等式的性质 D.平行于同一条直线的两条直线平行
【答案】D
【解析】
因为直线a∥b,b∥c,所以a∥c的依据是平行于同一条直线的两条直线互相平行,
故选D.
3. (2019·全国初一课时练习)如图,若AB∥CD,CD∥EF,那么AB和EF的位置关系是(?? )
A.平行 B.相交 C.垂直 D.不能确定
【答案】A
【解析】
解:∵AB∥CD,CD∥EF,
∴AB∥EF,(平行线的传递性)
故选A.
【点睛】
本题考查了平行线的传递性,属于简单题,熟悉平行线的性质是解题关键.
4. (2019·黑龙江初二期中)某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A.第一次左拐30°,第二次右拐30°
B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130°
D.第一次向左拐50°,第二次向左拐120°
【答案】A
【解析】
如图所示(实线为行驶路线):
A符合“同位角相等,两直线平行”的判定,其余均不符合平行线的判定.
故选A.
【点睛】
本题考查平行线的判定,熟记定理是解决问题的关键.
5. (2018·贵州初一月考)如图,点E在CD的延长线上,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4 C.∠5=∠B D.∠B +∠BDC=180°
【答案】A
【解析】
解:选项A中,∠1=∠2,只可以判定AC//BD(内错角相等,两直线平行),所以A错误;
选项B中,∠3=∠4,可以判定AB//CD(内错角相等,两直线平行),所以正确;
选项C中,∠5=∠B,AB//CD(内错角相等,两直线平行),所以正确;
选项D中,∠B +∠BDC=180°,可以判定AB//CD(同旁内角互补,两直线平行),所以正确;
故答案为A.
【点睛】
本题考查平行的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键.
6. (2019·福建省永春第二中学初一期末)如图,点E在BC的延长线上,则下列条件中,能判定的是( )
A. B. C. D.
【答案】C
【解析】
解:A选项中,可判定,不符合题意;
B选项中,可判定,不符合题意;
C选项中,可判定,符合题意;
D选项中,可判定,不符合题意;
故答案为C.
【点睛】
此题主要考查平行线的判定方法,熟练掌握,即可解题.
7. (2018·四川初一期末)如图,下列条件中不能使a∥b的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
【答案】C
【解析】
A. ∠1=∠3,同位角相等,可判定a∥b;
B. ∠2=∠3,内错角相等,可判定a∥b;
C. ∠4=∠5,互为邻补角,不能判定a∥b;
D. ∠2+∠4=180°,同旁内角互补,可判定a∥b;
故选C.
【点睛】
此题主要考查平行线的判定方法,解题的关键是熟知平行线的判定定理.
8. (2019·山东初二期末)如图,点C是直线AB,DE之间的一点,∠ACD=90°,下列条件能使得AB∥DE的是( )
A.∠α+∠β=180° B.∠β﹣∠α=90° C.∠β=3∠α D.∠α+∠β=90°
【答案】B
【解析】
延长AC交DE于点F.
A. ∵∠α+∠β=180°,∠β=∠1+90°,
∴∠α=90°-∠1,即∠α≠∠1,
∴不能使得AB∥DE;
B. ∵∠β﹣∠α=90°,∠β=∠1+90°,
∴∠α=∠1,
∴能使得AB∥DE;
C.∵∠β=3∠α,∠β=∠1+90°,
∴3∠α=90°+∠1,即∠α≠∠1,
∴不能使得AB∥DE;
D.∵∠α+∠β=90°,∠β=∠1+90°,
∴∠α=-∠1,即∠α≠∠1,
∴不能使得AB∥DE;
故选B.
【点睛】
本题考查了平行线的判定方法:①两同位角相等,两直线平行;?②内错角相等,两直线平行;③同旁内角互补,两直线平行;④平行于同一直线的两条直线互相平行;同一平面内,垂直于同一直线的两条直线互相平行.
9. (2019·北京八中乌兰察布分校初一)如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④AD∥BC且∠B=∠D.其中,能推出AB∥DC的是( )
A.①④ B.②③ C.①③ D.①③④
【答案】D
【解析】
,;;,;
,,,,,
则符合题意的有,故选D.
10. (2019·山东初一期末)我们可以用图示所示方法过直线a外的一点P折出直线a的平行线b,下列判定不能作为这种方法依据的是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.平行于同一条直线的两条直线互相平行
【答案】D
【解析】
解:如图,由折叠可得,
∵∠BPC=∠ADP=90°,∴a∥b,故A选项能作为这种方法的依据;
∵∠EPD=∠ADP=90°,∴a∥b,故B选项能作为这种方法的依据;
∵∠BPD+∠ADP=180°,∴a∥b,故C选项能作为这种方法的依据;
而D选项不能作为这种方法的依据;
故选:D.
【点睛】
本题考查的是平行线的判定定理,解题时注意:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
11. (2019·北京初一期末)在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线的位置关系是_____.
【答案】b//c
【解析】
解:∵b⊥a, c⊥a,
∴b//c.
【点睛】
本题考查了平行线的性质,属于简单题,熟悉性质是解题关键.
12. (2018·全国初一课时练习)观察如图所示的正方体,用符号“∥”或“⊥”填空:
AB _________CD;AB__________BB1;DD1_________CC1;DD1_________A1D1.
【答案】∥; ⊥; ∥; ⊥.
【解析】
解:因为正方体每个面都是正方形,
正方形对边平行,相邻边垂直,
故分别填(1). ∥(2). ⊥(3). ∥ (4). ⊥.
【点睛】
掌握正方体的性质是解答本题的关键.
13. (2019·陕西初二期末)如图:请你添加一个条件_____可以得到
【答案】答案不唯一,当添加条件∠EDC=∠C或∠E=∠EBC或∠E+∠EBA=180°或∠A+∠ADE=180°时,都可以得到DE∥AB.
【解析】
由图可知,要使DE∥AB,可以添加以下条件:
(1)当∠EDC=∠C时,由“内错角相等,两直线平行”可得DE∥AB;
(2)当∠E=∠EBC时,由“内错角相等,两直线平行”可得DE∥AB;
(3)当∠E+∠EBA=180°时,由“同旁内角互补,两直线平行”可得DE∥AB;
(4)当∠A+∠ADE=180°时,由“同旁内角互补,两直线平行”可得DE∥AB.
故本题答案不唯一,当添加条件∠EDC=∠C或∠E=∠EBC或∠E+∠EBA=180°或∠A+∠ADE=180°时,都可以得到DE∥AB.
【点睛】
熟悉“平行线的判定方法”是解答本题的关键.
14. (2019·长沙市开福区青竹湖湘一外国语学校初一月考)如图,下列条件①,②,③,④,⑤,能判断的是____.
【答案】①④
【解析】
解:①,根据内错角相等可以判断.
②,得到的是AC∥BD,
③,得到的是AC∥BD,
④,可以判断.
⑤,判断不出平行,
所以答案是①④
【点睛】
本题考查了平行线的判定,属于简单题,熟悉平行线的判定定理,找到对应的内错角和同旁内角是解题关键.
15. (2019·上海市香山中学初一期中)如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠1=∠8;④∠5+∠8=180°,其中能判断a∥b的条件是:____________(把你认为正确的序号填在空格内).
【答案】①②④
【解析】
①∠1=∠2可根据同位角相等,两直线平行得到a∥b;
②∠3=∠6可根据内错角相等,两直线平行得到a∥b;
③∠1=∠4不能得到a∥b;
④∠3+∠2=180°,可根据同旁内角互补,两直线平行得到a∥b;
故答案为①②④.
【点睛】
本题考查平行线的判定,记住同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行,解题的关键是搞清楚同位角、内错角、同旁内角的概念
16. (2018·四川初一期末)如图,直线CD与直线AB相交于C,根据下列语句画图、解答.
(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由
【答案】(1)见解析;(2)见解析;(3)∠PQC=60°,理由见解析
【解析】
解:如图所示:
(1)画出如图直线PQ
(2)画出如图直线PR
(3)∠PQC=60°
理由是:因为PQ∥CD
所以∠DCB+∠PQC=180°
又因为∠DCB=120°
所以∠PQC=180°-120°=60°
17. (2019·肇庆市端州区南国中英文学校初一月考)如图,直线a,点B,点C.
(1)过点B画直线a的平行线,能画几条?
(2)过点C画直线a的平行线,它与过点B的平行线平行吗?
【答案】 (1)详见解析;(2)详见解析.
【解析】
(1)一条,如图,过直线a外的一点画直线a的平行线,有且只有一条直线与直线a平行;
(2)过点C画直线a的平行线,它与过点B的平行线平行.理由如下:
如图,∵b∥a,c∥a,∴c∥b.
【点睛】
此题重点考察学生对平行线的画法和性质的理解,掌握平行线的画法和性质是解题的关键.
18. (2020·北京初三专题练习)下面是小明设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:如图1,直线BC及直线BC外一点P.
求作:直线PE,使得PE∥BC.
作法:如图2.
①在直线BC上取一点A,连接PA;
②作∠PAC的平分线AD;
③以点P为圆心,PA长为半径画弧,交射线AD于点E;
④作直线PE.
所以直线PE就是所求作的直线.根据小明设计的尺规作图过程.
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵AD平分∠PAC,
∴∠PAD=∠CAD.
∵PA=PE,
∴∠PAD= ,
∴∠PEA= ,
∴PE∥BC.( )(填推理依据).
【答案】(1)详见解析;(2)∠PEA,∠CAD,内错角相等两直线平行.
【解析】
(1)如图所示:直线PE即为所求.
(2)证明:∵AD平分∠PAC,
∴∠PAD=∠CAD.
∵PA=PE,
∴∠PAD=∠PEA,
∴∠PEA=∠CAD,
∴PE∥BC.(内错角相等两直线平行).
故答案为:∠PEA,∠CAD,内错角相等两直线平行.
【点睛】
本题主要考查作图﹣复杂作图,解题的关键是掌握等腰三角形的性质和平行线的判定及角平分线的定义.
1. (2019·河北初一期末)下列说法正确的是( )
A.经过一点有无数条直线与已知直线平行
B.在同一平面内,有且只有一条直线与已知直线平行
C.经过直线外一点,有且只有一条直线与已知直线平行
D.以上说法都不正确
2. (2019·全国初一课时练习)若直线a∥b,b∥c,则a∥c的依据是( )
A.平行公理 B.等量代换
C.等式的性质 D.平行于同一条直线的两条直线平行
3. (2019·全国初一课时练习)如图,若AB∥CD,CD∥EF,那么AB和EF的位置关系是(?? )
A.平行 B.相交 C.垂直 D.不能确定
4. (2019·黑龙江初二期中)某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A.第一次左拐30°,第二次右拐30°
B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130°
D.第一次向左拐50°,第二次向左拐120°
5. (2018·贵州初一月考)如图,点E在CD的延长线上,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4 C.∠5=∠B D.∠B +∠BDC=180°
6. (2019·福建省永春第二中学初一期末)如图,点E在BC的延长线上,则下列条件中,能判定的是( )
A. B. C. D.
7. (2018·四川初一期末)如图,下列条件中不能使a∥b的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
8. (2019·山东初二期末)如图,点C是直线AB,DE之间的一点,∠ACD=90°,下列条件能使得AB∥DE的是( )
A.∠α+∠β=180° B.∠β﹣∠α=90° C.∠β=3∠α D.∠α+∠β=90°
9. (2019·北京八中乌兰察布分校初一)如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④AD∥BC且∠B=∠D.其中,能推出AB∥DC的是( )
A.①④ B.②③ C.①③ D.①③④
10. (2019·山东初一期末)我们可以用图示所示方法过直线a外的一点P折出直线a的平行线b,下列判定不能作为这种方法依据的是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.平行于同一条直线的两条直线互相平行
11. (2019·北京初一期末)在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线的位置关系是_____.
12. (2018·全国初一课时练习)观察如图所示的正方体,用符号“∥”或“⊥”填空:
AB _________CD;AB__________BB1;DD1_________CC1;DD1_________A1D1.
13. (2019·陕西初二期末)如图:请你添加一个条件_____可以得到
14. (2019·长沙市开福区青竹湖湘一外国语学校初一月考)如图,下列条件①,②,③,④,⑤,能判断的是____.
15. (2019·上海市香山中学初一期中)如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠1=∠8;④∠5+∠8=180°,其中能判断a∥b的条件是:____________(把你认为正确的序号填在空格内).
16. (2018·四川初一期末)如图,直线CD与直线AB相交于C,根据下列语句画图、解答.
(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由
17. (2019·肇庆市端州区南国中英文学校初一月考)如图,直线a,点B,点C.
(1)过点B画直线a的平行线,能画几条?
(2)过点C画直线a的平行线,它与过点B的平行线平行吗?
18. (2020·北京初三专题练习)下面是小明设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:如图1,直线BC及直线BC外一点P.
求作:直线PE,使得PE∥BC.
作法:如图2.
①在直线BC上取一点A,连接PA;
②作∠PAC的平分线AD;
③以点P为圆心,PA长为半径画弧,交射线AD于点E;
④作直线PE.
所以直线PE就是所求作的直线.根据小明设计的尺规作图过程.
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵AD平分∠PAC,
∴∠PAD=∠CAD.
∵PA=PE,
∴∠PAD= ,
∴∠PEA= ,
∴PE∥BC.( )(填推理依据).
答案
1. (2019·河北初一期末)下列说法正确的是( )
A.经过一点有无数条直线与已知直线平行
B.在同一平面内,有且只有一条直线与已知直线平行
C.经过直线外一点,有且只有一条直线与已知直线平行
D.以上说法都不正确
【答案】C
【解析】
解:A. 经过直线外一点有且只有一条直线与已知直线平行,所以错误,
B. 在同一平面内,(经过直线外一点)有且只有一条直线与已知直线平行,所以错误,
C. 经过直线外一点,有且只有一条直线与已知直线平行,正确.
故选C.
【点睛】
本题考查了平面内平行线的性质,属于简单题,熟悉概念是解题关键.
2. (2019·全国初一课时练习)若直线a∥b,b∥c,则a∥c的依据是( )
A.平行公理 B.等量代换
C.等式的性质 D.平行于同一条直线的两条直线平行
【答案】D
【解析】
因为直线a∥b,b∥c,所以a∥c的依据是平行于同一条直线的两条直线互相平行,
故选D.
3. (2019·全国初一课时练习)如图,若AB∥CD,CD∥EF,那么AB和EF的位置关系是(?? )
A.平行 B.相交 C.垂直 D.不能确定
【答案】A
【解析】
解:∵AB∥CD,CD∥EF,
∴AB∥EF,(平行线的传递性)
故选A.
【点睛】
本题考查了平行线的传递性,属于简单题,熟悉平行线的性质是解题关键.
4. (2019·黑龙江初二期中)某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是( )
A.第一次左拐30°,第二次右拐30°
B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130°
D.第一次向左拐50°,第二次向左拐120°
【答案】A
【解析】
如图所示(实线为行驶路线):
A符合“同位角相等,两直线平行”的判定,其余均不符合平行线的判定.
故选A.
【点睛】
本题考查平行线的判定,熟记定理是解决问题的关键.
5. (2018·贵州初一月考)如图,点E在CD的延长线上,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4 C.∠5=∠B D.∠B +∠BDC=180°
【答案】A
【解析】
解:选项A中,∠1=∠2,只可以判定AC//BD(内错角相等,两直线平行),所以A错误;
选项B中,∠3=∠4,可以判定AB//CD(内错角相等,两直线平行),所以正确;
选项C中,∠5=∠B,AB//CD(内错角相等,两直线平行),所以正确;
选项D中,∠B +∠BDC=180°,可以判定AB//CD(同旁内角互补,两直线平行),所以正确;
故答案为A.
【点睛】
本题考查平行的判定,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键.
6. (2019·福建省永春第二中学初一期末)如图,点E在BC的延长线上,则下列条件中,能判定的是( )
A. B. C. D.
【答案】C
【解析】
解:A选项中,可判定,不符合题意;
B选项中,可判定,不符合题意;
C选项中,可判定,符合题意;
D选项中,可判定,不符合题意;
故答案为C.
【点睛】
此题主要考查平行线的判定方法,熟练掌握,即可解题.
7. (2018·四川初一期末)如图,下列条件中不能使a∥b的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
【答案】C
【解析】
A. ∠1=∠3,同位角相等,可判定a∥b;
B. ∠2=∠3,内错角相等,可判定a∥b;
C. ∠4=∠5,互为邻补角,不能判定a∥b;
D. ∠2+∠4=180°,同旁内角互补,可判定a∥b;
故选C.
【点睛】
此题主要考查平行线的判定方法,解题的关键是熟知平行线的判定定理.
8. (2019·山东初二期末)如图,点C是直线AB,DE之间的一点,∠ACD=90°,下列条件能使得AB∥DE的是( )
A.∠α+∠β=180° B.∠β﹣∠α=90° C.∠β=3∠α D.∠α+∠β=90°
【答案】B
【解析】
延长AC交DE于点F.
A. ∵∠α+∠β=180°,∠β=∠1+90°,
∴∠α=90°-∠1,即∠α≠∠1,
∴不能使得AB∥DE;
B. ∵∠β﹣∠α=90°,∠β=∠1+90°,
∴∠α=∠1,
∴能使得AB∥DE;
C.∵∠β=3∠α,∠β=∠1+90°,
∴3∠α=90°+∠1,即∠α≠∠1,
∴不能使得AB∥DE;
D.∵∠α+∠β=90°,∠β=∠1+90°,
∴∠α=-∠1,即∠α≠∠1,
∴不能使得AB∥DE;
故选B.
【点睛】
本题考查了平行线的判定方法:①两同位角相等,两直线平行;?②内错角相等,两直线平行;③同旁内角互补,两直线平行;④平行于同一直线的两条直线互相平行;同一平面内,垂直于同一直线的两条直线互相平行.
9. (2019·北京八中乌兰察布分校初一)如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④AD∥BC且∠B=∠D.其中,能推出AB∥DC的是( )
A.①④ B.②③ C.①③ D.①③④
【答案】D
【解析】
,;;,;
,,,,,
则符合题意的有,故选D.
10. (2019·山东初一期末)我们可以用图示所示方法过直线a外的一点P折出直线a的平行线b,下列判定不能作为这种方法依据的是( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.平行于同一条直线的两条直线互相平行
【答案】D
【解析】
解:如图,由折叠可得,
∵∠BPC=∠ADP=90°,∴a∥b,故A选项能作为这种方法的依据;
∵∠EPD=∠ADP=90°,∴a∥b,故B选项能作为这种方法的依据;
∵∠BPD+∠ADP=180°,∴a∥b,故C选项能作为这种方法的依据;
而D选项不能作为这种方法的依据;
故选:D.
【点睛】
本题考查的是平行线的判定定理,解题时注意:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
11. (2019·北京初一期末)在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线的位置关系是_____.
【答案】b//c
【解析】
解:∵b⊥a, c⊥a,
∴b//c.
【点睛】
本题考查了平行线的性质,属于简单题,熟悉性质是解题关键.
12. (2018·全国初一课时练习)观察如图所示的正方体,用符号“∥”或“⊥”填空:
AB _________CD;AB__________BB1;DD1_________CC1;DD1_________A1D1.
【答案】∥; ⊥; ∥; ⊥.
【解析】
解:因为正方体每个面都是正方形,
正方形对边平行,相邻边垂直,
故分别填(1). ∥(2). ⊥(3). ∥ (4). ⊥.
【点睛】
掌握正方体的性质是解答本题的关键.
13. (2019·陕西初二期末)如图:请你添加一个条件_____可以得到
【答案】答案不唯一,当添加条件∠EDC=∠C或∠E=∠EBC或∠E+∠EBA=180°或∠A+∠ADE=180°时,都可以得到DE∥AB.
【解析】
由图可知,要使DE∥AB,可以添加以下条件:
(1)当∠EDC=∠C时,由“内错角相等,两直线平行”可得DE∥AB;
(2)当∠E=∠EBC时,由“内错角相等,两直线平行”可得DE∥AB;
(3)当∠E+∠EBA=180°时,由“同旁内角互补,两直线平行”可得DE∥AB;
(4)当∠A+∠ADE=180°时,由“同旁内角互补,两直线平行”可得DE∥AB.
故本题答案不唯一,当添加条件∠EDC=∠C或∠E=∠EBC或∠E+∠EBA=180°或∠A+∠ADE=180°时,都可以得到DE∥AB.
【点睛】
熟悉“平行线的判定方法”是解答本题的关键.
14. (2019·长沙市开福区青竹湖湘一外国语学校初一月考)如图,下列条件①,②,③,④,⑤,能判断的是____.
【答案】①④
【解析】
解:①,根据内错角相等可以判断.
②,得到的是AC∥BD,
③,得到的是AC∥BD,
④,可以判断.
⑤,判断不出平行,
所以答案是①④
【点睛】
本题考查了平行线的判定,属于简单题,熟悉平行线的判定定理,找到对应的内错角和同旁内角是解题关键.
15. (2019·上海市香山中学初一期中)如图,直线a、b都与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠1=∠8;④∠5+∠8=180°,其中能判断a∥b的条件是:____________(把你认为正确的序号填在空格内).
【答案】①②④
【解析】
①∠1=∠2可根据同位角相等,两直线平行得到a∥b;
②∠3=∠6可根据内错角相等,两直线平行得到a∥b;
③∠1=∠4不能得到a∥b;
④∠3+∠2=180°,可根据同旁内角互补,两直线平行得到a∥b;
故答案为①②④.
【点睛】
本题考查平行线的判定,记住同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行,解题的关键是搞清楚同位角、内错角、同旁内角的概念
16. (2018·四川初一期末)如图,直线CD与直线AB相交于C,根据下列语句画图、解答.
(1)过点P作PQ∥CD,交AB于点Q;
(2)过点P作PR⊥CD,垂足为R;
(3)若∠DCB=120°,猜想∠PQC是多少度?并说明理由
【答案】(1)见解析;(2)见解析;(3)∠PQC=60°,理由见解析
【解析】
解:如图所示:
(1)画出如图直线PQ
(2)画出如图直线PR
(3)∠PQC=60°
理由是:因为PQ∥CD
所以∠DCB+∠PQC=180°
又因为∠DCB=120°
所以∠PQC=180°-120°=60°
17. (2019·肇庆市端州区南国中英文学校初一月考)如图,直线a,点B,点C.
(1)过点B画直线a的平行线,能画几条?
(2)过点C画直线a的平行线,它与过点B的平行线平行吗?
【答案】 (1)详见解析;(2)详见解析.
【解析】
(1)一条,如图,过直线a外的一点画直线a的平行线,有且只有一条直线与直线a平行;
(2)过点C画直线a的平行线,它与过点B的平行线平行.理由如下:
如图,∵b∥a,c∥a,∴c∥b.
【点睛】
此题重点考察学生对平行线的画法和性质的理解,掌握平行线的画法和性质是解题的关键.
18. (2020·北京初三专题练习)下面是小明设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:如图1,直线BC及直线BC外一点P.
求作:直线PE,使得PE∥BC.
作法:如图2.
①在直线BC上取一点A,连接PA;
②作∠PAC的平分线AD;
③以点P为圆心,PA长为半径画弧,交射线AD于点E;
④作直线PE.
所以直线PE就是所求作的直线.根据小明设计的尺规作图过程.
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:∵AD平分∠PAC,
∴∠PAD=∠CAD.
∵PA=PE,
∴∠PAD= ,
∴∠PEA= ,
∴PE∥BC.( )(填推理依据).
【答案】(1)详见解析;(2)∠PEA,∠CAD,内错角相等两直线平行.
【解析】
(1)如图所示:直线PE即为所求.
(2)证明:∵AD平分∠PAC,
∴∠PAD=∠CAD.
∵PA=PE,
∴∠PAD=∠PEA,
∴∠PEA=∠CAD,
∴PE∥BC.(内错角相等两直线平行).
故答案为:∠PEA,∠CAD,内错角相等两直线平行.
【点睛】
本题主要考查作图﹣复杂作图,解题的关键是掌握等腰三角形的性质和平行线的判定及角平分线的定义.
