2020年春季人教版数学七年级下册5.3平行线的性质同步练习含解析
文档属性
| 名称 | 2020年春季人教版数学七年级下册5.3平行线的性质同步练习含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 723.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-21 15:57:31 | ||
图片预览




文档简介
平行线的性质
1. (2020·辽宁初二期末)下列命题中的假命题是( )
A.两直线平行,内错角相等 B.同位角相等,两直线平行
C.两直线平行,同旁内角相等 D.平行于同一条直线的两直线平行
2. (2020·上海初三专题练习)如图,直线l1∥l2,如果∠1=30°,∠2=50°,那么∠3=( )
A.20° B.80° C.90° D.100°
3. (2020·沈阳市第二十三中学初一期中)如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
A.10° B.15° C.20° D.25°
4. (2020·北京初三专题练习)如图,AB∥CD,DA⊥CE于点A.若∠D=35°,则∠EAB的度数为( )
A.35° B.45° C.55° D.65°
5. (2020·北京初三专题练习)如图,直线,直线EF分别与AB,CD交于点E,F,EG平分,交CD于点G,若,则的度数是( )
A.60° B.55° C.50° D.45°
6. (2020·北京初三专题练习)如图,将一张矩形纸片折叠,若∠1=80°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
7. (2020·全国初三专题练习)如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )
A.80° B.90° C.100° D.105°
8. (2019·浙江初二月考)下列句子属于命题的是( ).
A.正数大于一切负数吗? B.钝角大于直角
C.将开平方 D.作线段的中点
9. (2020·四川初二月考)下列命题中,其逆命题是假命题的是( ?)
A.若ab=1,则a与b互为倒数 B.如果|a|=|b|,那么a2=b2
C.等腰三角形的两个底角相等 D.若两个数的差为正数,则这两个数都为正数
10. (2019·上海市南洋模范中学初二月考)下列定理中,没有逆定理的是( )
A.两直线平行,同旁内角互补; B.两个全等三角形的对应角相等
C.直角三角形的两个锐角互余; D.两内角相等的三角形是等腰三角形
11. (2019·福建初一期末)在俄罗斯方块游戏中,若某行被小方格块填满,则该行中的所有小方格会自动消失.现在游戏
机屏幕下面三行已拼成如图所示的图案,屏幕上方又出现一小方格块正向下运动,为了使屏幕下面三行中的小方格都自动消失,你可以进行以下哪项操作( )
A.先逆时针旋转90°,再向左平移 B.先顺时针旋转90°,再向左平移
C.先逆时针旋转90°,再向右平移 D.先顺时针旋转90°,再向右平移
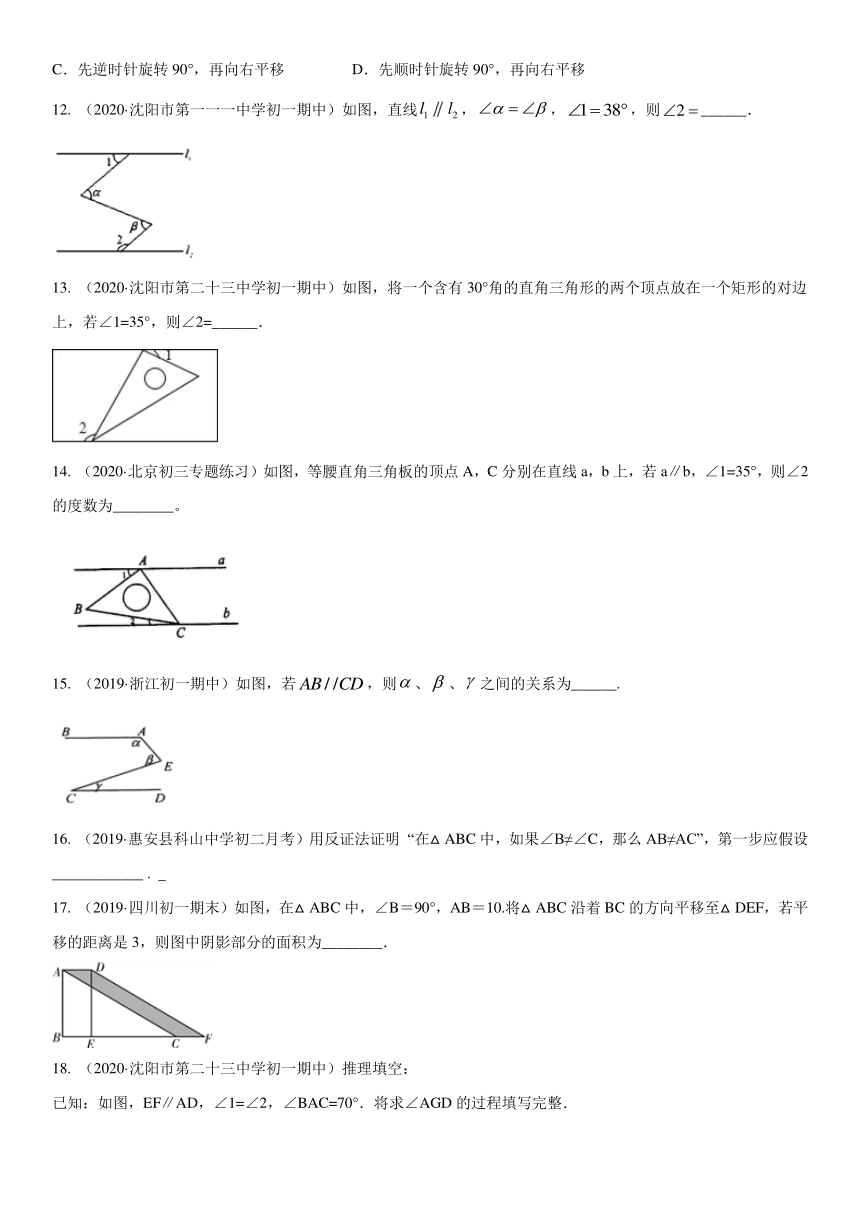
12. (2020·沈阳市第一一一中学初一期中)如图,直线,,,则______.
13. (2020·沈阳市第二十三中学初一期中)如图,将一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=35°,则∠2=______.
14. (2020·北京初三专题练习)如图,等腰直角三角板的顶点A,C分别在直线a,b上,若a∥b,∠1=35°,则∠2的度数为________。
15. (2019·浙江初一期中)如图,若,则、、之间的关系为______.
16. (2019·惠安县科山中学初二月考)用反证法证明 “在△ABC中,如果∠B≠∠C,那么AB≠AC”,第一步应假设____________ .
17. (2019·四川初一期末)如图,在△ABC中,∠B=90°,AB=10.将△ABC沿着BC的方向平移至△DEF,若平移的距离是3,则图中阴影部分的面积为________.
18. (2020·沈阳市第二十三中学初一期中)推理填空:
已知:如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
证明:∵EF∥AD,( )
∴∠2= . ( )
∵∠1=∠2,( )
∴∠1=∠3.( )
∴AB∥DG.( )
∴∠BAC+ =180°( )
又∵∠BAC=70°,( )
∴∠AGD= .
19. (2019·湖北初一期中)如图,D,E为△ABC边AB上两点,F,H分别在AC,BC上,∠1+∠2=180°
(1)求证:EF∥DH;
(2)若∠ACB=90°,∠DHB=25°,求∠EFC的度数.
20. (2020·沈阳市第一一一中学初一期中)已知△ABC,∠ACB=90°.
(1)如图1,CD⊥AB于点D,AC=5cm,BC=12cm,AB=13cm,求点C到AB的距离;
(2)如图2,x 轴⊥y轴 , DM⊥y轴,若∠AOG=50°,求∠CEF的度数;
(3)如图3,x 轴⊥y轴,DM⊥y轴,旋转△ABC,使∠C的顶点C在直线DM与x轴之间,N为线段AO上一点,E为BC与DM的交点,F为AB与DM的交点,且∠NEC+∠CEF=180°,下列两个结论:①NEF﹣∠AOG为定值;②NEF/∠AOG为定值,其中只有一个是正确的,请你判断出正确的结论,并求其值.
答案
1. (2020·辽宁初二期末)下列命题中的假命题是( )
A.两直线平行,内错角相等 B.同位角相等,两直线平行
C.两直线平行,同旁内角相等 D.平行于同一条直线的两直线平行
【答案】C
【解析】
A、两直线平行,内错角相等,所以A选项为真命题;
B、同位角相等,两直线平行,所以B选项为真命题;
C、两直线平行,同旁内角互补角,所以C选项为假命题;
D、平行于同一条直线的两直线平行,所以D选项为真命题.
故选C.
【点睛】
本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 有些命题的正确性是用推理证实的,这样的真命题叫做定理.
2. (2020·上海初三专题练习)如图,直线l1∥l2,如果∠1=30°,∠2=50°,那么∠3=( )
A.20° B.80° C.90° D.100°
【答案】B
【解析】
解:过∠3的顶点作l1的平行线m,
∴∠1=∠4,
∵l1∥l2
∴m∥l2,
∴∠2=∠5
∴∠3=∠4+∠5=∠1+∠2=80°
故选:B.
【点睛】
本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.
3. (2020·沈阳市第二十三中学初一期中)如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
A.10° B.15° C.20° D.25°
【答案】D
【解析】
∵AB∥CD, ∴∠3=∠1=65°, ∴∠2=180°﹣∠3﹣90°=180°﹣65°﹣90°=25°.
4. (2020·北京初三专题练习)如图,AB∥CD,DA⊥CE于点A.若∠D=35°,则∠EAB的度数为( )
A.35° B.45° C.55° D.65°
【答案】C
【解析】
∵AB∥CD,
∴∠BAD=∠D=35°,
∵DA⊥CE,
∴∠DAE=90°,
∴∠EAB=55°.
故选:C.
【点睛】
本题主要考查了平行线的性质以及垂线的定义,解题时注意:两直线平行,内错角相等.
5. (2020·北京初三专题练习)如图,直线,直线EF分别与AB,CD交于点E,F,EG平分,交CD于点G,若,则的度数是( )
A.60° B.55° C.50° D.45°
【答案】B
【解析】
,
,
,
,
,
,
,
故选.
【点睛】
本题主要考查了平行线的性质的应用,角平分线的应用,证出是解题关键.
6. (2020·北京初三专题练习)如图,将一张矩形纸片折叠,若∠1=80°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
【答案】A
【解析】
如图,
∵a∥b,
∴∠1=∠3=80°,
由翻折不变性可知:∠2=∠4= QUOTE EMBED Equation.DSMT4 (180°﹣80°)=50°,
故选A.
【点睛】
本题考查平行线的性质,解题的关键是熟练掌握基本知识.
7. (2020·全国初三专题练习)如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )
A.80° B.90° C.100° D.105°
【答案】A
【解析】
解:由题意可得:AN∥FB,EC∥BD,
∴∠NAB=∠FBD=75°,
∵∠CBF=25°,
∴∠CBD=100°,
则∠ECB=180°-100°=80°.
故选:A.
【点睛】
本题考查方向角,正确得出平行线,利用平行线的性质是解题关键.
8. (2019·浙江初二月考)下列句子属于命题的是( ).
A.正数大于一切负数吗? B.钝角大于直角
C.将开平方 D.作线段的中点
【答案】B
【解析】
A 、正数大于一切负数吗?为疑问句,它不是命题,所以A选项错误;
B 、钝角大于直角是命题,所以B选项正确;
C、将16开平方为陈述句,它不是命题,所以C选项错误;
D 、作线段AB的中点为陈述句,它不是命题,所以D选项错误,
故选 B .
9. (2020·四川初二月考)下列命题中,其逆命题是假命题的是( ?)
A.若ab=1,则a与b互为倒数 B.如果|a|=|b|,那么a2=b2
C.等腰三角形的两个底角相等 D.若两个数的差为正数,则这两个数都为正数
【答案】D
【解析】
解:A、若a与b互为倒数,则ab=1;故A的逆命题是真命题;
B、如果a2=b2,则|a|=|b|;故B的逆命题是真命题;
C、如果三角形的两个底角相等,那么这个三角形是等腰三角形;故C的逆命题是真命题;
D、若两个数是正数,那么这两个数的差为正数;故D的逆命题是假命题;
故选择:D.
【点睛】
此题考查了命题与逆命题的关系.解题的关键是找到各命题的逆命题,再证明正误即可.
10. (2019·上海市南洋模范中学初二月考)下列定理中,没有逆定理的是( )
A.两直线平行,同旁内角互补; B.两个全等三角形的对应角相等
C.直角三角形的两个锐角互余; D.两内角相等的三角形是等腰三角形
【答案】B
【解析】
A.其逆命题是“同旁内角互补,两直线平行”,正确,所以有逆定理;
B.其逆命题是“对应角相等的三角形是全等三角形”,错误,所以没有逆定理;
C.其逆命题是“两个锐角互余的三角形是直角三角形”,正确,所以有逆定理;
D.其逆命题是“等腰三角形的两个内角相等”,正确,所以有逆定理.
故选B.
【点睛】
本题考查了命题与定理的区别,正确的命题叫定理.
11. (2019·福建初一期末)在俄罗斯方块游戏中,若某行被小方格块填满,则该行中的所有小方格会自动消失.现在游戏
机屏幕下面三行已拼成如图所示的图案,屏幕上方又出现一小方格块正向下运动,为了使屏幕下面三行中的小方格都自动消失,你可以进行以下哪项操作( )
A.先逆时针旋转90°,再向左平移 B.先顺时针旋转90°,再向左平移
C.先逆时针旋转90°,再向右平移 D.先顺时针旋转90°,再向右平移
【答案】A
【解析】
屏幕上方又出现一小方格块正向下运动,为了使屏幕下面三行中的小方格都自动消失,可以先逆时针旋转90°,再向左平移.
故选A.
12. (2020·沈阳市第一一一中学初一期中)如图,直线,,,则______.
【答案】142°.
【解析】
如图延长直接交l1,其夹角为∠3,
∵∠α=∠β,
∴∠3=∠1=38°
∵l1∥l2,
∴∠2=180°-∠3=142°.
【点睛】
此题主要考查平行线的性质,解题的关键是根据题意作出辅助线.
13. (2020·沈阳市第二十三中学初一期中)如图,将一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=35°,则∠2=______.
【答案】125°
【解析】
解:如图,
∵∠1+∠3+90°=180°,∠1=35°,
∴∠3=90°-35°=55°.
∵矩形对边平行,
∴∠2+∠3=180°,
∴∠2=180°-∠3=125°.
故答案为:125°.
【点睛】
本题考查了平行线的性质以及平角定义,解题关键是根据两直线平行,同旁内角互补解答问题.
14. (2020·北京初三专题练习)如图,等腰直角三角板的顶点A,C分别在直线a,b上,若a∥b,∠1=35°,则∠2的度数为________。
【答案】10°
【解析】
解:如图,
由题意可知
又
故答案是10°
【点睛】
本题考察两直线平行,内错角相等,灵活运用等腰直角三角形中的角是解题的关键.
15. (2019·浙江初一期中)如图,若,则、、之间的关系为______.
【答案】
【解析】
过点E作EF∥AB,如图所示.
∵AB∥CD,EF∥AB,
∴EF∥CD∥AB,
∴∠α+∠AEF=180°,∠γ=∠CEF.
又∵∠AEF+∠CEF=∠β,
∴∠α+∠β?∠γ=180°.
故答案为∠α+∠β?∠γ=180°.
【点睛】
考查平行公理以及平行线的性质,掌握平行线的性质是解题的关键.
16. (2019·惠安县科山中学初二月考)用反证法证明 “在△ABC中,如果∠B≠∠C,那么AB≠AC”,第一步应假设____________ .
【答案】AB=AC
【解析】
解:用反证法证明命题“在△ABC中,∠B≠∠C,那么AB≠AC”的过程中,
第一步应是假设AB=AC.
故答案为:AB=AC.
【点睛】
本题结合角的比较考查反证法,解此题关键要懂得反证法的意义及步骤.
反证法的步骤是:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
17. (2019·四川初一期末)如图,在△ABC中,∠B=90°,AB=10.将△ABC沿着BC的方向平移至△DEF,若平移的距离是3,则图中阴影部分的面积为________.
【答案】30
【解析】
解:∵直角△ABC沿BC边平移3个单位得到直角△DEF,∴AC=DF,AD=CF=3,∴四边形ACFD为平行四边形,∴S平行四边形ACFD=CF?AB=3×10=30,即阴影部分的面积为30.故答案为:30.
点睛:本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.也考查了平行四边形的面积公式.
18. (2020·沈阳市第二十三中学初一期中)推理填空:
已知:如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
证明:∵EF∥AD,( )
∴∠2= . ( )
∵∠1=∠2,( )
∴∠1=∠3.( )
∴AB∥DG.( )
∴∠BAC+ =180°( )
又∵∠BAC=70°,( )
∴∠AGD= .
【答案】见解析
【解析】
解:(1)∵EF∥AD,(已知)
∴∠2=∠3.(两直线平行,同位角相等)
又∵∠1=∠2,(已知)
∴∠1=∠3.(等量代换)
∴AB∥DG.(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°.(两直线平行,同旁内角互补)
又∵∠BAC=70°,(已知)
∴∠AGD=110°.
【点睛】
本题考查了平行线的判定与性质;熟练掌握平行线的判定与性质是解答关键.
19. (2019·湖北初一期中)如图,D,E为△ABC边AB上两点,F,H分别在AC,BC上,∠1+∠2=180°
(1)求证:EF∥DH;
(2)若∠ACB=90°,∠DHB=25°,求∠EFC的度数.
【答案】(1)见解析;(2)∠EFC=115°.
【解析】
(1)证明:∵∠1+∠2=180°,∠ADH+∠2=180°,
∴∠1=∠ADH,
∴EF∥DH;
(2)解:过点C作CG∥DH,交AB于G,如图所示:
则∠GCB=∠DHB=25°,
∴∠ACG=∠ACB﹣∠GCB=90°﹣25°=65°,
由(1)得:EF∥DH,
∴CG∥EF,
∴∠EFC+∠ACG=180°,
∴∠EFC=180°﹣∠ACG=180°﹣65°=115°.
【点睛】
本题考查了平行线的判定与性质,熟练掌握平行线的性质是解题的关键.
20. (2020·沈阳市第一一一中学初一期中)已知△ABC,∠ACB=90°.
(1)如图1,CD⊥AB于点D,AC=5cm,BC=12cm,AB=13cm,求点C到AB的距离;
(2)如图2,x 轴⊥y轴 , DM⊥y轴,若∠AOG=50°,求∠CEF的度数;
(3)如图3,x 轴⊥y轴,DM⊥y轴,旋转△ABC,使∠C的顶点C在直线DM与x轴之间,N为线段AO上一点,E为BC与DM的交点,F为AB与DM的交点,且∠NEC+∠CEF=180°,下列两个结论:①NEF﹣∠AOG为定值;②NEF/∠AOG为定值,其中只有一个是正确的,请你判断出正确的结论,并求其值.
【答案】(1);(2)∠CEF=140°;(3),是定值
【解析】
解:(1)∵AC⊥BC,BC=12cm,
∴AC
∴
∴
∴点C到AB的距离为
故答案为:
(2)∵∠AOG=50°,
∴∠POD=50°,
∴∠COD=40°,
∴∠CQO=50°,
∴∠DQE=50°,
∴∠CED=40°,
∴∠CEF=140°;
(3)为定值.理由如下:
作CP∥x轴,如图3,
∵CP∥DM∥x轴,
∴∠AOG=∠1,∠2+∠CEF=180°,
而∠NEC+∠CEF=180°,
∴∠2=∠NEC,
∵∠1+∠2=90°,
∠NEF+2∠2=180°,
∴∠NEF=2∠1=2∠AOG,
∴,是定值.
【点睛】
此题考查了平行线的判定与性质:平行线于同一条直线的两直线平行;两直线平行,同位角相等;两直线平行,同旁内角互补.
1. (2020·辽宁初二期末)下列命题中的假命题是( )
A.两直线平行,内错角相等 B.同位角相等,两直线平行
C.两直线平行,同旁内角相等 D.平行于同一条直线的两直线平行
2. (2020·上海初三专题练习)如图,直线l1∥l2,如果∠1=30°,∠2=50°,那么∠3=( )
A.20° B.80° C.90° D.100°
3. (2020·沈阳市第二十三中学初一期中)如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
A.10° B.15° C.20° D.25°
4. (2020·北京初三专题练习)如图,AB∥CD,DA⊥CE于点A.若∠D=35°,则∠EAB的度数为( )
A.35° B.45° C.55° D.65°
5. (2020·北京初三专题练习)如图,直线,直线EF分别与AB,CD交于点E,F,EG平分,交CD于点G,若,则的度数是( )
A.60° B.55° C.50° D.45°
6. (2020·北京初三专题练习)如图,将一张矩形纸片折叠,若∠1=80°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
7. (2020·全国初三专题练习)如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )
A.80° B.90° C.100° D.105°
8. (2019·浙江初二月考)下列句子属于命题的是( ).
A.正数大于一切负数吗? B.钝角大于直角
C.将开平方 D.作线段的中点
9. (2020·四川初二月考)下列命题中,其逆命题是假命题的是( ?)
A.若ab=1,则a与b互为倒数 B.如果|a|=|b|,那么a2=b2
C.等腰三角形的两个底角相等 D.若两个数的差为正数,则这两个数都为正数
10. (2019·上海市南洋模范中学初二月考)下列定理中,没有逆定理的是( )
A.两直线平行,同旁内角互补; B.两个全等三角形的对应角相等
C.直角三角形的两个锐角互余; D.两内角相等的三角形是等腰三角形
11. (2019·福建初一期末)在俄罗斯方块游戏中,若某行被小方格块填满,则该行中的所有小方格会自动消失.现在游戏
机屏幕下面三行已拼成如图所示的图案,屏幕上方又出现一小方格块正向下运动,为了使屏幕下面三行中的小方格都自动消失,你可以进行以下哪项操作( )
A.先逆时针旋转90°,再向左平移 B.先顺时针旋转90°,再向左平移
C.先逆时针旋转90°,再向右平移 D.先顺时针旋转90°,再向右平移
12. (2020·沈阳市第一一一中学初一期中)如图,直线,,,则______.
13. (2020·沈阳市第二十三中学初一期中)如图,将一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=35°,则∠2=______.
14. (2020·北京初三专题练习)如图,等腰直角三角板的顶点A,C分别在直线a,b上,若a∥b,∠1=35°,则∠2的度数为________。
15. (2019·浙江初一期中)如图,若,则、、之间的关系为______.
16. (2019·惠安县科山中学初二月考)用反证法证明 “在△ABC中,如果∠B≠∠C,那么AB≠AC”,第一步应假设____________ .
17. (2019·四川初一期末)如图,在△ABC中,∠B=90°,AB=10.将△ABC沿着BC的方向平移至△DEF,若平移的距离是3,则图中阴影部分的面积为________.
18. (2020·沈阳市第二十三中学初一期中)推理填空:
已知:如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
证明:∵EF∥AD,( )
∴∠2= . ( )
∵∠1=∠2,( )
∴∠1=∠3.( )
∴AB∥DG.( )
∴∠BAC+ =180°( )
又∵∠BAC=70°,( )
∴∠AGD= .
19. (2019·湖北初一期中)如图,D,E为△ABC边AB上两点,F,H分别在AC,BC上,∠1+∠2=180°
(1)求证:EF∥DH;
(2)若∠ACB=90°,∠DHB=25°,求∠EFC的度数.
20. (2020·沈阳市第一一一中学初一期中)已知△ABC,∠ACB=90°.
(1)如图1,CD⊥AB于点D,AC=5cm,BC=12cm,AB=13cm,求点C到AB的距离;
(2)如图2,x 轴⊥y轴 , DM⊥y轴,若∠AOG=50°,求∠CEF的度数;
(3)如图3,x 轴⊥y轴,DM⊥y轴,旋转△ABC,使∠C的顶点C在直线DM与x轴之间,N为线段AO上一点,E为BC与DM的交点,F为AB与DM的交点,且∠NEC+∠CEF=180°,下列两个结论:①NEF﹣∠AOG为定值;②NEF/∠AOG为定值,其中只有一个是正确的,请你判断出正确的结论,并求其值.
答案
1. (2020·辽宁初二期末)下列命题中的假命题是( )
A.两直线平行,内错角相等 B.同位角相等,两直线平行
C.两直线平行,同旁内角相等 D.平行于同一条直线的两直线平行
【答案】C
【解析】
A、两直线平行,内错角相等,所以A选项为真命题;
B、同位角相等,两直线平行,所以B选项为真命题;
C、两直线平行,同旁内角互补角,所以C选项为假命题;
D、平行于同一条直线的两直线平行,所以D选项为真命题.
故选C.
【点睛】
本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 有些命题的正确性是用推理证实的,这样的真命题叫做定理.
2. (2020·上海初三专题练习)如图,直线l1∥l2,如果∠1=30°,∠2=50°,那么∠3=( )
A.20° B.80° C.90° D.100°
【答案】B
【解析】
解:过∠3的顶点作l1的平行线m,
∴∠1=∠4,
∵l1∥l2
∴m∥l2,
∴∠2=∠5
∴∠3=∠4+∠5=∠1+∠2=80°
故选:B.
【点睛】
本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.
3. (2020·沈阳市第二十三中学初一期中)如图,将三角形的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为( )
A.10° B.15° C.20° D.25°
【答案】D
【解析】
∵AB∥CD, ∴∠3=∠1=65°, ∴∠2=180°﹣∠3﹣90°=180°﹣65°﹣90°=25°.
4. (2020·北京初三专题练习)如图,AB∥CD,DA⊥CE于点A.若∠D=35°,则∠EAB的度数为( )
A.35° B.45° C.55° D.65°
【答案】C
【解析】
∵AB∥CD,
∴∠BAD=∠D=35°,
∵DA⊥CE,
∴∠DAE=90°,
∴∠EAB=55°.
故选:C.
【点睛】
本题主要考查了平行线的性质以及垂线的定义,解题时注意:两直线平行,内错角相等.
5. (2020·北京初三专题练习)如图,直线,直线EF分别与AB,CD交于点E,F,EG平分,交CD于点G,若,则的度数是( )
A.60° B.55° C.50° D.45°
【答案】B
【解析】
,
,
,
,
,
,
,
故选.
【点睛】
本题主要考查了平行线的性质的应用,角平分线的应用,证出是解题关键.
6. (2020·北京初三专题练习)如图,将一张矩形纸片折叠,若∠1=80°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
【答案】A
【解析】
如图,
∵a∥b,
∴∠1=∠3=80°,
由翻折不变性可知:∠2=∠4= QUOTE EMBED Equation.DSMT4 (180°﹣80°)=50°,
故选A.
【点睛】
本题考查平行线的性质,解题的关键是熟练掌握基本知识.
7. (2020·全国初三专题练习)如图,要修建一条公路,从A村沿北偏东75°方向到B村,从B村沿北偏西25°方向到C村.若要保持公路CE与AB的方向一致,则∠ECB的度数为( )
A.80° B.90° C.100° D.105°
【答案】A
【解析】
解:由题意可得:AN∥FB,EC∥BD,
∴∠NAB=∠FBD=75°,
∵∠CBF=25°,
∴∠CBD=100°,
则∠ECB=180°-100°=80°.
故选:A.
【点睛】
本题考查方向角,正确得出平行线,利用平行线的性质是解题关键.
8. (2019·浙江初二月考)下列句子属于命题的是( ).
A.正数大于一切负数吗? B.钝角大于直角
C.将开平方 D.作线段的中点
【答案】B
【解析】
A 、正数大于一切负数吗?为疑问句,它不是命题,所以A选项错误;
B 、钝角大于直角是命题,所以B选项正确;
C、将16开平方为陈述句,它不是命题,所以C选项错误;
D 、作线段AB的中点为陈述句,它不是命题,所以D选项错误,
故选 B .
9. (2020·四川初二月考)下列命题中,其逆命题是假命题的是( ?)
A.若ab=1,则a与b互为倒数 B.如果|a|=|b|,那么a2=b2
C.等腰三角形的两个底角相等 D.若两个数的差为正数,则这两个数都为正数
【答案】D
【解析】
解:A、若a与b互为倒数,则ab=1;故A的逆命题是真命题;
B、如果a2=b2,则|a|=|b|;故B的逆命题是真命题;
C、如果三角形的两个底角相等,那么这个三角形是等腰三角形;故C的逆命题是真命题;
D、若两个数是正数,那么这两个数的差为正数;故D的逆命题是假命题;
故选择:D.
【点睛】
此题考查了命题与逆命题的关系.解题的关键是找到各命题的逆命题,再证明正误即可.
10. (2019·上海市南洋模范中学初二月考)下列定理中,没有逆定理的是( )
A.两直线平行,同旁内角互补; B.两个全等三角形的对应角相等
C.直角三角形的两个锐角互余; D.两内角相等的三角形是等腰三角形
【答案】B
【解析】
A.其逆命题是“同旁内角互补,两直线平行”,正确,所以有逆定理;
B.其逆命题是“对应角相等的三角形是全等三角形”,错误,所以没有逆定理;
C.其逆命题是“两个锐角互余的三角形是直角三角形”,正确,所以有逆定理;
D.其逆命题是“等腰三角形的两个内角相等”,正确,所以有逆定理.
故选B.
【点睛】
本题考查了命题与定理的区别,正确的命题叫定理.
11. (2019·福建初一期末)在俄罗斯方块游戏中,若某行被小方格块填满,则该行中的所有小方格会自动消失.现在游戏
机屏幕下面三行已拼成如图所示的图案,屏幕上方又出现一小方格块正向下运动,为了使屏幕下面三行中的小方格都自动消失,你可以进行以下哪项操作( )
A.先逆时针旋转90°,再向左平移 B.先顺时针旋转90°,再向左平移
C.先逆时针旋转90°,再向右平移 D.先顺时针旋转90°,再向右平移
【答案】A
【解析】
屏幕上方又出现一小方格块正向下运动,为了使屏幕下面三行中的小方格都自动消失,可以先逆时针旋转90°,再向左平移.
故选A.
12. (2020·沈阳市第一一一中学初一期中)如图,直线,,,则______.
【答案】142°.
【解析】
如图延长直接交l1,其夹角为∠3,
∵∠α=∠β,
∴∠3=∠1=38°
∵l1∥l2,
∴∠2=180°-∠3=142°.
【点睛】
此题主要考查平行线的性质,解题的关键是根据题意作出辅助线.
13. (2020·沈阳市第二十三中学初一期中)如图,将一个含有30°角的直角三角形的两个顶点放在一个矩形的对边上,若∠1=35°,则∠2=______.
【答案】125°
【解析】
解:如图,
∵∠1+∠3+90°=180°,∠1=35°,
∴∠3=90°-35°=55°.
∵矩形对边平行,
∴∠2+∠3=180°,
∴∠2=180°-∠3=125°.
故答案为:125°.
【点睛】
本题考查了平行线的性质以及平角定义,解题关键是根据两直线平行,同旁内角互补解答问题.
14. (2020·北京初三专题练习)如图,等腰直角三角板的顶点A,C分别在直线a,b上,若a∥b,∠1=35°,则∠2的度数为________。
【答案】10°
【解析】
解:如图,
由题意可知
又
故答案是10°
【点睛】
本题考察两直线平行,内错角相等,灵活运用等腰直角三角形中的角是解题的关键.
15. (2019·浙江初一期中)如图,若,则、、之间的关系为______.
【答案】
【解析】
过点E作EF∥AB,如图所示.
∵AB∥CD,EF∥AB,
∴EF∥CD∥AB,
∴∠α+∠AEF=180°,∠γ=∠CEF.
又∵∠AEF+∠CEF=∠β,
∴∠α+∠β?∠γ=180°.
故答案为∠α+∠β?∠γ=180°.
【点睛】
考查平行公理以及平行线的性质,掌握平行线的性质是解题的关键.
16. (2019·惠安县科山中学初二月考)用反证法证明 “在△ABC中,如果∠B≠∠C,那么AB≠AC”,第一步应假设____________ .
【答案】AB=AC
【解析】
解:用反证法证明命题“在△ABC中,∠B≠∠C,那么AB≠AC”的过程中,
第一步应是假设AB=AC.
故答案为:AB=AC.
【点睛】
本题结合角的比较考查反证法,解此题关键要懂得反证法的意义及步骤.
反证法的步骤是:(1)假设结论不成立;(2)从假设出发推出矛盾;(3)假设不成立,则结论成立.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.
17. (2019·四川初一期末)如图,在△ABC中,∠B=90°,AB=10.将△ABC沿着BC的方向平移至△DEF,若平移的距离是3,则图中阴影部分的面积为________.
【答案】30
【解析】
解:∵直角△ABC沿BC边平移3个单位得到直角△DEF,∴AC=DF,AD=CF=3,∴四边形ACFD为平行四边形,∴S平行四边形ACFD=CF?AB=3×10=30,即阴影部分的面积为30.故答案为:30.
点睛:本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.也考查了平行四边形的面积公式.
18. (2020·沈阳市第二十三中学初一期中)推理填空:
已知:如图,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
证明:∵EF∥AD,( )
∴∠2= . ( )
∵∠1=∠2,( )
∴∠1=∠3.( )
∴AB∥DG.( )
∴∠BAC+ =180°( )
又∵∠BAC=70°,( )
∴∠AGD= .
【答案】见解析
【解析】
解:(1)∵EF∥AD,(已知)
∴∠2=∠3.(两直线平行,同位角相等)
又∵∠1=∠2,(已知)
∴∠1=∠3.(等量代换)
∴AB∥DG.(内错角相等,两直线平行)
∴∠BAC+∠AGD=180°.(两直线平行,同旁内角互补)
又∵∠BAC=70°,(已知)
∴∠AGD=110°.
【点睛】
本题考查了平行线的判定与性质;熟练掌握平行线的判定与性质是解答关键.
19. (2019·湖北初一期中)如图,D,E为△ABC边AB上两点,F,H分别在AC,BC上,∠1+∠2=180°
(1)求证:EF∥DH;
(2)若∠ACB=90°,∠DHB=25°,求∠EFC的度数.
【答案】(1)见解析;(2)∠EFC=115°.
【解析】
(1)证明:∵∠1+∠2=180°,∠ADH+∠2=180°,
∴∠1=∠ADH,
∴EF∥DH;
(2)解:过点C作CG∥DH,交AB于G,如图所示:
则∠GCB=∠DHB=25°,
∴∠ACG=∠ACB﹣∠GCB=90°﹣25°=65°,
由(1)得:EF∥DH,
∴CG∥EF,
∴∠EFC+∠ACG=180°,
∴∠EFC=180°﹣∠ACG=180°﹣65°=115°.
【点睛】
本题考查了平行线的判定与性质,熟练掌握平行线的性质是解题的关键.
20. (2020·沈阳市第一一一中学初一期中)已知△ABC,∠ACB=90°.
(1)如图1,CD⊥AB于点D,AC=5cm,BC=12cm,AB=13cm,求点C到AB的距离;
(2)如图2,x 轴⊥y轴 , DM⊥y轴,若∠AOG=50°,求∠CEF的度数;
(3)如图3,x 轴⊥y轴,DM⊥y轴,旋转△ABC,使∠C的顶点C在直线DM与x轴之间,N为线段AO上一点,E为BC与DM的交点,F为AB与DM的交点,且∠NEC+∠CEF=180°,下列两个结论:①NEF﹣∠AOG为定值;②NEF/∠AOG为定值,其中只有一个是正确的,请你判断出正确的结论,并求其值.
【答案】(1);(2)∠CEF=140°;(3),是定值
【解析】
解:(1)∵AC⊥BC,BC=12cm,
∴AC
∴
∴
∴点C到AB的距离为
故答案为:
(2)∵∠AOG=50°,
∴∠POD=50°,
∴∠COD=40°,
∴∠CQO=50°,
∴∠DQE=50°,
∴∠CED=40°,
∴∠CEF=140°;
(3)为定值.理由如下:
作CP∥x轴,如图3,
∵CP∥DM∥x轴,
∴∠AOG=∠1,∠2+∠CEF=180°,
而∠NEC+∠CEF=180°,
∴∠2=∠NEC,
∵∠1+∠2=90°,
∠NEF+2∠2=180°,
∴∠NEF=2∠1=2∠AOG,
∴,是定值.
【点睛】
此题考查了平行线的判定与性质:平行线于同一条直线的两直线平行;两直线平行,同位角相等;两直线平行,同旁内角互补.
