1.4.3 整式的乘法课件
图片预览






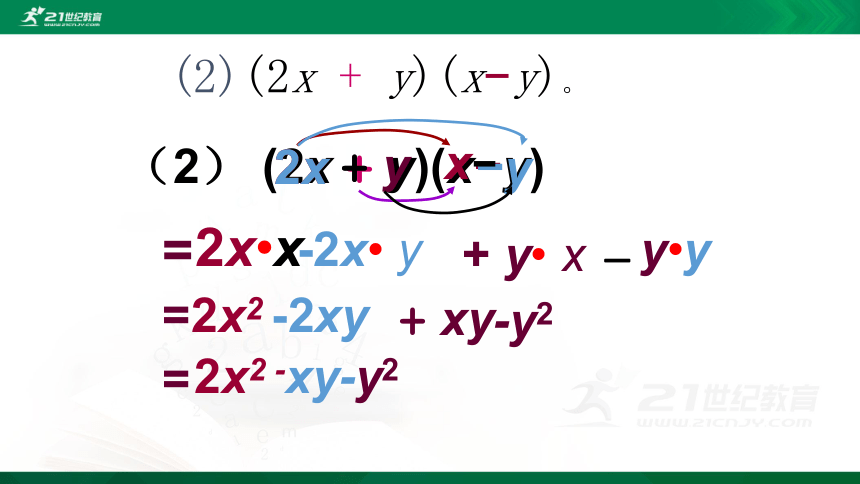
文档简介
(共19张PPT)
数学北师大版
九年级
1.4整式的乘法
第3课时多项式乘多项式
am
bn
an
bm
问题:如图,为了扩大街心花园的绿地面积,把一块原长a米、宽m米的长方形绿地,增长了b米,加宽了n米,你能用几种方法求出扩大后的绿地面积?
新知导入
1、(a+b)(m+n)
a
b
m
n
am
an
bm
bn
4、(am+an+bm+bn)
即 (a+b)(m+n)=am+an+bm+bn
2、a(m+n)+b(m+n)
3、m(a+b)+n(a+b)
(a+b)(m+n)
=a(m+n)+b(m+n)
=m(a+b)+n(a+b)
=(am+an+bm+bn)
故
(a+b)(m+n)
这怎么会得到呢?
=m(a+b)+n(a+b)
只要把(a+b)看成一个整体便可用单项式乘以多项式法则了,
同理可得
(a+b)(m+n)
=a(m+n)+b(m+n)
=(am+an+bm+bn)
即 (a+b)(m+n)=am+an+bm+bn
多项式的乘法法则
+an
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+bm
+bn
多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.
新知讲解
例题解析
【例1】计算:
(1)(1?x)(0.6?x);
解:
(1) (1?x)(0.6?x)
-
x
-0.6 ? x
+
=
0.6-1.6x+x2
x? x
=0.6
最后的结果要合并同类项.
两项相乘时,先定符号
例题解析
(2)(2x + y)(x?y)。
(2) (2x + y)(x?y)
=
2x
x
2x?x
2x
?y
-2x? y
+ y
+ y? x
+
?
-
y?y
=
2x2
-2xy
+ xy
-y2
=
2x2 -xy-y2
(1) (-2x+3y)(x2-xy+2y2)
解:原式
=-2x3 +2x2y-4xy2+3x2y-3xy2+6y3
=-2x3 +5x2y-7xy2+6y3
在没有合并同类项之前,两个多项式相乘展开后的项数应是这两个多项式项数之积。
例2
分析:前一括号是-2x和+3y这二项,后一括号是
x2 -xy 和+2y2这三项
先化简,再求值;
其中x=2,y=-1
(2)
解:原式=
当x=2,y=-1时,
(3)x(1-x)+(x-2)(x+1).
随堂练习
例3若(x+ay)(x+by)=x2-2xy-5y2,求(a+b)·ab
解:∵(x+ay)(x+by)=x2-2xy-5y2,
∴x2+bxy+axy+aby2=x2-2xy-5y2,
∴x2+bxy+axy+aby2=x2-2xy-5y2,
∴a+b=-2
,ab=-5
∴ (a+b)·ab =
(-2)×(-5)
=10
∴x2+(a+b)xy++aby2=x2-2xy-5y2,
提高训练
1,若m,n是整数,且有
(mx-3y)(3x+2y)=6x2-nxy-6y2
求m,n的值
解: (mx-3y)(3x+2y)
=3mx2+2mxy-9xy-6y2
= 3mx2+(2m-9) xy-6y2
比较系数得:
3m=6
2m-9=-n
解得: m=2
n=5
2、在长为3a+2,宽为2b+3的长方形铁片上,挖去长为b+1,宽为a-1的小长方形铁片,求剩下部分的面积。
解:(3a+2)(2b+3)-(b+1)(a-1)
=6ab+9a+4b+6-ab+b-a+1
=5ab+8a+5b+7
本课小结:多项式的乘法法则
+an
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+bm
+bn
多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.
课外作业
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
数学北师大版
九年级
1.4整式的乘法
第3课时多项式乘多项式
am
bn
an
bm
问题:如图,为了扩大街心花园的绿地面积,把一块原长a米、宽m米的长方形绿地,增长了b米,加宽了n米,你能用几种方法求出扩大后的绿地面积?
新知导入
1、(a+b)(m+n)
a
b
m
n
am
an
bm
bn
4、(am+an+bm+bn)
即 (a+b)(m+n)=am+an+bm+bn
2、a(m+n)+b(m+n)
3、m(a+b)+n(a+b)
(a+b)(m+n)
=a(m+n)+b(m+n)
=m(a+b)+n(a+b)
=(am+an+bm+bn)
故
(a+b)(m+n)
这怎么会得到呢?
=m(a+b)+n(a+b)
只要把(a+b)看成一个整体便可用单项式乘以多项式法则了,
同理可得
(a+b)(m+n)
=a(m+n)+b(m+n)
=(am+an+bm+bn)
即 (a+b)(m+n)=am+an+bm+bn
多项式的乘法法则
+an
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+bm
+bn
多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.
新知讲解
例题解析
【例1】计算:
(1)(1?x)(0.6?x);
解:
(1) (1?x)(0.6?x)
-
x
-0.6 ? x
+
=
0.6-1.6x+x2
x? x
=0.6
最后的结果要合并同类项.
两项相乘时,先定符号
例题解析
(2)(2x + y)(x?y)。
(2) (2x + y)(x?y)
=
2x
x
2x?x
2x
?y
-2x? y
+ y
+ y? x
+
?
-
y?y
=
2x2
-2xy
+ xy
-y2
=
2x2 -xy-y2
(1) (-2x+3y)(x2-xy+2y2)
解:原式
=-2x3 +2x2y-4xy2+3x2y-3xy2+6y3
=-2x3 +5x2y-7xy2+6y3
在没有合并同类项之前,两个多项式相乘展开后的项数应是这两个多项式项数之积。
例2
分析:前一括号是-2x和+3y这二项,后一括号是
x2 -xy 和+2y2这三项
先化简,再求值;
其中x=2,y=-1
(2)
解:原式=
当x=2,y=-1时,
(3)x(1-x)+(x-2)(x+1).
随堂练习
例3若(x+ay)(x+by)=x2-2xy-5y2,求(a+b)·ab
解:∵(x+ay)(x+by)=x2-2xy-5y2,
∴x2+bxy+axy+aby2=x2-2xy-5y2,
∴x2+bxy+axy+aby2=x2-2xy-5y2,
∴a+b=-2
,ab=-5
∴ (a+b)·ab =
(-2)×(-5)
=10
∴x2+(a+b)xy++aby2=x2-2xy-5y2,
提高训练
1,若m,n是整数,且有
(mx-3y)(3x+2y)=6x2-nxy-6y2
求m,n的值
解: (mx-3y)(3x+2y)
=3mx2+2mxy-9xy-6y2
= 3mx2+(2m-9) xy-6y2
比较系数得:
3m=6
2m-9=-n
解得: m=2
n=5
2、在长为3a+2,宽为2b+3的长方形铁片上,挖去长为b+1,宽为a-1的小长方形铁片,求剩下部分的面积。
解:(3a+2)(2b+3)-(b+1)(a-1)
=6ab+9a+4b+6-ab+b-a+1
=5ab+8a+5b+7
本课小结:多项式的乘法法则
+an
1
2
3
4
(a+b)(m+n)
=
am
1
2
3
4
+bm
+bn
多项式与多项式相乘, 先用一个多项式的每一项乘以另一个多项式的每一项, 再把所得的积相加.
课外作业
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
