人教版九年级数学上册 第23章 旋转数学活动综合专题讲义学案(无答案)
文档属性
| 名称 | 人教版九年级数学上册 第23章 旋转数学活动综合专题讲义学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 152.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-22 00:00:00 | ||
图片预览



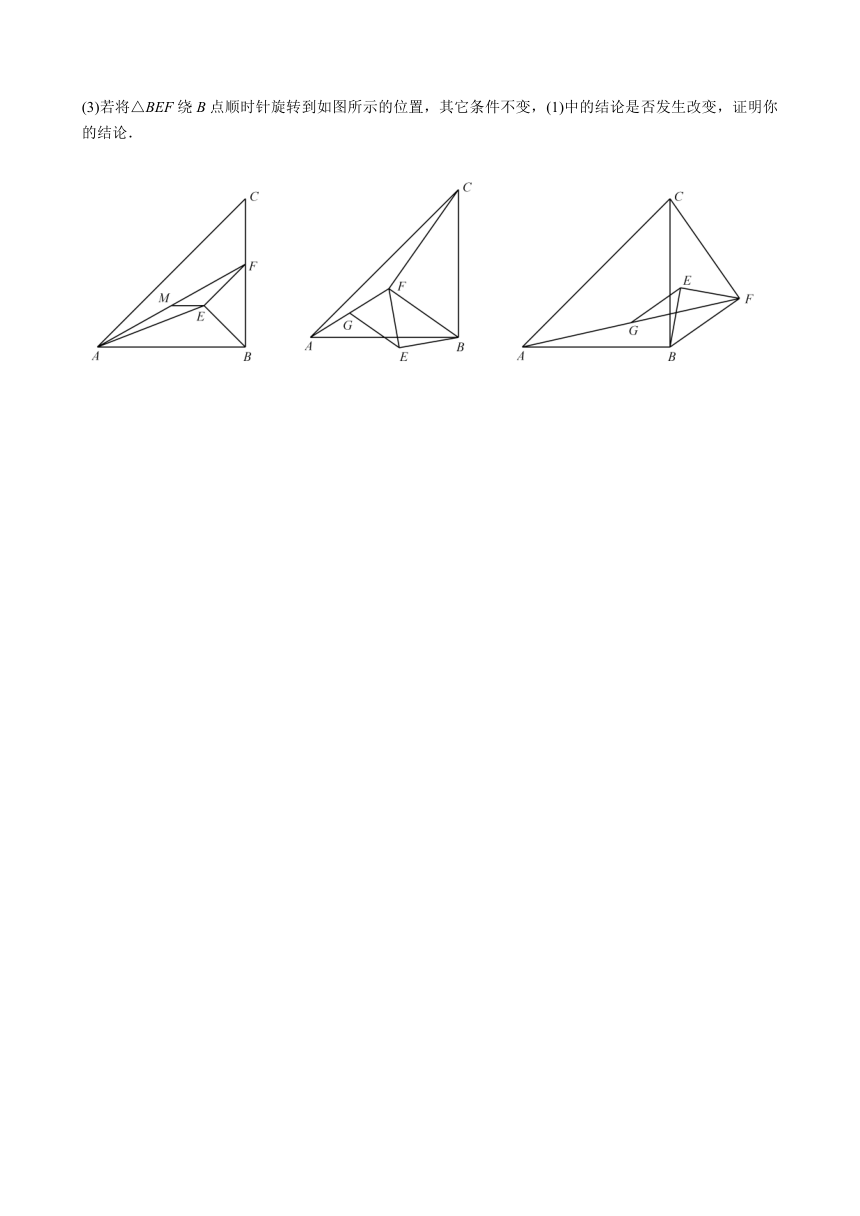
文档简介
第6讲 旋转综合(二)
知识目标:
目标一:掌握等腰直角三角形———90°手拉手
目标二:掌握等腰直角三角形———45°脚拉脚(逆序)
目标三:掌握等腰直角三角形———45°脚拉脚(顺序)
模块一 旋转三大模型
模型一 等腰直角三角形———90°手拉手
△ABC和△DBE为等腰三角形,∠ABC=∠DBE=90°
例1.(1)如图,已知△ABC为等腰直角三角形,DE∥BC,F、G、H三点分别为BE、CD、DE的中点,试求∠HFG的度数.
(2)若将(1)中的△ADE绕A点顺时针旋转一个度数,如图所示,其它条件不变,问∠HFG的度数是否变化?
【练】已知△ABC与△ADE为等腰直角三角形,∠BAC=∠DAE=90°,F、G、H三点分别为BD、CE、BC的中点,求证:HG=HF,HG⊥HF.
例2.(1)已知△ABC与△CDE为等腰直角三角形,∠ACB=∠CDE=90°,M是BE的中点,点D在线段CB上,探索:DM与AE的关系?
(2)若将△CDE绕C点逆时针旋转到如图所示的位置,其它条件不变,(1)中的结论是否发生改变,证明你的结论.
(3)若将△CDE绕C点顺时针旋转到如图所示的位置,其它条件不变,(1)中的结论是否发生改变,证明你的结论.
【练】(1)已知△ABC与△BEF为等腰直角三角形,∠ABC=∠BEF=90°,M是AF的中点,探索:CF与ME的关系?
(2)若将△BEF绕B点逆时针旋转到如图所示的位置,其它条件不变,(1)中的结论是否发生改变,证明你的结论.
(3)若将△BEF绕B点顺时针旋转到如图所示的位置,其它条件不变,(1)中的结论是否发生改变,证明你的结论.
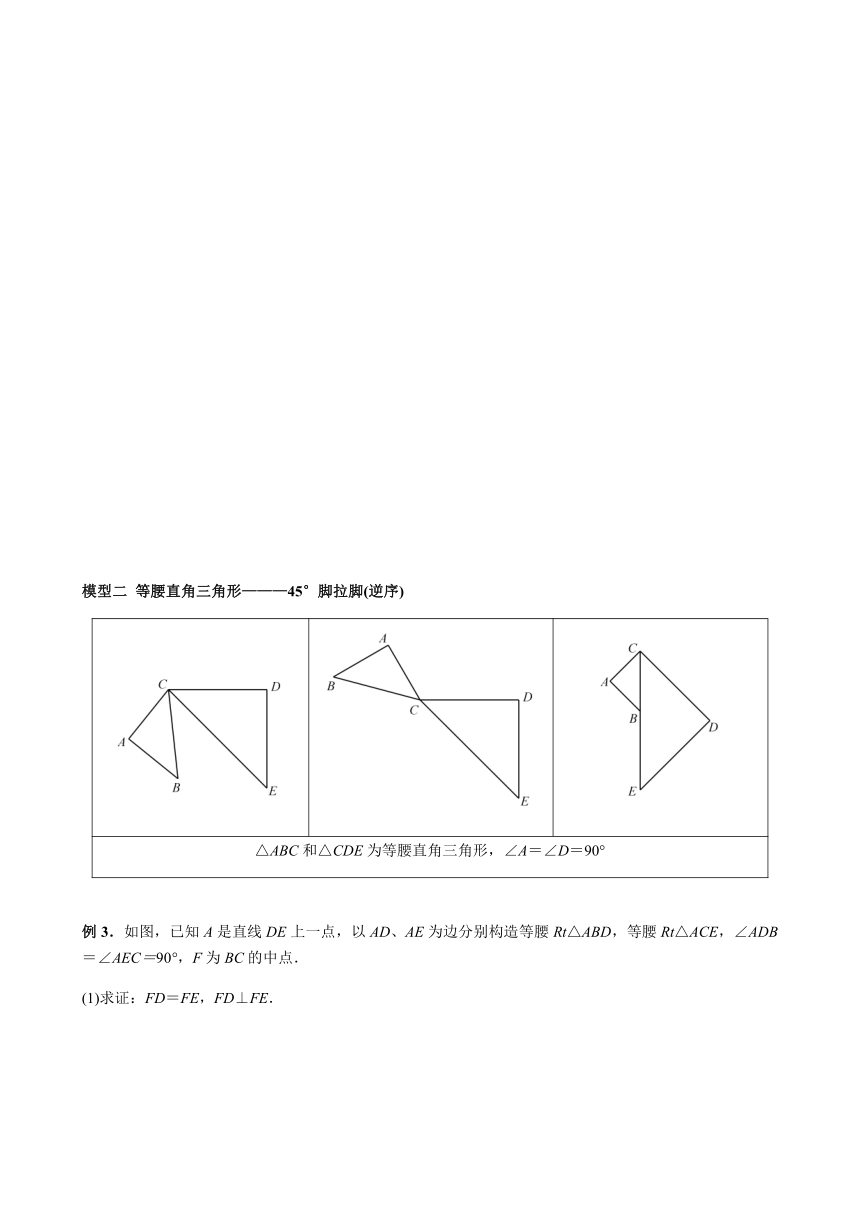
模型二 等腰直角三角形———45°脚拉脚(逆序)
△ABC和△CDE为等腰直角三角形,∠A=∠D=90°
例3.如图,已知A是直线DE上一点,以AD、AE为边分别构造等腰Rt△ABD,等腰Rt△ACE,∠ADB=∠AEC=90°,F为BC的中点.
(1)求证:FD=FE,FD⊥FE.
(2)若将△ADB绕A点逆时针旋转到如图所示的位置,其它条件不变,(1)中的结论是否仍然成立?
(3)若将△ADB绕A点顺时针旋转到如图所示的位置,其它条件不变,(1)中的结论是否发生改变,证明你的结论.
(4)若将(3)中的△ADB继续绕A点顺时针旋转到如图所示的位置,其它条件不变,(1)中的结论是否仍然成立?证明你的结论.
例4.已知△ABC中,AB=AC,N为BC的中点,△DBE中,DB=DE,M为BE的中点,∠ABC=∠DBE=a,连AD,P为AD的中点,连PM、PN.
(1)如图1,当BE与BA重合时,PM和PN有什么数量关系?先回答,并加以证明.
(2)如图2,若将图1中的△BDE绕B点逆时针旋转(0<<a),其它条件不变,问(1)中的结论是否仍然成立?先回答,再说明理由.
【练】已知△ABC,以AB、AC为腰向△ABC外作等腰△ABE和等腰△ACF,∠ABE=∠ACF,G为BC的中点,M、N分别为底边AE、底边AF的中点,求证:GM=GN.
模型三 等腰直角三角形———45°脚拉脚(顺序)
△ABC和△CDE为等腰直角三角形,∠A=∠D=90°
例5.(1)已知△ABC与△ADE为等腰直角三角形,∠ABC=∠ADE=90°,直线BD与直线CE交于点F,求∠F的度数,以及BD和CE的数量关系.
(2)若将(1)中的△ADE绕A点逆时针旋转到如图所示的位置,其它条件不变,求∠F的度数,以及BD和CE的数量关系.
(3)若将(1)中的△ADE绕A点逆时针旋转到如图所示的位置,其它条件不变,求∠BFC的度数,以及BD和CE的数量关系.
(4)若将(1)中的△ADE绕A点逆时针旋转到如图所示的位置,其它条件不变,求∠BFC的度数,以及BD和CE的数量关系.
(5)若将(1)中的△ADE绕A点逆时针旋转到如图所示的位置,其它条件不变,求∠BFC的度数,以及BD和CE的数量关系.
模块二 旋转综合运用
例6.如图1,Rt△ABC中,∠C=90°,∠A=30°,BC=,P为AC边上一动点,PC=t,以点P为中心,将△ABC逆时针旋转90°,得到△DEF,DE交AC于点G.
(1)用含t的式子填空:DP= ,AG= .
(2)如图2,当点F在AB上时,求证:PG=PC.
(3)如图2,当点P为DP的中点时,求AG:PG的值.
图1 图2 图3
例7.在△ABC和△CDE中,AB=AC,CE=DE,∠BAC=∠CED=90°.
(1)如图1,N为BD的中点,连接AN、EN.求证:①AN=EN.②AN⊥EN.
(2)如图2,M为CD的中点,连接AM、BE交于点F.求证:①BE=AM.②∠MFE=45°.
(3)如图3,在(2)的条件下,连接DF,猜想DF、EF、MF之间的数量关系,并证明你的结论.
图1 图2 图3
第6讲 旋转综合(二)课后作业
1.如图,△ACB、△AED都为等腰直角三角形,∠ACB=∠AED=90°,点D在AB上,连CE,M、N分别为BD、CE的中点.
(1)如图1,当点D在线段AB上时,求证:MN⊥CE;
(2)如图2,将(1)中的△AED绕A点逆时针旋转30°,求证:CE=2MN;
(3)当△AED绕A点逆时针旋转过程中,试判断是否为定值,若为定值,求出此值,若不是,求出变化范围.
图1 图2
2.
(1)如图1,∠BAC=∠BEC=90,且BE=CE,求证:AE平分∠BAC;
(2)如图2,四边形ABCD为菱形,E、F分别在对角线AC、边AB的延长线上,试探究:当∠BAD与∠DFE满足什么关系时,使得DF=EF成立?并证明你的结论;
(3)在(1)的条件下,若AE=4,请求出线段BE的取值范围.
图1 图2
同课章节目录
