沪科版七年级数学下册 第10章 相交线与平行线 单元测试题(无答案)
文档属性
| 名称 | 沪科版七年级数学下册 第10章 相交线与平行线 单元测试题(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 79.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-21 00:00:00 | ||
图片预览


文档简介
沪科版七年级数学下册 第10章 相交线与平行线 单元测试题
一、选择题
1.三条直线相交,交点最多有( )
A.1个 B.2个 C.3个 D.4个
2.如图,现要从村庄A修建一条连接公路PQ的最短小路,过点A作AH⊥PQ于点H,沿AH修建公路,这样做的理由是( )
A.两点之间,线段最短
B.垂线段最短
C.过一点可以作无数条直线
D.两点确定一条直线
3.如图,直线a∥b,∠1=32°,∠2=45°,则∠3的度数是( )
A.77° B.97° C.103° D.113°
4.如图,直线a,b被直线m所截,若a∥b,∠2=62°,则∠1=( )
A.62° B.108° C.118° D.128°
5.如图,直线AB∥CD,CE平分∠ACD,交AB于点E,∠ACE=20°,点F在AC的延长线上,则∠BAF的度数为( )
A.20° B.30° C.40° D.50°
6.如图,AB∥CD,∠B=2∠D,∠E=22°,则∠D的度数为( )
A.22° B.44° C.68° D.30°
7.若P,Q是直线AB外不重合的两点,则下列说法不正确的是( )
A.直线PQ可能与直线AB垂直
B.直线PQ可能与直线AB平行
C.过点P的直线一定能与直线AB相交
D.过点Q只能画出一条直线与直线AB平行
8.如图,△ABC中,CD是AB边上的高,CM是AB边上的中线,点C到边AB所在直线的距离是( )
A.线段CA的长度 B.线段CM的长度
C.线段CD的长度 D.线段CB的长度
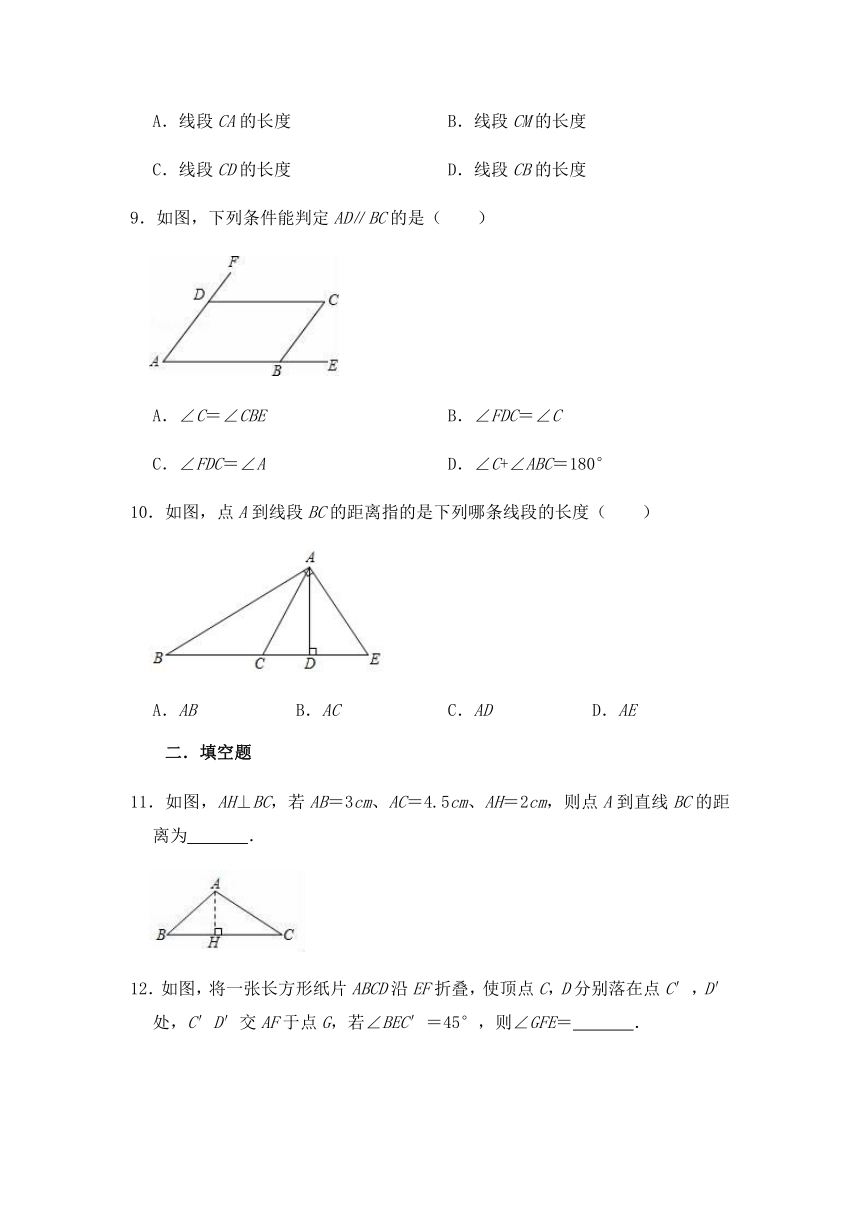
9.如图,下列条件能判定AD∥BC的是( )
A.∠C=∠CBE B.∠FDC=∠C
C.∠FDC=∠A D.∠C+∠ABC=180°
10.如图,点A到线段BC的距离指的是下列哪条线段的长度( )
A.AB B.AC C.AD D.AE
二.填空题
11.如图,AH⊥BC,若AB=3cm、AC=4.5cm、AH=2cm,则点A到直线BC的距离为 .
12.如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′D′交AF于点G,若∠BEC′=45°,则∠GFE= .
13.如图,一个含有30°角的直角三角尺的两个顶点放在一个长方形的对边上.若∠1=30°,则∠2= °.?
14.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是 .?
15.如图,AB∥CD,且AC⊥BD,垂足为E,∠BAC=α°,则∠BDC= °(用含α的式子表示).
16.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上如果∠2=35°,那么∠1的度数是 度.
三.解答题
17.如图,将直角三角板的直角顶点放在一条直线上,∠1为任意钝角,则∠1﹣∠2= °.
18.如图已知AB,CD,EF三直线相交于点O,且OE⊥AB,∠COE=20°,OG平分∠BOD,求∠BOG的度数.
19.已知:如图,∠1+∠2=180°,∠A=∠D.求证:AB∥CD.(在每步证明过程后面注明理由)
20.如图,OA⊥OB,引射线OC(点C在∠AOB外),若∠BOC=α(0°<α<90°),OD平分∠BOC,OE平分∠AOD.
(1)若α=40°,请依题意补全图形,并求∠BOE的度数;
(2)请根据∠BOC=α,求出∠BOE的度数(用含α的表示).
21.如图,在四边形ABCD中,CD∥AB,E是AD中点,CE交BA延长线于点F.
(1)证明:CD=AF;
(2)若BE⊥CF,证明:BC=BF.
22.探究题:
(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由;
(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论;
(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.
一、选择题
1.三条直线相交,交点最多有( )
A.1个 B.2个 C.3个 D.4个
2.如图,现要从村庄A修建一条连接公路PQ的最短小路,过点A作AH⊥PQ于点H,沿AH修建公路,这样做的理由是( )
A.两点之间,线段最短
B.垂线段最短
C.过一点可以作无数条直线
D.两点确定一条直线
3.如图,直线a∥b,∠1=32°,∠2=45°,则∠3的度数是( )
A.77° B.97° C.103° D.113°
4.如图,直线a,b被直线m所截,若a∥b,∠2=62°,则∠1=( )
A.62° B.108° C.118° D.128°
5.如图,直线AB∥CD,CE平分∠ACD,交AB于点E,∠ACE=20°,点F在AC的延长线上,则∠BAF的度数为( )
A.20° B.30° C.40° D.50°
6.如图,AB∥CD,∠B=2∠D,∠E=22°,则∠D的度数为( )
A.22° B.44° C.68° D.30°
7.若P,Q是直线AB外不重合的两点,则下列说法不正确的是( )
A.直线PQ可能与直线AB垂直
B.直线PQ可能与直线AB平行
C.过点P的直线一定能与直线AB相交
D.过点Q只能画出一条直线与直线AB平行
8.如图,△ABC中,CD是AB边上的高,CM是AB边上的中线,点C到边AB所在直线的距离是( )
A.线段CA的长度 B.线段CM的长度
C.线段CD的长度 D.线段CB的长度
9.如图,下列条件能判定AD∥BC的是( )
A.∠C=∠CBE B.∠FDC=∠C
C.∠FDC=∠A D.∠C+∠ABC=180°
10.如图,点A到线段BC的距离指的是下列哪条线段的长度( )
A.AB B.AC C.AD D.AE
二.填空题
11.如图,AH⊥BC,若AB=3cm、AC=4.5cm、AH=2cm,则点A到直线BC的距离为 .
12.如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C′,D′处,C′D′交AF于点G,若∠BEC′=45°,则∠GFE= .
13.如图,一个含有30°角的直角三角尺的两个顶点放在一个长方形的对边上.若∠1=30°,则∠2= °.?
14.在直线AB上任取一点O,过点O作射线OC,OD,使OC⊥OD,当∠AOC=30°时,∠BOD的度数是 .?
15.如图,AB∥CD,且AC⊥BD,垂足为E,∠BAC=α°,则∠BDC= °(用含α的式子表示).
16.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上如果∠2=35°,那么∠1的度数是 度.
三.解答题
17.如图,将直角三角板的直角顶点放在一条直线上,∠1为任意钝角,则∠1﹣∠2= °.
18.如图已知AB,CD,EF三直线相交于点O,且OE⊥AB,∠COE=20°,OG平分∠BOD,求∠BOG的度数.
19.已知:如图,∠1+∠2=180°,∠A=∠D.求证:AB∥CD.(在每步证明过程后面注明理由)
20.如图,OA⊥OB,引射线OC(点C在∠AOB外),若∠BOC=α(0°<α<90°),OD平分∠BOC,OE平分∠AOD.
(1)若α=40°,请依题意补全图形,并求∠BOE的度数;
(2)请根据∠BOC=α,求出∠BOE的度数(用含α的表示).
21.如图,在四边形ABCD中,CD∥AB,E是AD中点,CE交BA延长线于点F.
(1)证明:CD=AF;
(2)若BE⊥CF,证明:BC=BF.
22.探究题:
(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与直线CD有什么位置关系?简要说明理由;
(3)若将点E移至图2的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论;
(4)若将点E移至图3的位置,此时∠B、∠D、∠E之间有什么关系?直接写出结论.
