人教版数学八年级下册18.1.2 平行四边形的判定课件(33张PPT)
文档属性
| 名称 | 人教版数学八年级下册18.1.2 平行四边形的判定课件(33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 685.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-21 22:51:06 | ||
图片预览





文档简介
课件33张PPT。人教版初中数学18.1.2 平行四边形判定情景
引入讲授
新课归纳
总结情景
引入导入
新课课后
作业1.八下数学课本(翻到18.1.2平行四边形的判定)
2.平行四边形的判定导学案(练习本)
3.双色笔(红和黑)
4.刻度尺或三角板。学习工具准备:课前准备平行四边形的定义:
符号语言
∵四边形ABCD是平行四边形
∴ AB//CD,AD//BC温故知新
对边分别 的四边形叫做平行四边形。
性质两组平行平行四边形的对边平行且相等。 平行四边形的对角线互相平分。平行四边
形的性质平行四边形的对角相等。
∵四边形ABCD是平行边形
∴ ∠A=∠ C, ∠ D=∠ B
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD性质定义判定平行四边形学习重点、难点重点:平行四边形判定方法的探究.
难点:平行四边形判定方法的理解和灵活应用.
学习目标1.经历平行四边形判定定理的猜想与证明过程,
体会类比、转化的思想及探究图形判定的一般思路.
2.掌握平行四边形的判定定理,能根据不同条件灵活选取适当的判定定理进行推理论证.
平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形
符号语言
∵AB//CD,AD//BC
∴ .
探究新知1定义是平行四边形的原始的判定方法定义法四边形ABCD是平行四边形
1、平行四边形的两组对边分别相等;(边)
2、平行四边形的两组对角分别相等; (角)
3、平行四边形的对角线互相平分.(对角线)问题:
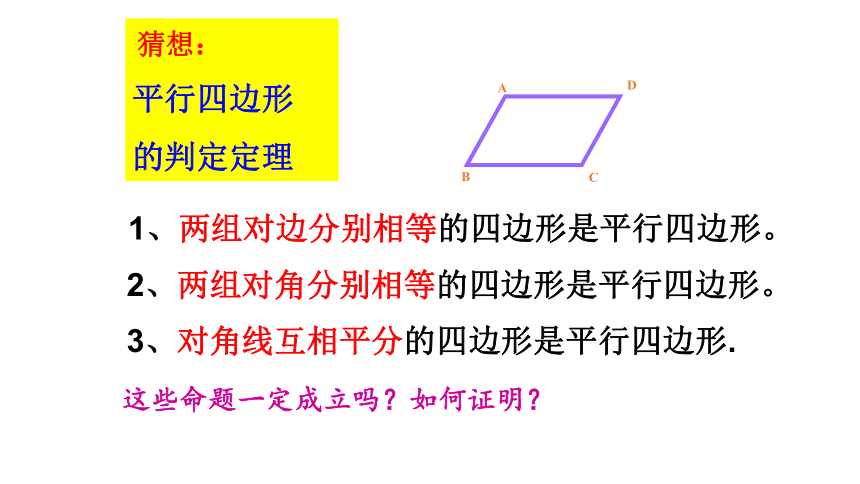
请写出以上命题的逆命题.逆命题: 1、两组对边分别相等的四边形是平行四边形.2、两组对角分别相等的四边形是平行四边形.3、对角线互相平分的四边形是平行四边形.平行四边形的性质:1、两组对边分别相等的四边形是平行四边形。2、两组对角分别相等的四边形是平行四边形。3、对角线互相平分的四边形是平行四边形.
平行四边形
的判定定理猜想:这些命题一定成立吗?如何证明?BDAC 四边形ABCD是平行四边形AB∥ CD,AD ∥ BC△ABC≌△CDA∠BAC=∠DCA,∠ACB=∠CAD(S.S.S)平行四边形(证明角相等)思路:定义法转
化连
接
对
角
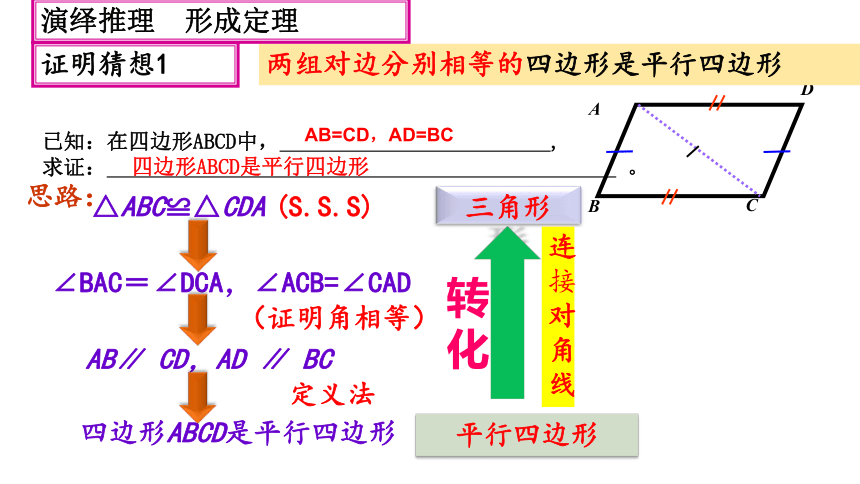
线已知:在四边形ABCD中, ,
求证: 。 AB=CD,AD=BC四边形ABCD是平行四边形两组对边分别相等的四边形是平行四边形证明猜想1 演绎推理 形成定理 证明:连接AC在△ABC和△CDA中∴△ABC≌△CDA(SSS)
∴∠BAC=∠DCA,∠ACB=∠CAD(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
已知:四边形ABCD中,AB=CD,AD=BC
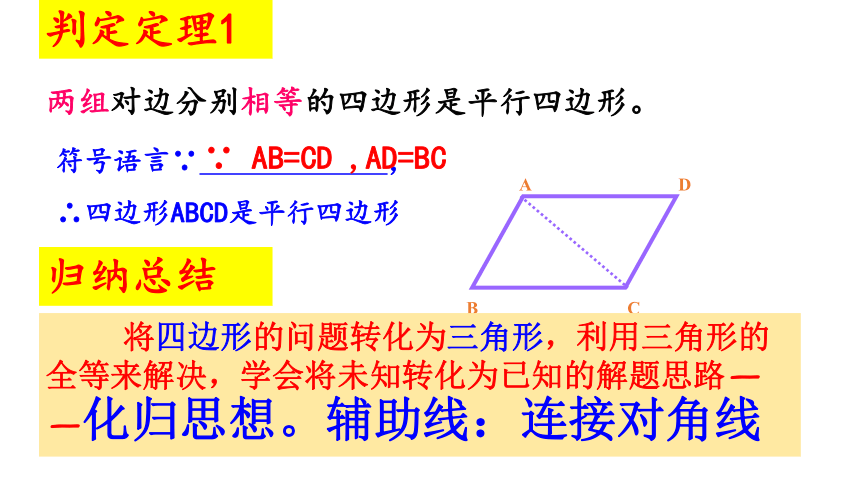
求证:四边形ABCD是平行四边形两组对边分别相等的四边形是平行四边形。判定定理1猜想1两组对边分别相等的四边形是平行四边形。判定定理1 将四边形的问题转化为三角形,利用三角形的全等来解决,学会将未知转化为已知的解题思路——化归思想。辅助线:连接对角线符号语言∵ ,
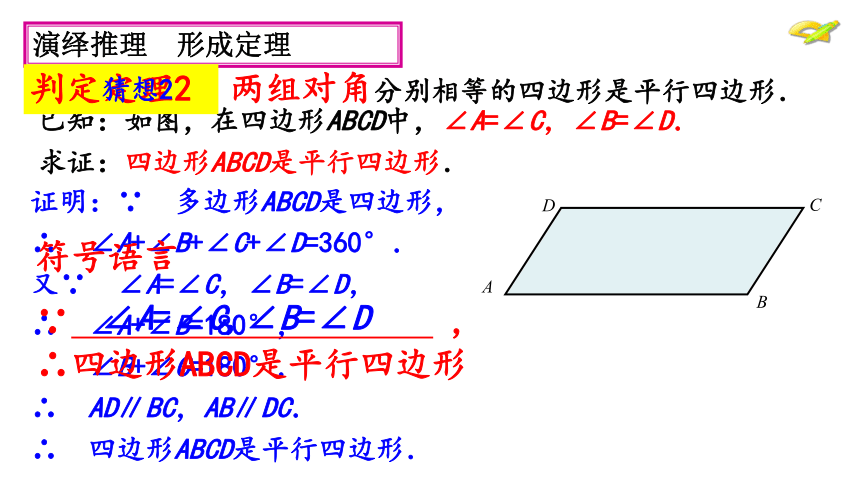
∴四边形ABCD是平行四边形归纳总结∵ AB=CD ,AD=BC证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形. 已知:如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形. 演绎推理 形成定理 两组对角分别相等的四边形是平行四边形. 判定定理2 猜想2 符号语言
∵ , ∴四边形ABCD是平行四边形 ∠A=∠C,∠B=∠D 已知:如图,在四边形ABCD中,AC,BD相交于点 O,
且OA=OC,OB=OD. 求证:四边形ABCD是平行四边形. 演绎推理 形成定理 对角线互相平分的四边形是平行四边形. 判定定理3 猜想3 证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴ △AOD≌△COB.
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形符号语言∵ ,
∴四边形ABCD是平行四边形OA=OC ,OB=OD两组对边分别平行的四边形是平行四边形
(定义)判定1 两组对边分别相等的四边形是平行四边形判定2 两组对角分别相等的四边形是平行四边形判定3 对角线互相平分的四边形是平行四边形∵AB∥CD, AD∥BC
∴四边形ABCD是
平行四边形∵OA=OC, OB=OD
∴四边形ABCD是
平行四边形∵∠A=∠C, ∠B=∠D
∴四边形ABCD是
平行四边形∵AB=CD, AD= BC
∴四边形ABCD是
平行四边形边对角线角归纳总结平行四边形的判定定理性质判定互为逆定理例1 填空:如图在四边形ABCD中(1)若AB//CD,补充条件 ,使四边形ABCD为平行四边形.
(2)若AB=CD,补充条件 ,使四边形ABCD为平行四边形.
(3)若对角线AC、BD交于点O,OA=OC=3,OB=5,
补充条件 ,使四边形ABCD为平行四边形.方法归纳:紧扣平行四边形的判定方法补上缺失条件.AD//BCAD=BCOD=5典例精析初识判定1、判断下列四边形是否是平行四边形?并口述理由.⑴O⑵尝试练习2、(1)(2015 昆明)在四边形ABCD中,对角线AC、BD相
交于点O,下列条件不能判定四边形ABCD为平行
四边形的是( )
A、AB∥CD,AD∥BC B、OA=OC,OB=OD
C、AD=BC,AB∥CD D、AB=CD,AD=BC(2)下面给出了四边形ABCD中,∠A,∠B,∠C,∠D
的度数之比,其中能判定四边形ABCD是平行四
边形的是( )
A、1 : 2 : 3 : 4 B、2 : 2 : 3 : 3
C、2 : 3 : 2 : 3 D、2 : 3 : 3 : 2CC例2.已知:平行四边形ABCD的对角线AC,BD相交于点O, E、F对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形证法1:
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
性质判定3
对角线∵ AE=CF
∴ AO-AE=CO-CF
∴ EO=FO
又 ∵ BO=DO
∴ 四边形BFDE是平行四边形
例2.已知:平行四边形ABCD的对角线AC,BD相交于点O, E、F对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形一题多解,最优法判定1 边全等三
角形 思考:我们知道,两组对边分别平行或相等的四边形是平行四边形,如果只考虑四边形的一组对边,他们满足什么条件时这个四边形能成为平行四边形呢? 猜想:一组对边平行且相等的四边形是平形四边形。探究新知2一组对边平行且相等的四边形是平行四边形. 已知:如图,在四边形ABCD中,AD//BC且AD=BC,
求证: 四边形ABCD是平行四边形 . 证明:连结AC ∵ AD∥BC∴∠1=∠2AC=CA(公共边)∴△ABC ≌ △CDA (SAS) CB=AD(已知)∠2=∠1(已知)在△ABC 和△CDA中 ∴四边形ABCD是平行四边形DBAC ∴AB=DC∵ AD=BC猜想4 判定定理4 演绎推理 形成定理 连接对角线∴ ∠ACD=∠CAB
∴ AB∥CD
∵ AD∥BC
一组对边平行且相等的四边形是平行四边形.在四边形ABCD中,
∵ , ∴四边形ABCD是平行四边形.符号语言:强调:同一组对边平行且相等.归纳总结判定定理4AB//CD,AB =CD,AD//BC,AD =BC,判定
方法1
(边)定义法(边)判定
方法2 (角)判定
方法3
(对角线)两组对边分别平行的四边形是平行四边形∵AB//CD, AD//BC,
∴四边形ABCD是
平行四边形 ∵AB=CD,AD=BC,
∴四边形ABCD是
平行四边形 ∵ ∠ A= ∠ C,
∠ B= ∠ D,
∴四边形ABCD是
平行四边形 ∵AO=CO,BO=DO,
∴四边形ABCD是
平行四边形两组对角分别相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形对角线互相平分的四边形是平行四边形判定
方法4 (边)一组对边平行且相等的四边形是平行四边形∵AB//CD, AB=CD,
∴四边形ABCD是
平行四边形 平行四边形的判定方法1、在下列条件中,不能判定四边形是平行四边形的有( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠CD(两组对边分别平行)(两组对边分别相等)(一组对边平行且相等)(两组对角分别相等)尝试练习例3、已知:如图,E,F分别是 平行四边形ABCD 的边AD,BC的中点。
求证:BE=DF.D证明:∵四边形ABCD是平行四边形,∴AD∥BC AD=BC∵E,F分别是AD,BC的中点,∴ED=BF。∴四边形EBFD是平行四边形(一组对边平行且相等的四边形是平行四边形)
∴BE=DF典例精析三角形全等平行四边形的判定和性质一题多解,合理选择判定。性质判定4性质证明:连接BD交AC于点O.
∵四边形ABCD是平行四边形
∴BO=DO
又∵ AE=CF, ∴OE=OF
∴ 四边形BFDE是平行四边形1、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形DABCEF变式:将AE=CF改为 “ BE垂直AC,DF垂直AC呢?”连接对角线综合应用多题归一,合理选择从边来判定1、两组对边分别平行的四边形是
平行四边形. 2、两组对边分别相等的四边形是
平行四边形.从角来判定4、两组对角分别相等的四边形是
平行四边形.从对角线来判定5、两条对角线互相平分的四边形
是平行四边形.平行四边形的判定方法3、一组对边平行且相等的四边形
是平行四边形.课堂小结知识技能性质判定互为逆定理研究图形的一般思路. 解题策略的角度:
证明平行四边形有多种方法,应根据条件灵活选择判定.常用辅助线:连接对角线 数学核心素养过程与方法的角度:
1.下列条件能判断四边形ABDC是平行四边形的是( )
A.AB∥CD,AC=B D
B.AB= CD ,AC=B D
C.AB=CD, AD=BC
D.AB=CD,OA=OC
2.已知:如图,平行四边形ABCD中,点E、F分别在CD、AB上的动点,且CE=AF,连接DF,BE,EF交BD于点O.求证: OE=OF.当堂检测B课后作业必做题:1、写出判定定理2,3的证明过程。
2、课本47页 练习 第1、2、3、4题.选做题: 一天八年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)请用尽可能多的方法解决本题。生活实际的挑战祝同学们:
身体健康,学习进步!
引入讲授
新课归纳
总结情景
引入导入
新课课后
作业1.八下数学课本(翻到18.1.2平行四边形的判定)
2.平行四边形的判定导学案(练习本)
3.双色笔(红和黑)
4.刻度尺或三角板。学习工具准备:课前准备平行四边形的定义:
符号语言
∵四边形ABCD是平行四边形
∴ AB//CD,AD//BC温故知新
对边分别 的四边形叫做平行四边形。
性质两组平行平行四边形的对边平行且相等。 平行四边形的对角线互相平分。平行四边
形的性质平行四边形的对角相等。
∵四边形ABCD是平行边形
∴ ∠A=∠ C, ∠ D=∠ B
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD性质定义判定平行四边形学习重点、难点重点:平行四边形判定方法的探究.
难点:平行四边形判定方法的理解和灵活应用.
学习目标1.经历平行四边形判定定理的猜想与证明过程,
体会类比、转化的思想及探究图形判定的一般思路.
2.掌握平行四边形的判定定理,能根据不同条件灵活选取适当的判定定理进行推理论证.
平行四边形的定义:
两组对边分别平行的四边形叫做平行四边形
符号语言
∵AB//CD,AD//BC
∴ .
探究新知1定义是平行四边形的原始的判定方法定义法四边形ABCD是平行四边形
1、平行四边形的两组对边分别相等;(边)
2、平行四边形的两组对角分别相等; (角)
3、平行四边形的对角线互相平分.(对角线)问题:
请写出以上命题的逆命题.逆命题: 1、两组对边分别相等的四边形是平行四边形.2、两组对角分别相等的四边形是平行四边形.3、对角线互相平分的四边形是平行四边形.平行四边形的性质:1、两组对边分别相等的四边形是平行四边形。2、两组对角分别相等的四边形是平行四边形。3、对角线互相平分的四边形是平行四边形.
平行四边形
的判定定理猜想:这些命题一定成立吗?如何证明?BDAC 四边形ABCD是平行四边形AB∥ CD,AD ∥ BC△ABC≌△CDA∠BAC=∠DCA,∠ACB=∠CAD(S.S.S)平行四边形(证明角相等)思路:定义法转
化连
接
对
角
线已知:在四边形ABCD中, ,
求证: 。 AB=CD,AD=BC四边形ABCD是平行四边形两组对边分别相等的四边形是平行四边形证明猜想1 演绎推理 形成定理 证明:连接AC在△ABC和△CDA中∴△ABC≌△CDA(SSS)
∴∠BAC=∠DCA,∠ACB=∠CAD(全等三角形的对应角相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是平行四边形)
已知:四边形ABCD中,AB=CD,AD=BC
求证:四边形ABCD是平行四边形两组对边分别相等的四边形是平行四边形。判定定理1猜想1两组对边分别相等的四边形是平行四边形。判定定理1 将四边形的问题转化为三角形,利用三角形的全等来解决,学会将未知转化为已知的解题思路——化归思想。辅助线:连接对角线符号语言∵ ,
∴四边形ABCD是平行四边形归纳总结∵ AB=CD ,AD=BC证明:∵ 多边形ABCD是四边形,
∴ ∠A+∠B+∠C+∠D=360°.
又∵ ∠A=∠C,∠B=∠D,
∴ ∠A+∠B=180°,
∠B+∠C=180°.
∴ AD∥BC,AB∥DC.
∴ 四边形ABCD是平行四边形. 已知:如图,在四边形ABCD中,∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形. 演绎推理 形成定理 两组对角分别相等的四边形是平行四边形. 判定定理2 猜想2 符号语言
∵ , ∴四边形ABCD是平行四边形 ∠A=∠C,∠B=∠D 已知:如图,在四边形ABCD中,AC,BD相交于点 O,
且OA=OC,OB=OD. 求证:四边形ABCD是平行四边形. 演绎推理 形成定理 对角线互相平分的四边形是平行四边形. 判定定理3 猜想3 证明:∵ OA=OC,OB=OD,∠AOD=∠COB,
∴ △AOD≌△COB.
∴ ∠OAD=∠OCB.
∴ AD∥BC.
同理 AB∥DC.
∴ 四边形ABCD是平行四边形符号语言∵ ,
∴四边形ABCD是平行四边形OA=OC ,OB=OD两组对边分别平行的四边形是平行四边形
(定义)判定1 两组对边分别相等的四边形是平行四边形判定2 两组对角分别相等的四边形是平行四边形判定3 对角线互相平分的四边形是平行四边形∵AB∥CD, AD∥BC
∴四边形ABCD是
平行四边形∵OA=OC, OB=OD
∴四边形ABCD是
平行四边形∵∠A=∠C, ∠B=∠D
∴四边形ABCD是
平行四边形∵AB=CD, AD= BC
∴四边形ABCD是
平行四边形边对角线角归纳总结平行四边形的判定定理性质判定互为逆定理例1 填空:如图在四边形ABCD中(1)若AB//CD,补充条件 ,使四边形ABCD为平行四边形.
(2)若AB=CD,补充条件 ,使四边形ABCD为平行四边形.
(3)若对角线AC、BD交于点O,OA=OC=3,OB=5,
补充条件 ,使四边形ABCD为平行四边形.方法归纳:紧扣平行四边形的判定方法补上缺失条件.AD//BCAD=BCOD=5典例精析初识判定1、判断下列四边形是否是平行四边形?并口述理由.⑴O⑵尝试练习2、(1)(2015 昆明)在四边形ABCD中,对角线AC、BD相
交于点O,下列条件不能判定四边形ABCD为平行
四边形的是( )
A、AB∥CD,AD∥BC B、OA=OC,OB=OD
C、AD=BC,AB∥CD D、AB=CD,AD=BC(2)下面给出了四边形ABCD中,∠A,∠B,∠C,∠D
的度数之比,其中能判定四边形ABCD是平行四
边形的是( )
A、1 : 2 : 3 : 4 B、2 : 2 : 3 : 3
C、2 : 3 : 2 : 3 D、2 : 3 : 3 : 2CC例2.已知:平行四边形ABCD的对角线AC,BD相交于点O, E、F对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形证法1:
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
性质判定3
对角线∵ AE=CF
∴ AO-AE=CO-CF
∴ EO=FO
又 ∵ BO=DO
∴ 四边形BFDE是平行四边形
例2.已知:平行四边形ABCD的对角线AC,BD相交于点O, E、F对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形一题多解,最优法判定1 边全等三
角形 思考:我们知道,两组对边分别平行或相等的四边形是平行四边形,如果只考虑四边形的一组对边,他们满足什么条件时这个四边形能成为平行四边形呢? 猜想:一组对边平行且相等的四边形是平形四边形。探究新知2一组对边平行且相等的四边形是平行四边形. 已知:如图,在四边形ABCD中,AD//BC且AD=BC,
求证: 四边形ABCD是平行四边形 . 证明:连结AC ∵ AD∥BC∴∠1=∠2AC=CA(公共边)∴△ABC ≌ △CDA (SAS) CB=AD(已知)∠2=∠1(已知)在△ABC 和△CDA中 ∴四边形ABCD是平行四边形DBAC ∴AB=DC∵ AD=BC猜想4 判定定理4 演绎推理 形成定理 连接对角线∴ ∠ACD=∠CAB
∴ AB∥CD
∵ AD∥BC
一组对边平行且相等的四边形是平行四边形.在四边形ABCD中,
∵ , ∴四边形ABCD是平行四边形.符号语言:强调:同一组对边平行且相等.归纳总结判定定理4AB//CD,AB =CD,AD//BC,AD =BC,判定
方法1
(边)定义法(边)判定
方法2 (角)判定
方法3
(对角线)两组对边分别平行的四边形是平行四边形∵AB//CD, AD//BC,
∴四边形ABCD是
平行四边形 ∵AB=CD,AD=BC,
∴四边形ABCD是
平行四边形 ∵ ∠ A= ∠ C,
∠ B= ∠ D,
∴四边形ABCD是
平行四边形 ∵AO=CO,BO=DO,
∴四边形ABCD是
平行四边形两组对角分别相等的四边形是平行四边形两组对边分别相等的四边形是平行四边形对角线互相平分的四边形是平行四边形判定
方法4 (边)一组对边平行且相等的四边形是平行四边形∵AB//CD, AB=CD,
∴四边形ABCD是
平行四边形 平行四边形的判定方法1、在下列条件中,不能判定四边形是平行四边形的有( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠CD(两组对边分别平行)(两组对边分别相等)(一组对边平行且相等)(两组对角分别相等)尝试练习例3、已知:如图,E,F分别是 平行四边形ABCD 的边AD,BC的中点。
求证:BE=DF.D证明:∵四边形ABCD是平行四边形,∴AD∥BC AD=BC∵E,F分别是AD,BC的中点,∴ED=BF。∴四边形EBFD是平行四边形(一组对边平行且相等的四边形是平行四边形)
∴BE=DF典例精析三角形全等平行四边形的判定和性质一题多解,合理选择判定。性质判定4性质证明:连接BD交AC于点O.
∵四边形ABCD是平行四边形
∴BO=DO
又∵ AE=CF, ∴OE=OF
∴ 四边形BFDE是平行四边形1、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF.
求证:四边形BFDE是平行四边形DABCEF变式:将AE=CF改为 “ BE垂直AC,DF垂直AC呢?”连接对角线综合应用多题归一,合理选择从边来判定1、两组对边分别平行的四边形是
平行四边形. 2、两组对边分别相等的四边形是
平行四边形.从角来判定4、两组对角分别相等的四边形是
平行四边形.从对角线来判定5、两条对角线互相平分的四边形
是平行四边形.平行四边形的判定方法3、一组对边平行且相等的四边形
是平行四边形.课堂小结知识技能性质判定互为逆定理研究图形的一般思路. 解题策略的角度:
证明平行四边形有多种方法,应根据条件灵活选择判定.常用辅助线:连接对角线 数学核心素养过程与方法的角度:
1.下列条件能判断四边形ABDC是平行四边形的是( )
A.AB∥CD,AC=B D
B.AB= CD ,AC=B D
C.AB=CD, AD=BC
D.AB=CD,OA=OC
2.已知:如图,平行四边形ABCD中,点E、F分别在CD、AB上的动点,且CE=AF,连接DF,BE,EF交BD于点O.求证: OE=OF.当堂检测B课后作业必做题:1、写出判定定理2,3的证明过程。
2、课本47页 练习 第1、2、3、4题.选做题: 一天八年级的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来,然后带上图纸去就行了,可原来的平行四边形怎么画出来呢?(A,B,C为三顶点,即找出第四个顶点D)请用尽可能多的方法解决本题。生活实际的挑战祝同学们:
身体健康,学习进步!
