人教版七年级数学下册 5.1.1 相交线 课件 (共27张PPT)
文档属性
| 名称 | 人教版七年级数学下册 5.1.1 相交线 课件 (共27张PPT) | 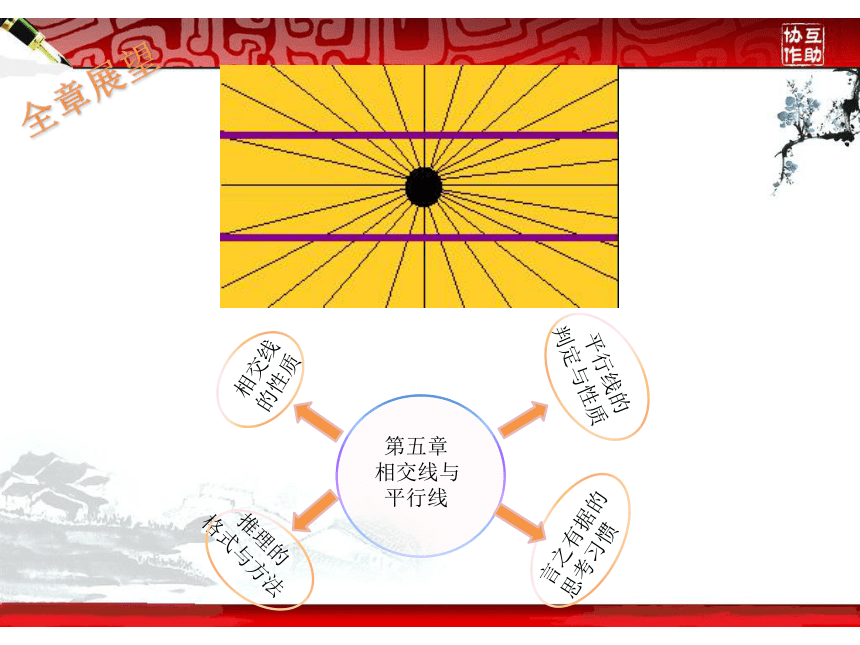 | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-21 23:50:31 | ||
图片预览






文档简介
(共27张PPT)
全章展望
第五章
第五章
相交线与
平行线
相交线
的性质
平行线的
判定与性质
推理的
格式与方法
言之有据的思考习惯
这里有一把剪刀,握紧剪刀的把手,就能剪开物体,
你能说出其中的道理吗?
探究新知
如果把剪子的构造抽象成一个几何图形,会是什么
样的图形?请你在笔记本上画出.
探究新知
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
§5.1.1相交线
学习目标:
(1)理解邻补角和对顶角的概念.
(2)掌握“对顶角相等”的性质.
学习重点:
对顶角相等的性质.
§5.1.1相交线
指南罗盘
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
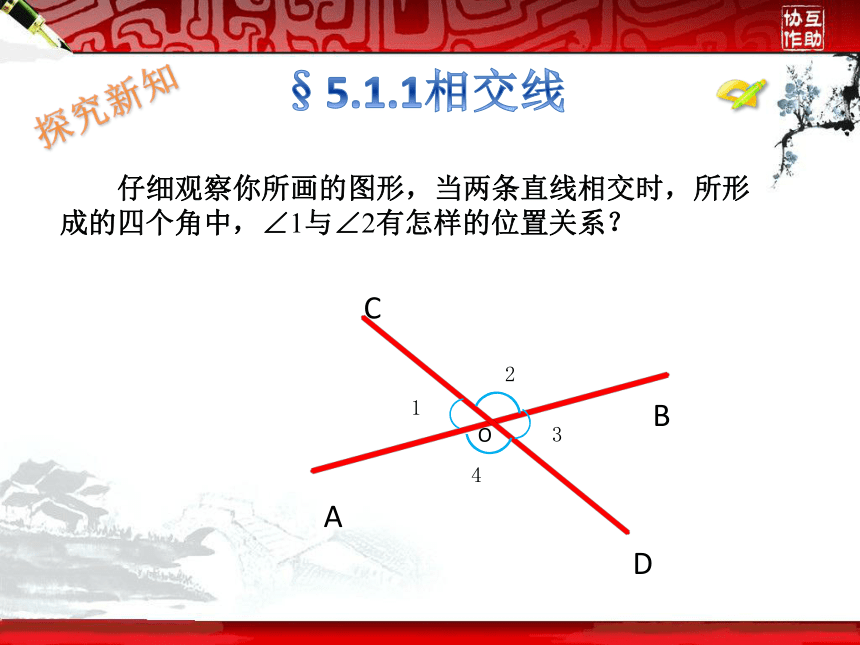
§5.1.1相交线
仔细观察你所画的图形,当两条直线相交时,所形成的四个角中,∠1与∠2有怎样的位置关系?
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
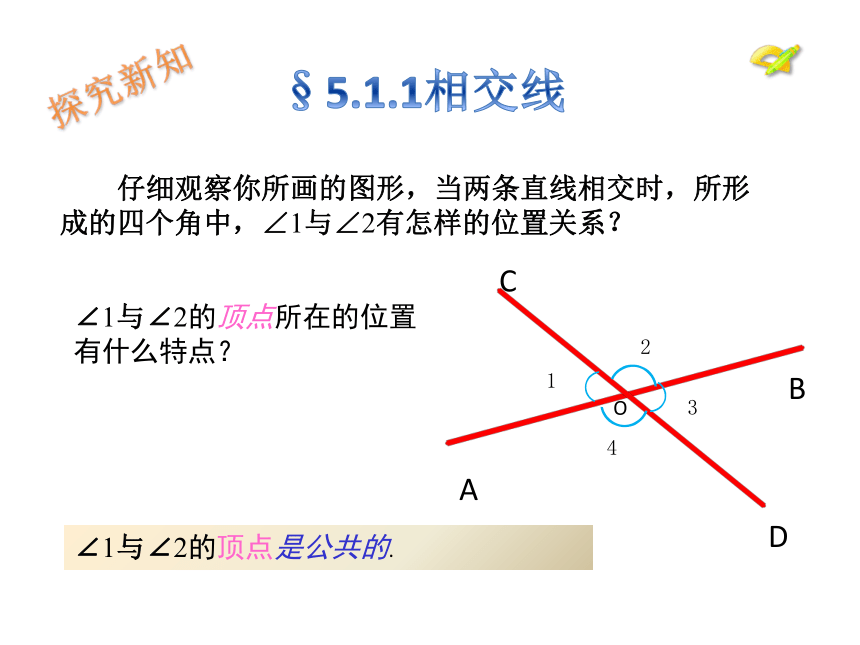
§5.1.1相交线
仔细观察你所画的图形,当两条直线相交时,所形成的四个角中,∠1与∠2有怎样的位置关系?
∠1与∠2的顶点所在的位置有什么特点?
∠1与∠2的顶点是公共的.
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
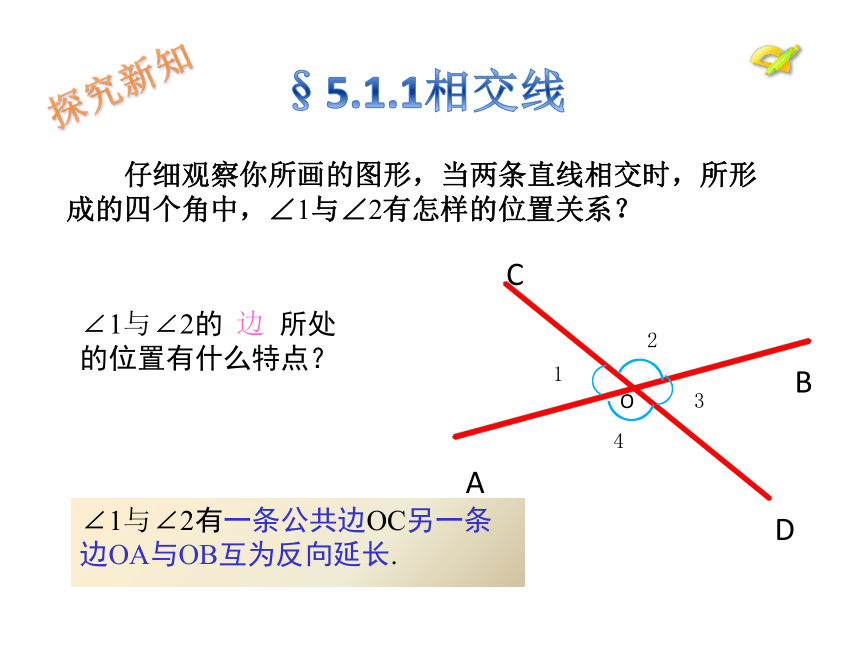
§5.1.1相交线
仔细观察你所画的图形,当两条直线相交时,所形成的四个角中,∠1与∠2有怎样的位置关系?
∠1与∠2的 边 所处的位置有什么特点?
∠1与∠2有一条公共边OC另一条边OA与OB互为反向延长.
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
§5.1.1相交线
邻补角的定义:有一条公共边,它们的另一边互为反向延长线的两个角,互为邻补角.
图中还有哪些邻补角?
还有:∠1与∠4;
∠2与∠3;
∠3与∠4.
互补的两个角是邻补角吗?
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
§5.1.1相交线
邻补角的定义:有一条公共边,它们的另一边互为反向延长线的两个角,互为邻补角.
由邻补角定义你能不能说说∠1和∠2有什么数量关系?
互 补
邻补角性质:邻补角互补
例 1(1)下列各图中,∠1和∠2是邻补角吗?为什么?
(1) (2) (3)
1
2
1
1
2
2
学以致用
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
§5.1.1相交线
仔细观察你所画的图形,当两条直线相交时,所形成的四个角中,∠1与∠3有怎样的位置关系?
有一个公共顶点,两条边都互为反向延长线.
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
§5.1.1相交线
对顶角的定义:其中一个角的两边分别是另一个角的两边的反向延长线的两个角,互为对顶角.
图中还有对顶角吗?
∠2与∠4
1
2
(2)
(3)
(4)
2
1
(1)
1
2
(5)
1
2
1
2
例 1(2)下列各图中,∠1和∠2是对顶角吗?为什么?
学以致用
例 1(3)请分别画出图中∠1的对顶角和∠2的邻补角.
2
1
α
β
θ
学以致用
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
§5.1.1相交线
仔细观察图形,∠1与∠3有怎样的数量关系?
你是怎么得到的?
相 等
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
§5.1.1相交线
你能说出∠1=∠3的道理吗?请你用数学的语言写出这个过程.
∵直线AB与CD相交于点O.(已知)
∴∠1+∠2 =180°,
∠3+∠2 =180°(邻补角定义).
∴∠1=∠3 (同角的补角相等).
于是:
对顶角性质:对顶角相等。
例2 如图,直线a,b相交于点O,∠1 =40? ,
求∠2 ,∠3 ,∠4 的度数.
1
2
3
4
a
b
O
学以致用
解:(1)∵直线a与b相交于点O(已知).
∴∠1+∠2=180°,
∠1+∠4=180°(邻补角定义),
∠3=∠1 (对顶角相等).
∵∠1=40°(已知).
∴∠2=140°,∠4=140°
∠3=40°.
例2 如图,直线a,b相交于点O,∠1 =40? ,
求∠2 ,∠3 ,∠4 的度数.
1
2
3
4
a
b
O
变式2 :若∠2是∠1的 3.5倍,
求各个角的度数.
变式1 :若∠1+∠3= 80? ,
求各个角的度数.
变式3 :若 ∠1: ∠2 = 2: 7 ,
求各个角的度数.
大脑转转
§5.1.1相交线
课堂小结
4.邻补角与补角的关系:
2.邻补角: (1)定义(位置关系);(2)性质(数量关系).
3.对顶角: (1)定义(位置关系)(2)性质(数量关系).
1.全章展望:
5.对顶角性质的证明:
角的
名称 特 征 性 质 相 同 点 不 同 点
对
顶
角
邻
补
角
对顶
角相
等
邻补
角互
补
②有公共顶点;
③没有公共边
①两条直线相交形成的角;
①两条直线相交而成;
②有公共顶点;
③有一条公共边
①都是两条直线相交而成的角;
③都是成对出现的
②都有一个公共顶点;
②两直线相交时,对顶角只有两对,邻补角有四对
①有无公共边;
课堂小结
达标检测
利用的原理是:对顶角相等
∠BOD或∠AOC
∠AOD
50°
§5.1.1相交线
达标检测
20°
70°
160°
§5.1.1相交线
如图,直线AB与CD相交于点O,OA平分∠COE,
(1)若∠COE=70°,求∠BOD的度数.
(2)若∠COE∶∠DOE=2∶3,求∠BOD的度数.
达标检测
§5.1.1相交线
解:(1)∵直线AB与CD相交于点O(已知).
∴∠BOD=∠AOC(对顶角相等).
∵OA平分∠EOC(已知).
∴∠AOC=1/2∠EOC(角的平分线定义).
∵∠EOC=70°(已知).
∴∠AOC=35°.
∴∠BOD=35°.
达标检测
§5.1.1相交线
(2)∵直线AB与CD相交于点O(已知).
∴∠COE+∠DOE=180°(邻补角定义).
∵∠COE∶∠DOE=2∶3(已知).
∴∠COE=(2/5)×180°=72°
由(1)∠AOC=(1/2)∠COE,
∠BOD=∠AOC.
∴∠BOD=36°.
达标检测
§5.1.1相交线
教科书 习题5.1 第1、2题.
§5.1.1相交线
布置作业
全章展望
第五章
第五章
相交线与
平行线
相交线
的性质
平行线的
判定与性质
推理的
格式与方法
言之有据的思考习惯
这里有一把剪刀,握紧剪刀的把手,就能剪开物体,
你能说出其中的道理吗?
探究新知
如果把剪子的构造抽象成一个几何图形,会是什么
样的图形?请你在笔记本上画出.
探究新知
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
§5.1.1相交线
学习目标:
(1)理解邻补角和对顶角的概念.
(2)掌握“对顶角相等”的性质.
学习重点:
对顶角相等的性质.
§5.1.1相交线
指南罗盘
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
§5.1.1相交线
仔细观察你所画的图形,当两条直线相交时,所形成的四个角中,∠1与∠2有怎样的位置关系?
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
§5.1.1相交线
仔细观察你所画的图形,当两条直线相交时,所形成的四个角中,∠1与∠2有怎样的位置关系?
∠1与∠2的顶点所在的位置有什么特点?
∠1与∠2的顶点是公共的.
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
§5.1.1相交线
仔细观察你所画的图形,当两条直线相交时,所形成的四个角中,∠1与∠2有怎样的位置关系?
∠1与∠2的 边 所处的位置有什么特点?
∠1与∠2有一条公共边OC另一条边OA与OB互为反向延长.
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
§5.1.1相交线
邻补角的定义:有一条公共边,它们的另一边互为反向延长线的两个角,互为邻补角.
图中还有哪些邻补角?
还有:∠1与∠4;
∠2与∠3;
∠3与∠4.
互补的两个角是邻补角吗?
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
§5.1.1相交线
邻补角的定义:有一条公共边,它们的另一边互为反向延长线的两个角,互为邻补角.
由邻补角定义你能不能说说∠1和∠2有什么数量关系?
互 补
邻补角性质:邻补角互补
例 1(1)下列各图中,∠1和∠2是邻补角吗?为什么?
(1) (2) (3)
1
2
1
1
2
2
学以致用
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
§5.1.1相交线
仔细观察你所画的图形,当两条直线相交时,所形成的四个角中,∠1与∠3有怎样的位置关系?
有一个公共顶点,两条边都互为反向延长线.
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
§5.1.1相交线
对顶角的定义:其中一个角的两边分别是另一个角的两边的反向延长线的两个角,互为对顶角.
图中还有对顶角吗?
∠2与∠4
1
2
(2)
(3)
(4)
2
1
(1)
1
2
(5)
1
2
1
2
例 1(2)下列各图中,∠1和∠2是对顶角吗?为什么?
学以致用
例 1(3)请分别画出图中∠1的对顶角和∠2的邻补角.
2
1
α
β
θ
学以致用
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
§5.1.1相交线
仔细观察图形,∠1与∠3有怎样的数量关系?
你是怎么得到的?
相 等
探究新知
O
⌒
⌒
⌒
⌒
1
2
3
4
A
D
B
C
§5.1.1相交线
你能说出∠1=∠3的道理吗?请你用数学的语言写出这个过程.
∵直线AB与CD相交于点O.(已知)
∴∠1+∠2 =180°,
∠3+∠2 =180°(邻补角定义).
∴∠1=∠3 (同角的补角相等).
于是:
对顶角性质:对顶角相等。
例2 如图,直线a,b相交于点O,∠1 =40? ,
求∠2 ,∠3 ,∠4 的度数.
1
2
3
4
a
b
O
学以致用
解:(1)∵直线a与b相交于点O(已知).
∴∠1+∠2=180°,
∠1+∠4=180°(邻补角定义),
∠3=∠1 (对顶角相等).
∵∠1=40°(已知).
∴∠2=140°,∠4=140°
∠3=40°.
例2 如图,直线a,b相交于点O,∠1 =40? ,
求∠2 ,∠3 ,∠4 的度数.
1
2
3
4
a
b
O
变式2 :若∠2是∠1的 3.5倍,
求各个角的度数.
变式1 :若∠1+∠3= 80? ,
求各个角的度数.
变式3 :若 ∠1: ∠2 = 2: 7 ,
求各个角的度数.
大脑转转
§5.1.1相交线
课堂小结
4.邻补角与补角的关系:
2.邻补角: (1)定义(位置关系);(2)性质(数量关系).
3.对顶角: (1)定义(位置关系)(2)性质(数量关系).
1.全章展望:
5.对顶角性质的证明:
角的
名称 特 征 性 质 相 同 点 不 同 点
对
顶
角
邻
补
角
对顶
角相
等
邻补
角互
补
②有公共顶点;
③没有公共边
①两条直线相交形成的角;
①两条直线相交而成;
②有公共顶点;
③有一条公共边
①都是两条直线相交而成的角;
③都是成对出现的
②都有一个公共顶点;
②两直线相交时,对顶角只有两对,邻补角有四对
①有无公共边;
课堂小结
达标检测
利用的原理是:对顶角相等
∠BOD或∠AOC
∠AOD
50°
§5.1.1相交线
达标检测
20°
70°
160°
§5.1.1相交线
如图,直线AB与CD相交于点O,OA平分∠COE,
(1)若∠COE=70°,求∠BOD的度数.
(2)若∠COE∶∠DOE=2∶3,求∠BOD的度数.
达标检测
§5.1.1相交线
解:(1)∵直线AB与CD相交于点O(已知).
∴∠BOD=∠AOC(对顶角相等).
∵OA平分∠EOC(已知).
∴∠AOC=1/2∠EOC(角的平分线定义).
∵∠EOC=70°(已知).
∴∠AOC=35°.
∴∠BOD=35°.
达标检测
§5.1.1相交线
(2)∵直线AB与CD相交于点O(已知).
∴∠COE+∠DOE=180°(邻补角定义).
∵∠COE∶∠DOE=2∶3(已知).
∴∠COE=(2/5)×180°=72°
由(1)∠AOC=(1/2)∠COE,
∠BOD=∠AOC.
∴∠BOD=36°.
达标检测
§5.1.1相交线
教科书 习题5.1 第1、2题.
§5.1.1相交线
布置作业
