【人教版七年级数学下册同步精选】6.1 平方根同步精选练习题(含解析)
文档属性
| 名称 | 【人教版七年级数学下册同步精选】6.1 平方根同步精选练习题(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 465.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-22 00:00:00 | ||
图片预览




文档简介
6.1平方根同步精选练习题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各等式中,正确的是( )
A.=±4 B.±=4 C.=﹣5 D.
2.正方形的面积为6,则正方形的边长为( )
A. B. C.2 D.4
3.正数9的平方根是( )
A.3 B.±3 C. D.
4.下列说法正确的是( )
A.(﹣3)2的平方根是3 B.=±4
C.1的平方根是1 D.4的算术平方根是2
5.的算术平方根是( )
A.9 B.±9 C.±3 D.3
6.的平方根是( )
A.2 B. C.±2 D.±
7.如果=4,那么x等于( )
A.2 B. C.4 D.
二、填空题
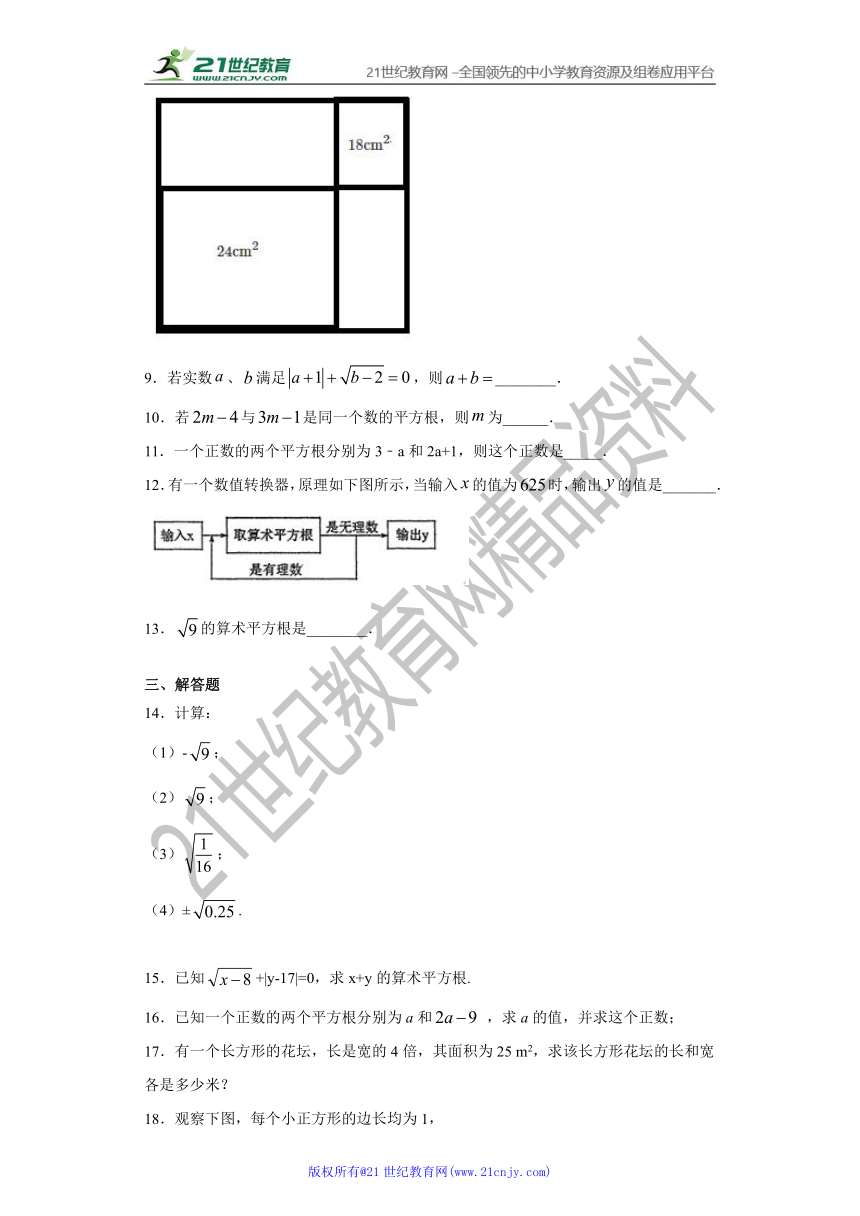
8.如图,从一个大正方形中截去面积为和的两个小正方形,则留下部分的面积为_____.
9.若实数、满足,则________.
10.若与是同一个数的平方根,则为______.
11.一个正数的两个平方根分别为3﹣a和2a+1,则这个正数是_____.
12.有一个数值转换器,原理如下图所示,当输入的值为时,输出的值是_______.
13.的算术平方根是________.
三、解答题
14.计算:
(1)-;
(2);
(3);
(4)±.
15.已知+|y-17|=0,求x+y的算术平方根.
16.已知一个正数的两个平方根分别为a和 ,求a的值,并求这个正数;
17.有一个长方形的花坛,长是宽的4倍,其面积为25 m2,求该长方形花坛的长和宽各是多少米?
18.观察下图,每个小正方形的边长均为1,
(1)图中阴影部分的面积是多少?边长是多少?
(2)估计边长的值在哪两个整数之间.
19.已知a2=4,|b|=3.
(1)已知ab>0,求a+b的值;
(2)若|a-b|=b-a,求ab的值.
参考答案
1.D
【解析】
【分析】
根据算术平方根的运算方法及平方根的运算方法,进行相应运算,找到计算正确的选项即可.
【详解】
解:A、正数的算术平方根只有1个,故错误;
B、正数的平方根有2个,故错误;
C、所给二次根式的被开方数为负数,二次根式没有意义,故错误;
D、正确;
故选D.
【点睛】
此题考查算术平方根及平方根的相关运算;用到的知识点为:一个正数的算术平方根只有1个;一个正数的平方根有2个;二次根式有意义,被开方数为非负数.
2.B
【解析】
【分析】
根据正方形面积的求法即可求解.
【详解】
解:∵正方形的面积为6, ∴正方形的边长为. 故选:B.
【点睛】
本题考查了算术平方根,正方形的面积,解此题的关键是求出6的算术平方根.
3.B
【解析】
【分析】
根据平方根的定义可得
【详解】
因为 3的平方都等于9,所以答案为B
【点睛】
本题考查了平方根的定义,注意区分平方根和算术平方根。
4.D
【解析】
【分析】
根据平方根和算术平方根的定义解答即可.
【详解】
A、(﹣3)2的平方根是±3,故该项错误;B、,故该项错误;C、1的平方根是±1,故该项错误;D、4的算术平方根是2,故该项正确.故选D.
【点睛】
本题考查了平方根、算术平方根的定义,解决本题的关键是熟记平方根、算术平方根的定义.
5.D
【解析】
【分析】
根据算术平方根的定义求解.
【详解】
∵=9, 又∵(±3)2=9, ∴9的平方根是±3, ∴9的算术平方根是3. 即的算术平方根是3. 故选:D.
【点睛】
考核知识点:算术平方根.理解定义是关键.
6.D
【解析】
【分析】
先化简,然后再根据平方根的定义求解即可.
【详解】
∵=2,2的平方根是±,
∴的平方根是±.
故选D.
【点睛】
本题考查了平方根的定义以及算术平方根,先把正确化简是解题的关键,本题比较容易出错.
7.D
【解析】
【分析】
直接利用算术平方根的性质得出x的值.
【详解】
解:∵=4,
∴ ∴x=±4. 故选:D.
【点睛】
此题主要考查了算术平方根的性质与化简,正确掌握算术平方根的性质是解题关键.
8.
【解析】
【分析】
根据两个小正方形的面积,即可求出小正方形的边长,然后根据长方形的面积公式即可求出留下部分的面积.
【详解】
解:∵两个小正方形的面积分别为和
∴它们的边长分别为:,
∴留下部分的面积为
故答案为:.
【点睛】
此题考查的是算术平方根的应用,掌握长方形的面积公式、正方形的面积公式和算术平方根的定义是解决此题的关键.
9.1
【解析】
【分析】
先根据非负数的性质求出、的值,再求出的值即可.
【详解】
解:∵,∴,解得,,
∴.故答案为1.
【点睛】
本题考查的是非负数的性质,属于基础题型,熟知非负数的性质:几个非负数的和为0时,其中每一项必为0是解答此题的关键.
10.或
【解析】
【分析】
根据一个数的平方根相等或互为相反数,即可求出m的值.
【详解】
解:∵与是同一个数的平方根,
∴或,
解得:或;
故答案为:或.
【点睛】
本题考查了平方根的定义,解题的关键是熟练掌握平方根的定义.
11.49
【解析】
【分析】
根据正数的平方根互为相反数,两平方根相加等于0求出a值,再求出一个平方根,平方就可以得到这个正数.
【详解】
根据题意得3﹣a+2a+1=0,
解得:a=﹣4,
∴这个正数为(3﹣a)2=72=49,
故答案为:49.
【点睛】
本题考查了平方根的性质,熟知一个正数有两个平方根,它们互为相反数是解题的关键.
12.
【解析】
【分析】
根据数值转换器的原理,列出算式,即可得到答案.
【详解】
根据数值转换器的原理得:,,5的算术平方根是,
故答案是:.
【点睛】
本题主要考查根据程序图求值,根据原理,列出算式,是解题的关键.
13.
【解析】
【分析】
根据算术平方根的性质求出=3,再求出3的算术平方根即可.
【详解】
解:∵=3,3的算术平方根是,
∴的算术平方根是. 故答案为:.
【点睛】
本题考查算术平方根的概念和求法,正数的算术平方根是正数,0的算术平方根是0,负数没有平方根.
14.(1)-3; (2)3; (3);(4)±0.5
【解析】
【分析】
直接利用平方根定义解题即可
【详解】
(1)-=-3
(2)=3
(3)=
(4)±=±0.5
【点睛】
本题考查平方根的定义,熟练掌握定义是解题关键
15.5
【解析】
【分析】
根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.
【详解】
根据题意得:,
解得: ,
则x+y=25,算术平方根是:.
故答案是:5.
【点睛】
本题考查非负数的性质:算术平方根,非负数的性质:绝对值.
16.a=3;这个正数是9.
【解析】
【分析】
根据一个正数的两个平方根互为相反数求出a的值,利用平方根和平方的关系求出这个正数.
【详解】
解:由平方根的性质得,,
解得,
这个正数为;
故答案为:a=3;这个正数是9.
【点睛】
本题考查平方根.
17.长方形花坛的长和宽分别是10m,m
【解析】
试题分析:设长方形花坛的宽为x m(x>0),则长为4x m,根据长方形的面积公式列出关于x的方程,利用算术平方根的概念求出x的值.
解:设长方形花坛的宽为x m(x>0),则长为4x m.由题意,得4x2=25,x2=,x==,4x=10.
答:长方形花坛的长和宽分别是10m, m
18.(1)图中阴影部分的面积17,边长是;(2)边长的值在4与5之间
【解析】
【分析】
(1)由图形可以得到阴影正方形的面积等于原来大正方形的面积减去周围四个直角三角形的面积,由正方形的面积等于边长乘以边长,可以得到阴影正方形的边长; (2)根据,可以估算出边长的值在哪两个整数之间.
【详解】
(1)由图可知,图中阴影正方形的面积是:5×5?=17 则阴影正方形的边长为:
答:图中阴影部分的面积17,边长是
(2)∵
所以4<<5 ∴边长的值在4与5之间;
【点睛】
本题主要考查了无理数的估算及算术平方根的定义,解题主要利用了勾股定理和正方形的面积求解,有一定的综合性,解题关键是无理数的估算.
19.(1)5或-5;(2)6或-6.
【解析】
【分析】
(1)根据平方根和绝对值的意义先求出a和b,由ab>0进一步确定a和b,再代入a+b计算即可;
(2)由题意确定a和b,再代入ab计算即可.
【详解】
解:(1)∵a2=4,|b|=3.
∴
又∵ab>0,
∴a、b同号,即若a=2,则b=3,此时 a+b=2+3=5;
若a=-2,则b=-3,此时a+b=-2-3=-5;
故a+b的值为5或-5;
(2)若|a-b|=b-a,则
即若a=2,则b=3,此时ab=;
若a=-2,则b=3,此时ab=;
故ab的值为6或-6.
【点睛】
本题考查了平方根和绝对值,也考查了有理数的运算,要注意分类,不要漏解.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列各等式中,正确的是( )
A.=±4 B.±=4 C.=﹣5 D.
2.正方形的面积为6,则正方形的边长为( )
A. B. C.2 D.4
3.正数9的平方根是( )
A.3 B.±3 C. D.
4.下列说法正确的是( )
A.(﹣3)2的平方根是3 B.=±4
C.1的平方根是1 D.4的算术平方根是2
5.的算术平方根是( )
A.9 B.±9 C.±3 D.3
6.的平方根是( )
A.2 B. C.±2 D.±
7.如果=4,那么x等于( )
A.2 B. C.4 D.
二、填空题
8.如图,从一个大正方形中截去面积为和的两个小正方形,则留下部分的面积为_____.
9.若实数、满足,则________.
10.若与是同一个数的平方根,则为______.
11.一个正数的两个平方根分别为3﹣a和2a+1,则这个正数是_____.
12.有一个数值转换器,原理如下图所示,当输入的值为时,输出的值是_______.
13.的算术平方根是________.
三、解答题
14.计算:
(1)-;
(2);
(3);
(4)±.
15.已知+|y-17|=0,求x+y的算术平方根.
16.已知一个正数的两个平方根分别为a和 ,求a的值,并求这个正数;
17.有一个长方形的花坛,长是宽的4倍,其面积为25 m2,求该长方形花坛的长和宽各是多少米?
18.观察下图,每个小正方形的边长均为1,
(1)图中阴影部分的面积是多少?边长是多少?
(2)估计边长的值在哪两个整数之间.
19.已知a2=4,|b|=3.
(1)已知ab>0,求a+b的值;
(2)若|a-b|=b-a,求ab的值.
参考答案
1.D
【解析】
【分析】
根据算术平方根的运算方法及平方根的运算方法,进行相应运算,找到计算正确的选项即可.
【详解】
解:A、正数的算术平方根只有1个,故错误;
B、正数的平方根有2个,故错误;
C、所给二次根式的被开方数为负数,二次根式没有意义,故错误;
D、正确;
故选D.
【点睛】
此题考查算术平方根及平方根的相关运算;用到的知识点为:一个正数的算术平方根只有1个;一个正数的平方根有2个;二次根式有意义,被开方数为非负数.
2.B
【解析】
【分析】
根据正方形面积的求法即可求解.
【详解】
解:∵正方形的面积为6, ∴正方形的边长为. 故选:B.
【点睛】
本题考查了算术平方根,正方形的面积,解此题的关键是求出6的算术平方根.
3.B
【解析】
【分析】
根据平方根的定义可得
【详解】
因为 3的平方都等于9,所以答案为B
【点睛】
本题考查了平方根的定义,注意区分平方根和算术平方根。
4.D
【解析】
【分析】
根据平方根和算术平方根的定义解答即可.
【详解】
A、(﹣3)2的平方根是±3,故该项错误;B、,故该项错误;C、1的平方根是±1,故该项错误;D、4的算术平方根是2,故该项正确.故选D.
【点睛】
本题考查了平方根、算术平方根的定义,解决本题的关键是熟记平方根、算术平方根的定义.
5.D
【解析】
【分析】
根据算术平方根的定义求解.
【详解】
∵=9, 又∵(±3)2=9, ∴9的平方根是±3, ∴9的算术平方根是3. 即的算术平方根是3. 故选:D.
【点睛】
考核知识点:算术平方根.理解定义是关键.
6.D
【解析】
【分析】
先化简,然后再根据平方根的定义求解即可.
【详解】
∵=2,2的平方根是±,
∴的平方根是±.
故选D.
【点睛】
本题考查了平方根的定义以及算术平方根,先把正确化简是解题的关键,本题比较容易出错.
7.D
【解析】
【分析】
直接利用算术平方根的性质得出x的值.
【详解】
解:∵=4,
∴ ∴x=±4. 故选:D.
【点睛】
此题主要考查了算术平方根的性质与化简,正确掌握算术平方根的性质是解题关键.
8.
【解析】
【分析】
根据两个小正方形的面积,即可求出小正方形的边长,然后根据长方形的面积公式即可求出留下部分的面积.
【详解】
解:∵两个小正方形的面积分别为和
∴它们的边长分别为:,
∴留下部分的面积为
故答案为:.
【点睛】
此题考查的是算术平方根的应用,掌握长方形的面积公式、正方形的面积公式和算术平方根的定义是解决此题的关键.
9.1
【解析】
【分析】
先根据非负数的性质求出、的值,再求出的值即可.
【详解】
解:∵,∴,解得,,
∴.故答案为1.
【点睛】
本题考查的是非负数的性质,属于基础题型,熟知非负数的性质:几个非负数的和为0时,其中每一项必为0是解答此题的关键.
10.或
【解析】
【分析】
根据一个数的平方根相等或互为相反数,即可求出m的值.
【详解】
解:∵与是同一个数的平方根,
∴或,
解得:或;
故答案为:或.
【点睛】
本题考查了平方根的定义,解题的关键是熟练掌握平方根的定义.
11.49
【解析】
【分析】
根据正数的平方根互为相反数,两平方根相加等于0求出a值,再求出一个平方根,平方就可以得到这个正数.
【详解】
根据题意得3﹣a+2a+1=0,
解得:a=﹣4,
∴这个正数为(3﹣a)2=72=49,
故答案为:49.
【点睛】
本题考查了平方根的性质,熟知一个正数有两个平方根,它们互为相反数是解题的关键.
12.
【解析】
【分析】
根据数值转换器的原理,列出算式,即可得到答案.
【详解】
根据数值转换器的原理得:,,5的算术平方根是,
故答案是:.
【点睛】
本题主要考查根据程序图求值,根据原理,列出算式,是解题的关键.
13.
【解析】
【分析】
根据算术平方根的性质求出=3,再求出3的算术平方根即可.
【详解】
解:∵=3,3的算术平方根是,
∴的算术平方根是. 故答案为:.
【点睛】
本题考查算术平方根的概念和求法,正数的算术平方根是正数,0的算术平方根是0,负数没有平方根.
14.(1)-3; (2)3; (3);(4)±0.5
【解析】
【分析】
直接利用平方根定义解题即可
【详解】
(1)-=-3
(2)=3
(3)=
(4)±=±0.5
【点睛】
本题考查平方根的定义,熟练掌握定义是解题关键
15.5
【解析】
【分析】
根据非负数的性质列出方程求出x、y的值,代入所求代数式计算即可.
【详解】
根据题意得:,
解得: ,
则x+y=25,算术平方根是:.
故答案是:5.
【点睛】
本题考查非负数的性质:算术平方根,非负数的性质:绝对值.
16.a=3;这个正数是9.
【解析】
【分析】
根据一个正数的两个平方根互为相反数求出a的值,利用平方根和平方的关系求出这个正数.
【详解】
解:由平方根的性质得,,
解得,
这个正数为;
故答案为:a=3;这个正数是9.
【点睛】
本题考查平方根.
17.长方形花坛的长和宽分别是10m,m
【解析】
试题分析:设长方形花坛的宽为x m(x>0),则长为4x m,根据长方形的面积公式列出关于x的方程,利用算术平方根的概念求出x的值.
解:设长方形花坛的宽为x m(x>0),则长为4x m.由题意,得4x2=25,x2=,x==,4x=10.
答:长方形花坛的长和宽分别是10m, m
18.(1)图中阴影部分的面积17,边长是;(2)边长的值在4与5之间
【解析】
【分析】
(1)由图形可以得到阴影正方形的面积等于原来大正方形的面积减去周围四个直角三角形的面积,由正方形的面积等于边长乘以边长,可以得到阴影正方形的边长; (2)根据,可以估算出边长的值在哪两个整数之间.
【详解】
(1)由图可知,图中阴影正方形的面积是:5×5?=17 则阴影正方形的边长为:
答:图中阴影部分的面积17,边长是
(2)∵
所以4<<5 ∴边长的值在4与5之间;
【点睛】
本题主要考查了无理数的估算及算术平方根的定义,解题主要利用了勾股定理和正方形的面积求解,有一定的综合性,解题关键是无理数的估算.
19.(1)5或-5;(2)6或-6.
【解析】
【分析】
(1)根据平方根和绝对值的意义先求出a和b,由ab>0进一步确定a和b,再代入a+b计算即可;
(2)由题意确定a和b,再代入ab计算即可.
【详解】
解:(1)∵a2=4,|b|=3.
∴
又∵ab>0,
∴a、b同号,即若a=2,则b=3,此时 a+b=2+3=5;
若a=-2,则b=-3,此时a+b=-2-3=-5;
故a+b的值为5或-5;
(2)若|a-b|=b-a,则
即若a=2,则b=3,此时ab=;
若a=-2,则b=3,此时ab=;
故ab的值为6或-6.
【点睛】
本题考查了平方根和绝对值,也考查了有理数的运算,要注意分类,不要漏解.
