青岛版八年级数学下册第6章平行四边形单元测试含答案
文档属性
| 名称 | 青岛版八年级数学下册第6章平行四边形单元测试含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-22 11:12:56 | ||
图片预览


文档简介
平行四边形单元试卷
一、选择题(共12小题;共36分)
1. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是
A. ①② B. ①④ C. ③④ D. ②③
2. 如图,在 中,, 是 的中线, 与 相交于点 ,点 , 分别是 , 的中点,连接 .若 ,,则四边形 的周长是
A. B. C. D.
3. 如图,菱形 中,对角线 , 相交于点 , 为 边中点,菱形 的周长为 ,则 的长等于
A. B. C. D.
4. 如图,平行四边形 中,,, 于点 ,则 等于
A. B. C. D.
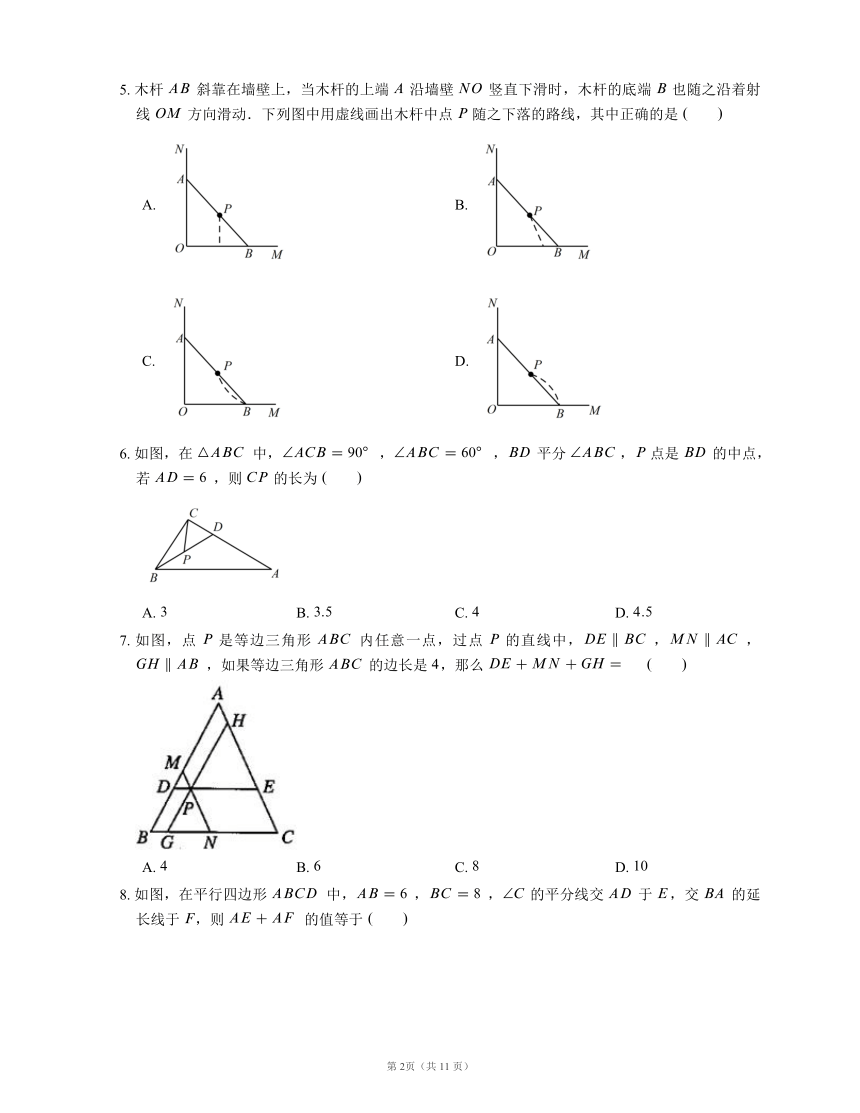
5. 木杆 斜靠在墙壁上,当木杆的上端 沿墙壁 竖直下滑时,木杆的底端 也随之沿着射线 方向滑动.下列图中用虚线画出木杆中点 随之下落的路线,其中正确的是
A. B.
C. D.
6. 如图,在 中,,, 平分 , 点是 的中点,若 ,则 的长为
A. B. C. D.
7. 如图,点 是等边三角形 内任意一点,过点 的直线中,,,,如果等边三角形 的边长是 ,那么
A. B. C. D.
8. 如图,在平行四边形 中,,, 的平分线交 于 ,交 的延长线于 ,则 的值等于
A. B. C. D.
9. 如图所示,四边形 中,,对角线 , 相交于点 , 于点 , 于点 ,连接 ,,若 ,则下列结论:① ;② ;③四边形 是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是
A. B. C. D.
10. 如图,在 中,, 的垂直平分线 交 于点 ,交 于点 ,且 .添加一个条件,仍不能证明四边形 为正方形的是
A. B. C. D.
11. 如图, 是正方形场地,点 在 的延长线上, 与 相交于点 .有甲、乙、丙三名同学同时从点 出发,甲沿着 的路径行走至 ,乙沿着 的路径行走至 ,丙沿着 的路径行走至 .若三名同学行走的速度都相同,则他们到达各自的目的地的先后顺序(由先至后)是
A. 甲乙丙 B. 甲丙乙 C. 乙丙甲 D. 丙甲乙
12. 如图,正方形 中, 为边 上一动点,延长 至 ,使 ,连接 ,延长 与 相交于 ,下列结论正确的个数为
;;;.
A. B. C. D.
二、填空题(共6小题;共18分)
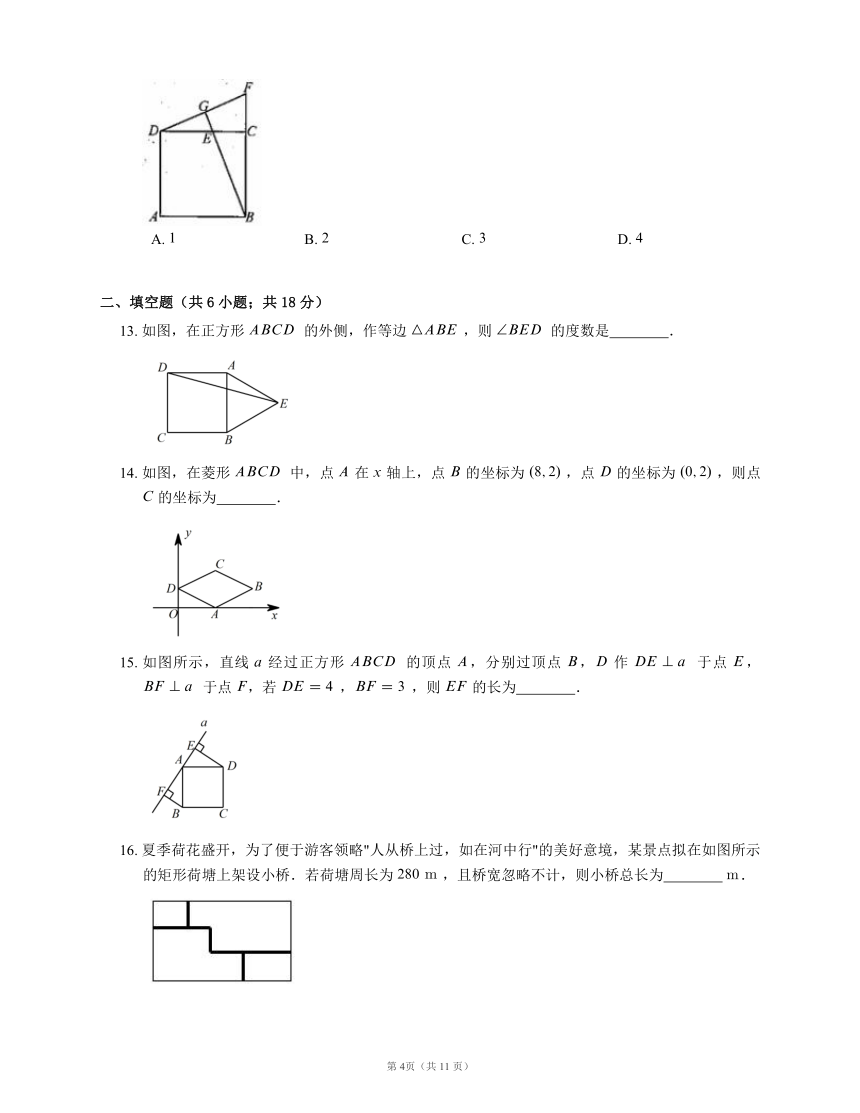
13. 如图,在正方形 的外侧,作等边 ,则 的度数是 ?.
14. 如图,在菱形 中,点 在 轴上,点 的坐标为 ,点 的坐标为 ,则点 的坐标为 ?.
15. 如图所示,直线 经过正方形 的顶点 ,分别过顶点 , 作 于点 , 于点 ,若 ,,则 的长为 ?.
16. 夏季荷花盛开,为了便于游客领略"人从桥上过,如在河中行"的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘周长为 ,且桥宽忽略不计,则小桥总长为 ? .
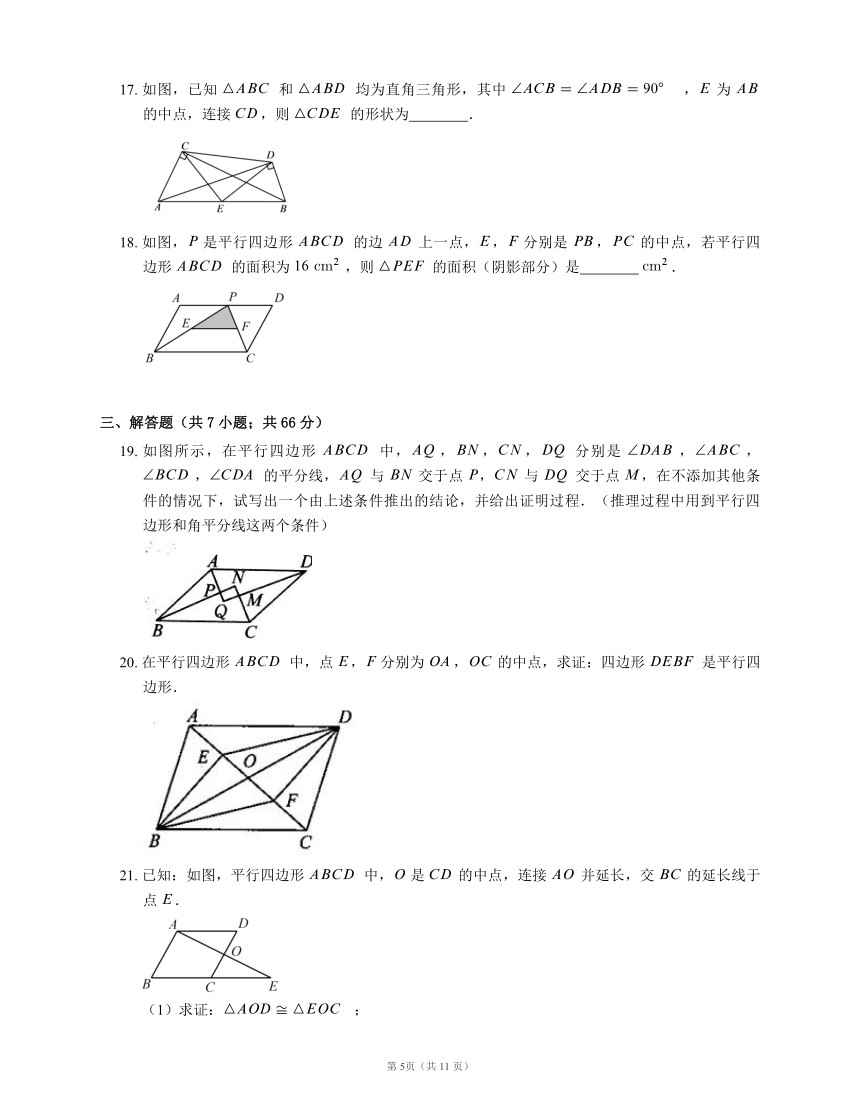
17. 如图,已知 和 均为直角三角形,其中 , 为 的中点,连接 ,则 的形状为 ?.
18. 如图, 是平行四边形 的边 上一点,, 分别是 , 的中点,若平行四边形 的面积为 ,则 的面积(阴影部分)是 ? .
三、解答题(共7小题;共66分)
19. 如图所示,在平行四边形 中,,,, 分别是 ,,, 的平分线, 与 交于点 , 与 交于点 ,在不添加其他条件的情况下,试写出一个由上述条件推出的结论,并给出证明过程.(推理过程中用到平行四边形和角平分线这两个条件)
20. 在平行四边形 中,点 , 分别为 , 的中点,求证:四边形 是平行四边形.
21. 已知:如图,平行四边形 中, 是 的中点,连接 并延长,交 的延长线于点 .
(1)求证:;
(2)连接 ,,当 ? 时,四边形 是正方形?请说明理由.
22. 如图,在 中, 是 边上的中线, 是 的中点,过点 作 的平行线交 的延长线于点 ,连接 .
(1)求证:.
(2)若 ,试判断四边形 的形状,并证明你的结论.
23. 如图,在正方形 中,对角线 , 相交于点 ,, 分别在 , 上,且 ,连接 ,, 的延长线交 于点 .求证:.
24. 如图,四边形 是菱形,对角线 , 相交于点 , 于点 ,连接 ,求 证:.
25. 已知:如图,在矩形 中,, 分别是边 , 的中点,, 分别是线段 , 的中点.
(1)求证:;
(2)判断四边形 是什么特殊四边形,并证明你的结论;
(3)当 ? 时,四边形 是正方形(只写结论,不需证明).
答案
第一部分
1. D 【解析】只有②③两块角的两边互相平行,角的两边的延长线的交点就是平行四边形的顶点.
2. A
3. A
4. A
5. D
【解析】如图,连接 ,
由于 是 斜边上的中线,
所以 ,不管木杆如何滑动,它的长度不变,
也就是 是一个定值,点 就在以 为圆心的圆弧上,
那么中点 下落的路线是一段弧线.
6. A
7. C
8. C 【解析】 四边形 是平行四边形,
,,,
,
平分线为 ,
,
,
,
同理:,
,
.
9. B 【解析】,
.
在 和 中,
().
,(故①正确);
于点 , 于点 ,
.
,
四边形 是平行四边形.
,(故②正确);
,
.
.
,
四边形 是平行四边形,(故③正确);
由以上可得出:,,,
,, 等.(故 错误).
故正确的有 个.
10. D
【解析】 垂直平分 ,
,.
又 ,
,
所以四边形 为菱形.
如果 ,
那么 ,
则 ,能证明四边形 为正方形.
如果 ,
那么 ,
能证明四边形 为正方形.
如果 ,
那么 ,
能证明四边形 为正方形.
当 时,
可得 ,
此时 ,
则 ,不能证明四边形 为正方形.
11. B 【解析】 四边形 是正方形,
,.
甲行走的距离是 ;
乙行走的距离是 ;
丙行走的距离是 .
,
,.
在 中 ,
,.
甲比丙先到,丙比乙先到.
12. C
第二部分
13.
14.
15.
16.
17. 等腰三角形
18.
【解析】 平行四边形 的面积为 ,
,
, 分别是 , 的中点,
,且 ,
,
,即 ,
.
第三部分
19. 可得出 是直角三角形, 等,证明略.
20. 提示:利用对角线互相平分证明.
21. (1) 四边形 是平行四边形,
.
,.
又 ,
.
??????(2)
当 时,四边形 是正方形.
,
.
又 ,
四边形 是平行四边形.
,
,.
四边形 是平行四边形,
,.
.
平行四边形 是菱形.
,,
.
菱形 是正方形.
22. (1) 是 的中点,
.
,
,.
.
.
是 边上的中线,
,
.
??????(2) 四边形 是菱形.
由(1)知, .
,
四边形 是平行四边形.
又 ,
是直角三角形.
是 边上的中线,
.
平行四边形 是菱形.
23. 四边形 是正方形,
,,,.
在 与 中,
(),
.
,
,
,即 .
24. 四边形 是菱形,
,,
, ,
,
又 ,
.
在 中,,
在 中,,
.
25. (1) 四边形 是矩形,
,.
在 和 中,
.
??????(2) 四边形 是菱形.
理由:
,,
,.
同理可得 ,.
四边形 是平行四边形.
,
,
,
平行四边形 是菱形.
??????(3) .
第2页(共11 页)
一、选择题(共12小题;共36分)
1. 小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是
A. ①② B. ①④ C. ③④ D. ②③
2. 如图,在 中,, 是 的中线, 与 相交于点 ,点 , 分别是 , 的中点,连接 .若 ,,则四边形 的周长是
A. B. C. D.
3. 如图,菱形 中,对角线 , 相交于点 , 为 边中点,菱形 的周长为 ,则 的长等于
A. B. C. D.
4. 如图,平行四边形 中,,, 于点 ,则 等于
A. B. C. D.
5. 木杆 斜靠在墙壁上,当木杆的上端 沿墙壁 竖直下滑时,木杆的底端 也随之沿着射线 方向滑动.下列图中用虚线画出木杆中点 随之下落的路线,其中正确的是
A. B.
C. D.
6. 如图,在 中,,, 平分 , 点是 的中点,若 ,则 的长为
A. B. C. D.
7. 如图,点 是等边三角形 内任意一点,过点 的直线中,,,,如果等边三角形 的边长是 ,那么
A. B. C. D.
8. 如图,在平行四边形 中,,, 的平分线交 于 ,交 的延长线于 ,则 的值等于
A. B. C. D.
9. 如图所示,四边形 中,,对角线 , 相交于点 , 于点 , 于点 ,连接 ,,若 ,则下列结论:① ;② ;③四边形 是平行四边形;④图中共有四对全等三角形.其中正确结论的个数是
A. B. C. D.
10. 如图,在 中,, 的垂直平分线 交 于点 ,交 于点 ,且 .添加一个条件,仍不能证明四边形 为正方形的是
A. B. C. D.
11. 如图, 是正方形场地,点 在 的延长线上, 与 相交于点 .有甲、乙、丙三名同学同时从点 出发,甲沿着 的路径行走至 ,乙沿着 的路径行走至 ,丙沿着 的路径行走至 .若三名同学行走的速度都相同,则他们到达各自的目的地的先后顺序(由先至后)是
A. 甲乙丙 B. 甲丙乙 C. 乙丙甲 D. 丙甲乙
12. 如图,正方形 中, 为边 上一动点,延长 至 ,使 ,连接 ,延长 与 相交于 ,下列结论正确的个数为
;;;.
A. B. C. D.
二、填空题(共6小题;共18分)
13. 如图,在正方形 的外侧,作等边 ,则 的度数是 ?.
14. 如图,在菱形 中,点 在 轴上,点 的坐标为 ,点 的坐标为 ,则点 的坐标为 ?.
15. 如图所示,直线 经过正方形 的顶点 ,分别过顶点 , 作 于点 , 于点 ,若 ,,则 的长为 ?.
16. 夏季荷花盛开,为了便于游客领略"人从桥上过,如在河中行"的美好意境,某景点拟在如图所示的矩形荷塘上架设小桥.若荷塘周长为 ,且桥宽忽略不计,则小桥总长为 ? .
17. 如图,已知 和 均为直角三角形,其中 , 为 的中点,连接 ,则 的形状为 ?.
18. 如图, 是平行四边形 的边 上一点,, 分别是 , 的中点,若平行四边形 的面积为 ,则 的面积(阴影部分)是 ? .
三、解答题(共7小题;共66分)
19. 如图所示,在平行四边形 中,,,, 分别是 ,,, 的平分线, 与 交于点 , 与 交于点 ,在不添加其他条件的情况下,试写出一个由上述条件推出的结论,并给出证明过程.(推理过程中用到平行四边形和角平分线这两个条件)
20. 在平行四边形 中,点 , 分别为 , 的中点,求证:四边形 是平行四边形.
21. 已知:如图,平行四边形 中, 是 的中点,连接 并延长,交 的延长线于点 .
(1)求证:;
(2)连接 ,,当 ? 时,四边形 是正方形?请说明理由.
22. 如图,在 中, 是 边上的中线, 是 的中点,过点 作 的平行线交 的延长线于点 ,连接 .
(1)求证:.
(2)若 ,试判断四边形 的形状,并证明你的结论.
23. 如图,在正方形 中,对角线 , 相交于点 ,, 分别在 , 上,且 ,连接 ,, 的延长线交 于点 .求证:.
24. 如图,四边形 是菱形,对角线 , 相交于点 , 于点 ,连接 ,求 证:.
25. 已知:如图,在矩形 中,, 分别是边 , 的中点,, 分别是线段 , 的中点.
(1)求证:;
(2)判断四边形 是什么特殊四边形,并证明你的结论;
(3)当 ? 时,四边形 是正方形(只写结论,不需证明).
答案
第一部分
1. D 【解析】只有②③两块角的两边互相平行,角的两边的延长线的交点就是平行四边形的顶点.
2. A
3. A
4. A
5. D
【解析】如图,连接 ,
由于 是 斜边上的中线,
所以 ,不管木杆如何滑动,它的长度不变,
也就是 是一个定值,点 就在以 为圆心的圆弧上,
那么中点 下落的路线是一段弧线.
6. A
7. C
8. C 【解析】 四边形 是平行四边形,
,,,
,
平分线为 ,
,
,
,
同理:,
,
.
9. B 【解析】,
.
在 和 中,
().
,(故①正确);
于点 , 于点 ,
.
,
四边形 是平行四边形.
,(故②正确);
,
.
.
,
四边形 是平行四边形,(故③正确);
由以上可得出:,,,
,, 等.(故 错误).
故正确的有 个.
10. D
【解析】 垂直平分 ,
,.
又 ,
,
所以四边形 为菱形.
如果 ,
那么 ,
则 ,能证明四边形 为正方形.
如果 ,
那么 ,
能证明四边形 为正方形.
如果 ,
那么 ,
能证明四边形 为正方形.
当 时,
可得 ,
此时 ,
则 ,不能证明四边形 为正方形.
11. B 【解析】 四边形 是正方形,
,.
甲行走的距离是 ;
乙行走的距离是 ;
丙行走的距离是 .
,
,.
在 中 ,
,.
甲比丙先到,丙比乙先到.
12. C
第二部分
13.
14.
15.
16.
17. 等腰三角形
18.
【解析】 平行四边形 的面积为 ,
,
, 分别是 , 的中点,
,且 ,
,
,即 ,
.
第三部分
19. 可得出 是直角三角形, 等,证明略.
20. 提示:利用对角线互相平分证明.
21. (1) 四边形 是平行四边形,
.
,.
又 ,
.
??????(2)
当 时,四边形 是正方形.
,
.
又 ,
四边形 是平行四边形.
,
,.
四边形 是平行四边形,
,.
.
平行四边形 是菱形.
,,
.
菱形 是正方形.
22. (1) 是 的中点,
.
,
,.
.
.
是 边上的中线,
,
.
??????(2) 四边形 是菱形.
由(1)知, .
,
四边形 是平行四边形.
又 ,
是直角三角形.
是 边上的中线,
.
平行四边形 是菱形.
23. 四边形 是正方形,
,,,.
在 与 中,
(),
.
,
,
,即 .
24. 四边形 是菱形,
,,
, ,
,
又 ,
.
在 中,,
在 中,,
.
25. (1) 四边形 是矩形,
,.
在 和 中,
.
??????(2) 四边形 是菱形.
理由:
,,
,.
同理可得 ,.
四边形 是平行四边形.
,
,
,
平行四边形 是菱形.
??????(3) .
第2页(共11 页)
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
