五年级下册数学课件-空间与几何(共17张PPT)
文档属性
| 名称 | 五年级下册数学课件-空间与几何(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-23 11:54:10 | ||
图片预览



文档简介
(共17张PPT)
“空间与几何”复习
《数学》五年级下册
湖北省十堰市郧阳区白桑九年一贯制学校
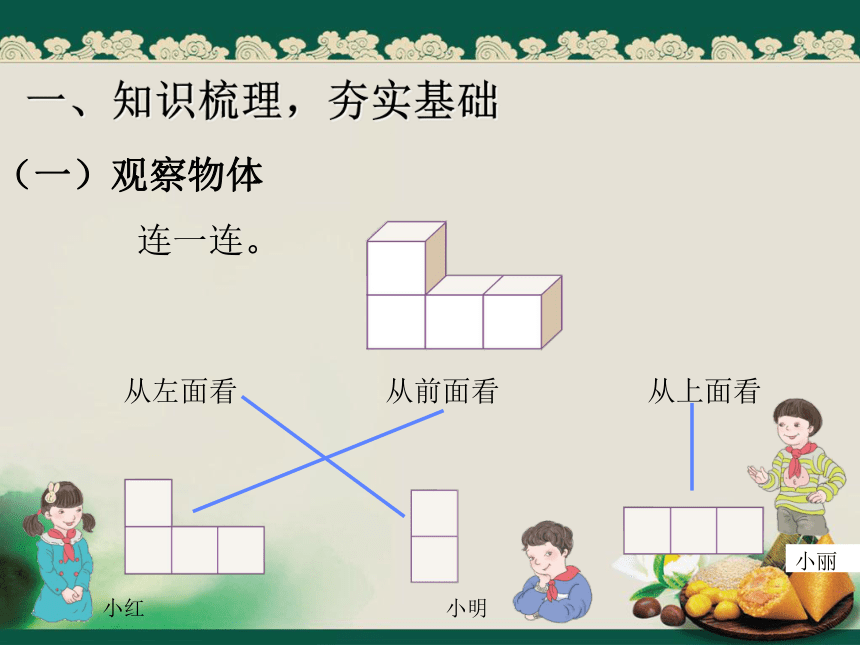
一、知识梳理,夯实基础
小明
小丽
小红
从前面看
从上面看
从左面看
连一连。
(一)观察物体
*
(一)观察物体
观察物体(三)
认识到从不同位置观察到物体的形状是不同的。
能辨认从前面、左面、上面观察到的立体图形的形状。
(一)观察物体
下面3个图形都是由棱长1cm的小正方体摆成的。
(1)下面的图形是聪聪从上面看到的,它们分别是从哪个图形
的上面看到的?将序号写在括号中。
③
②
①
(2)①、②、③的体积分别是多少?
顺
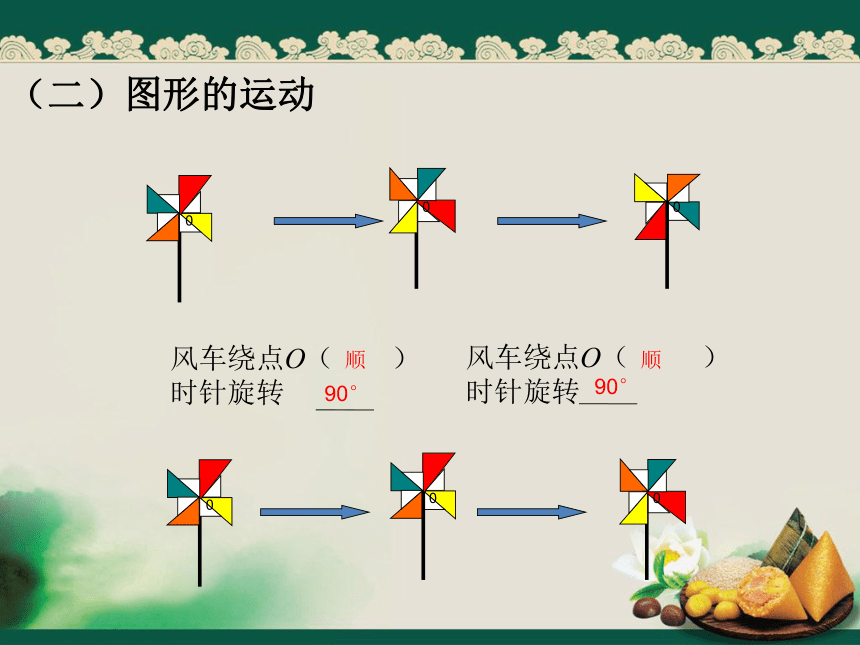
(二)图形的运动
风车绕点O( )
时针旋转
风车绕点O( )
时针旋转
顺
90°
90°
0
0
0
0
0
0
*
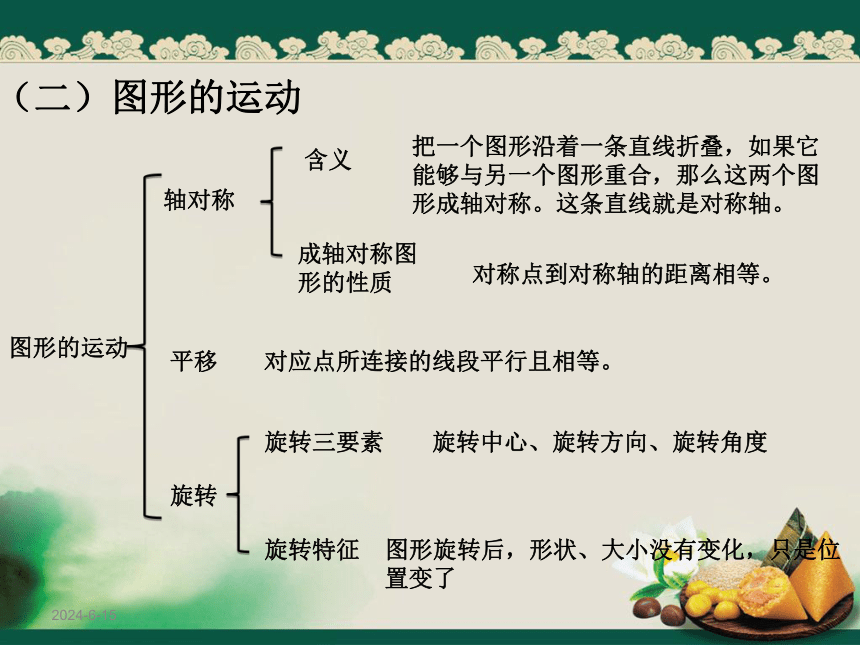
(二)图形的运动
把一个图形沿着一条直线折叠,如果它能够与另一个图形重合,那么这两个图形成轴对称。这条直线就是对称轴。
图形的运动
对称点到对称轴的距离相等。
对应点所连接的线段平行且相等。
轴对称
平移
旋转
含义
成轴对称图形的性质
旋转中心、旋转方向、旋转角度
旋转三要素
旋转特征
图形旋转后,形状、大小没有变化,只是位置变了
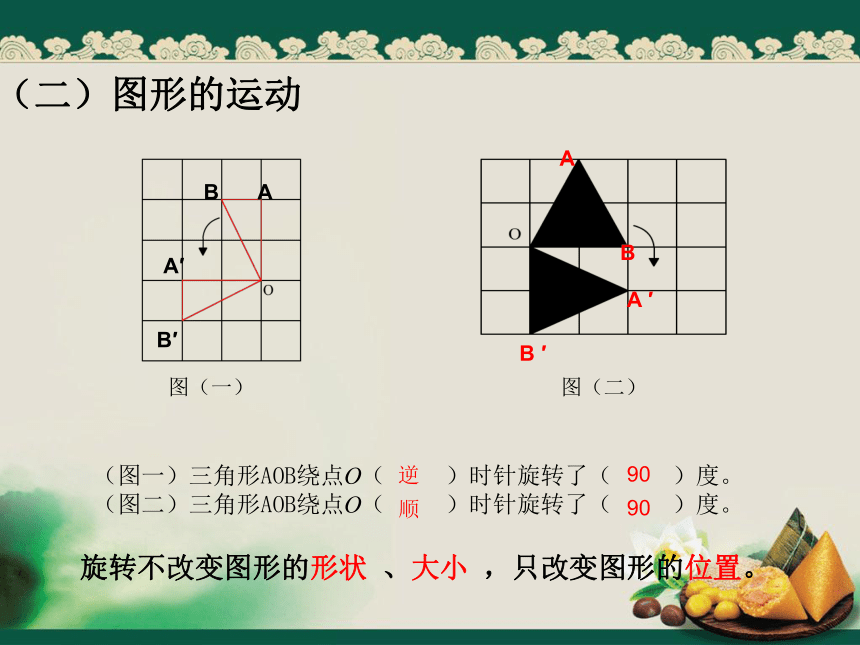
(图一)三角形AOB绕点O( )时针旋转了( )度。
(图二)三角形AOB绕点O( )时针旋转了( )度。
逆
90
顺
90
旋转不改变图形的形状 、大小 ,只改变图形的位置。
图(一)
(二)图形的运动
图(二)
A
B
A′
B′
A
B ′
B
A ′
*
异同点
表面积
相同点
不同点
体 积
容 积
(三)长方体和正方体
长方体和正方体
6个面、12条棱、8个顶点
长方体
正方体
6个面都是正方形且完全相同,棱长都相等
6个面都是长方形(有时相对的两个面是正方形);相对面完全相同;相对棱长度相等
长方体
正方体
正方体
正方体
长方体
长方体
2
V= abh=sh
S =(长×高+长×宽+宽×高)×2=2(ab+ah+bh)
S =6×棱长×棱长=6a
V=
V=abh
V=a?
含义:物体所占空间的大小,叫做物体的体积。
一个容器所能容纳物体的体积,叫做这个容器的容积。
(三)长方体和正方体
●
a
h
b
单位:厘米
长方体6个面的总面积,就是长方体的表面积。
1.长方体表面积的含义
长方体每个面的面积是多少呢?
前、后面:长 ×高
上、下面:长 ×宽
侧面:宽×高
(三)长方体和正方体
2.正方体表面积的含义
正方体展开图的每个面都是正方形,边长就是正方形的棱长,每个面的面积都等于棱长乘棱长。
a
a
S=6×棱长×棱长
注意事项
1.正确应用公式:求表面积用表面积公式,求体积要用体积公式。
2.单位统一。
3.在求与表面积有关实际问题时,要根据实际情况进行计算。
4.正方体是特殊的长方体。
二、知识应用,提高能力
1. 3.5ml=( )cm?
450dm?=( ) m?
2.正方体的棱长扩大到原来的5倍,它的一个面的面积扩大到原来的( )倍,它的表面积扩大到原来的( )倍,它的体积扩大到原来的( )倍。
3.正方形是轴对称图形,它有4条对称轴。( )
0.45
3.5
25
25
125
√
4.一块长方形铁皮,长40cm,宽30cm,像下图这样从4个角各剪掉一个边长为5厘米的正方形,然后做成盒子。这个盒子用了多少铁皮?它的容积是多少升?
容积:(40-5×2)×(30-5×2)×5=3000(cm?)
3000cm?=3L
答:这个盒子用了1700平方厘米铁皮。这个盒子的容积是3升。
长:40-5×2=30(㎝)
宽:30 -5×2=20(㎝)
高:5cm
表面积:
( 30×20+30×5+20×5)×2=1700(cm?)
5.把下图的长方体木块平均分成三块后,木块的棱长增加多少厘米?
5×8+ 10×8
= 40+80
= 120(厘米)
答:木块的棱长增加120厘米。
8
2.8
4
6
6.一只长方体的玻璃缸,长8分米,宽6分米,高4分米,水深2.8分米。如果投入一块棱长为4分米的正方体铁块(如下图),缸里的水溢出多少升?
求缸里的水溢出多少就是求正方体铁块的体积比长方体玻璃钢还能容纳的物体体积多多少。
4 ×4×4 - 8×6×(4 - 2.8)
=64 - 57.6
=6.4(dm?)
= 6.4 (L)
答:缸里的水溢出6.4升。
三、知识小结,加深印象
通过本节课的复习,你有新的收获吗?
“空间与几何”复习
《数学》五年级下册
湖北省十堰市郧阳区白桑九年一贯制学校
一、知识梳理,夯实基础
小明
小丽
小红
从前面看
从上面看
从左面看
连一连。
(一)观察物体
*
(一)观察物体
观察物体(三)
认识到从不同位置观察到物体的形状是不同的。
能辨认从前面、左面、上面观察到的立体图形的形状。
(一)观察物体
下面3个图形都是由棱长1cm的小正方体摆成的。
(1)下面的图形是聪聪从上面看到的,它们分别是从哪个图形
的上面看到的?将序号写在括号中。
③
②
①
(2)①、②、③的体积分别是多少?
顺
(二)图形的运动
风车绕点O( )
时针旋转
风车绕点O( )
时针旋转
顺
90°
90°
0
0
0
0
0
0
*
(二)图形的运动
把一个图形沿着一条直线折叠,如果它能够与另一个图形重合,那么这两个图形成轴对称。这条直线就是对称轴。
图形的运动
对称点到对称轴的距离相等。
对应点所连接的线段平行且相等。
轴对称
平移
旋转
含义
成轴对称图形的性质
旋转中心、旋转方向、旋转角度
旋转三要素
旋转特征
图形旋转后,形状、大小没有变化,只是位置变了
(图一)三角形AOB绕点O( )时针旋转了( )度。
(图二)三角形AOB绕点O( )时针旋转了( )度。
逆
90
顺
90
旋转不改变图形的形状 、大小 ,只改变图形的位置。
图(一)
(二)图形的运动
图(二)
A
B
A′
B′
A
B ′
B
A ′
*
异同点
表面积
相同点
不同点
体 积
容 积
(三)长方体和正方体
长方体和正方体
6个面、12条棱、8个顶点
长方体
正方体
6个面都是正方形且完全相同,棱长都相等
6个面都是长方形(有时相对的两个面是正方形);相对面完全相同;相对棱长度相等
长方体
正方体
正方体
正方体
长方体
长方体
2
V= abh=sh
S =(长×高+长×宽+宽×高)×2=2(ab+ah+bh)
S =6×棱长×棱长=6a
V=
V=abh
V=a?
含义:物体所占空间的大小,叫做物体的体积。
一个容器所能容纳物体的体积,叫做这个容器的容积。
(三)长方体和正方体
●
a
h
b
单位:厘米
长方体6个面的总面积,就是长方体的表面积。
1.长方体表面积的含义
长方体每个面的面积是多少呢?
前、后面:长 ×高
上、下面:长 ×宽
侧面:宽×高
(三)长方体和正方体
2.正方体表面积的含义
正方体展开图的每个面都是正方形,边长就是正方形的棱长,每个面的面积都等于棱长乘棱长。
a
a
S=6×棱长×棱长
注意事项
1.正确应用公式:求表面积用表面积公式,求体积要用体积公式。
2.单位统一。
3.在求与表面积有关实际问题时,要根据实际情况进行计算。
4.正方体是特殊的长方体。
二、知识应用,提高能力
1. 3.5ml=( )cm?
450dm?=( ) m?
2.正方体的棱长扩大到原来的5倍,它的一个面的面积扩大到原来的( )倍,它的表面积扩大到原来的( )倍,它的体积扩大到原来的( )倍。
3.正方形是轴对称图形,它有4条对称轴。( )
0.45
3.5
25
25
125
√
4.一块长方形铁皮,长40cm,宽30cm,像下图这样从4个角各剪掉一个边长为5厘米的正方形,然后做成盒子。这个盒子用了多少铁皮?它的容积是多少升?
容积:(40-5×2)×(30-5×2)×5=3000(cm?)
3000cm?=3L
答:这个盒子用了1700平方厘米铁皮。这个盒子的容积是3升。
长:40-5×2=30(㎝)
宽:30 -5×2=20(㎝)
高:5cm
表面积:
( 30×20+30×5+20×5)×2=1700(cm?)
5.把下图的长方体木块平均分成三块后,木块的棱长增加多少厘米?
5×8+ 10×8
= 40+80
= 120(厘米)
答:木块的棱长增加120厘米。
8
2.8
4
6
6.一只长方体的玻璃缸,长8分米,宽6分米,高4分米,水深2.8分米。如果投入一块棱长为4分米的正方体铁块(如下图),缸里的水溢出多少升?
求缸里的水溢出多少就是求正方体铁块的体积比长方体玻璃钢还能容纳的物体体积多多少。
4 ×4×4 - 8×6×(4 - 2.8)
=64 - 57.6
=6.4(dm?)
= 6.4 (L)
答:缸里的水溢出6.4升。
三、知识小结,加深印象
通过本节课的复习,你有新的收获吗?
