浙江省台州市第一中学2019-2020学年高二上学期期中考试数学试题
文档属性
| 名称 | 浙江省台州市第一中学2019-2020学年高二上学期期中考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 731.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-22 21:39:36 | ||
图片预览



文档简介
2019学年台州一中高二上期中
一、选择题:每小题4分,共40分
1.点A(1,2)到直线l:3x﹣4y﹣1=0的距离为( )
A. B. C.4 D.6
2.设m,n是空间中不同的直线,α,β是空间中不同的平面,则下列说法正确的是( )
A.α∥β,m?α,则m∥β
B.m?α,n?β,α∥β,则m∥n
C.m∥n,n?α,则m∥α
D.m?α,n?β,m∥β,n∥α,则α∥β
3.过两点A(4,y),B(2,﹣3)的直线的倾斜角为45°,则y=( )
A. B. C.﹣1 D.1
4.将半径为1,圆心角为的扇形围成一个圆锥,则该圆锥的体积为( )
A. B. C. D.
5.下列说法中正确的是( )
A.若一个命题的逆命题为真,则它的逆否命题一定为真
B.若一个命题的否命题为真,则它的逆否命题一定为真
C.“若a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0”
D.“若a2+b2=0,则a,b全为0”的逆否命题是“若a,b不全为0,则a2+b2≠0”
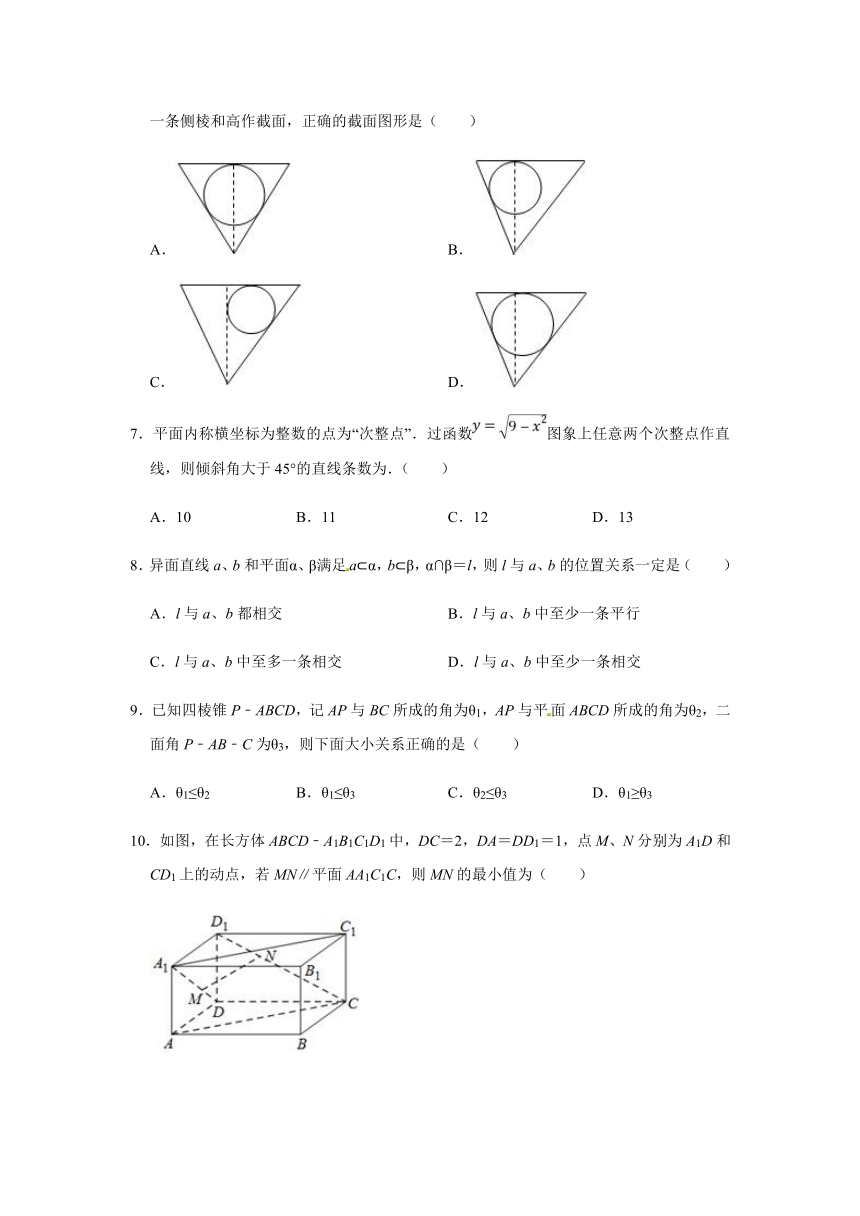
6.在一个倒置的正三棱锥容器内放入一个钢球,钢球恰与棱锥的四个面都接触,过棱锥的一条侧棱和高作截面,正确的截面图形是( )
A. B.
C. D.
7.平面内称横坐标为整数的点为“次整点”.过函数图象上任意两个次整点作直线,则倾斜角大于45°的直线条数为.( )
A.10 B.11 C.12 D.13
8.异面直线a、b和平面α、β满足a?α,b?β,α∩β=l,则l与a、b的位置关系一定是( )
A.l与a、b都相交 B.l与a、b中至少一条平行
C.l与a、b中至多一条相交 D.l与a、b中至少一条相交
9.已知四棱锥P﹣ABCD,记AP与BC所成的角为θ1,AP与平面ABCD所成的角为θ2,二面角P﹣AB﹣C为θ3,则下面大小关系正确的是( )
A.θ1≤θ2 B.θ1≤θ3 C.θ2≤θ3 D.θ1≥θ3
10.如图,在长方体ABCD﹣A1B1C1D1中,DC=2,DA=DD1=1,点M、N分别为A1D和CD1上的动点,若MN∥平面AA1C1C,则MN的最小值为( )
A. B. C. D.
二、填空题:11-14每空3分,15-17每空4分,共36分
11.在空间直角坐标系中,已知点A(1,0,2)与点B(1,﹣3,1),则|AB|= ,若在z轴上有一点M满足|MA|=|MB|,则点M坐标为 .
12.已知直线l1:(m﹣1)x+6y+2=0,l2:x+my+1=0,m为常数,若l1⊥l2,则m的值为 ,若l1∥l2,则m的值为 .
13.如图,P为△ABC所在平面外一点,PA=PB=PC=1,∠APB=∠BPC=60°,∠APC=90°,若G为△ABC的重心,则|PG|长为 ,异面直线PA与BC所成角的余弦值为 .
14.若圆O:x2+y2=r2(r>0)与圆C:x2+y2+ax+by﹣7=0(a,b,r为常数),关于直线x﹣y+2=0对称,则a的值为 ,r的值为 .
15.如图,正四棱锥P﹣ABCD的侧棱长为4,侧面的顶角均30°,过点A作一截面与PB、PC、PD分别相交于E、F、G,则四边形AEFG周长的最小值为 .
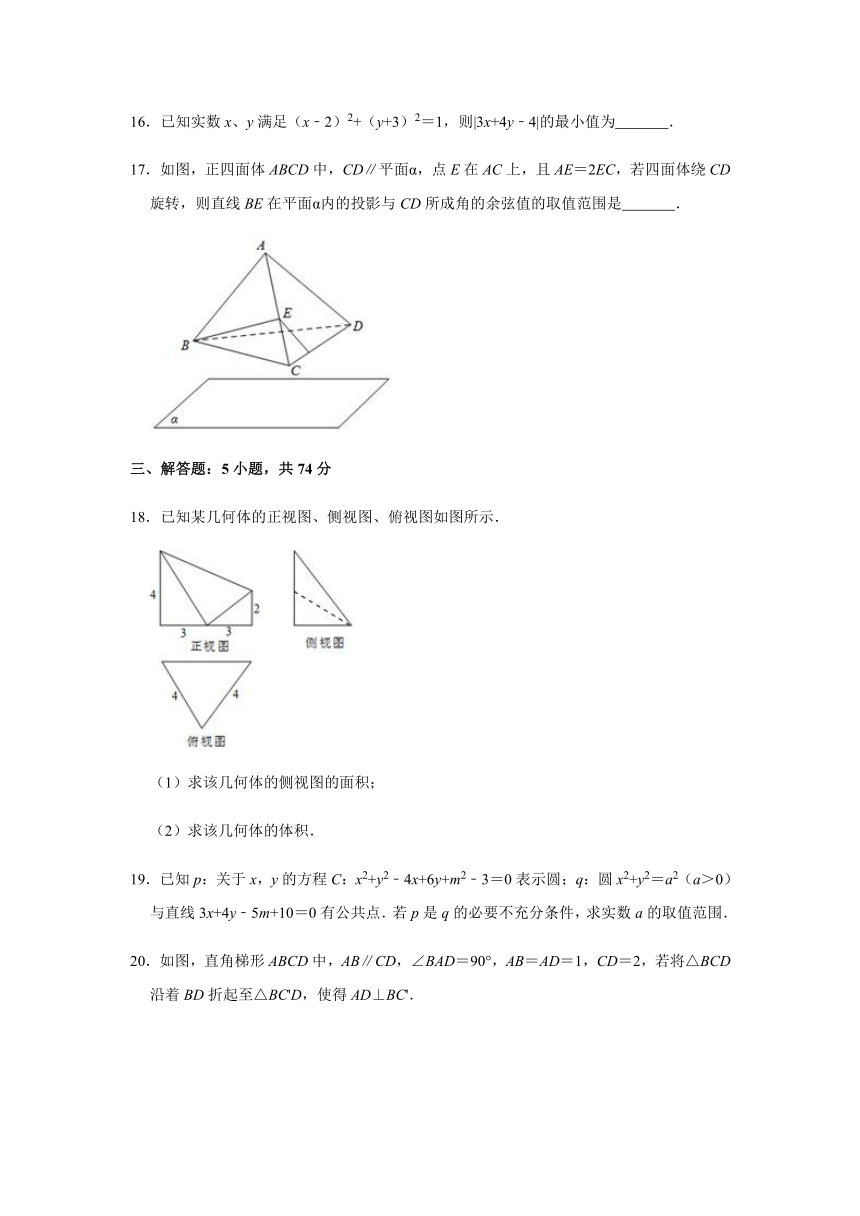
16.已知实数x、y满足(x﹣2)2+(y+3)2=1,则|3x+4y﹣4|的最小值为 .
17.如图,正四面体ABCD中,CD∥平面α,点E在AC上,且AE=2EC,若四面体绕CD旋转,则直线BE在平面α内的投影与CD所成角的余弦值的取值范围是 .
三、解答题:5小题,共74分
18.已知某几何体的正视图、侧视图、俯视图如图所示.
(1)求该几何体的侧视图的面积;
(2)求该几何体的体积.
19.已知p:关于x,y的方程C:x2+y2﹣4x+6y+m2﹣3=0表示圆;q:圆x2+y2=a2(a>0)与直线3x+4y﹣5m+10=0有公共点.若p是q的必要不充分条件,求实数a的取值范围.
20.如图,直角梯形ABCD中,AB∥CD,∠BAD=90°,AB=AD=1,CD=2,若将△BCD沿着BD折起至△BC'D,使得AD⊥BC'.
(1)求证:平面C'BD⊥平面ABD;
(2)求C'D与平面ABC'所成角的正弦值;
(3)M为BD中点,求二面角M﹣AC'﹣B的余弦值.
21.已知圆C过点A(2,6),且与直线l1:x+y﹣10=0相切于点B(6,4).
(1)求圆C的方程;
(2)过点P(6,24)的直线l2与圆C交于M,N两点,若△CMN为直角三角形,求直线l2的方程;
(3)在直线l3:y=x﹣2上是否存在一点Q,过Q向圆C引两条切线,切点为E,F,使△QEF为正三角形,若存在,求出点Q坐标,若不存在,说明理由.
22.如图,三棱柱ABC﹣A'B'C',AC=2,BC=4,∠ACB=120°,∠ACC'=90°,且平面AB'C⊥平面ABC,二面角A'﹣AC﹣B'为30°,E、F分别为A'C、B'C'的中点.
(1)求证:EF∥平面AB'C;
(2)求B'到平面ABC的距离;
(3)求二面角A﹣BB'﹣C'的余弦值.
一、选择题:每小题4分,共40分
1.B
2.A
3.C
4.B
5.D
6.B
7.B
8.D
9.C
10.B
二、填空题:11-14每空3分,15-17每空4分,共36分
11.,(0,0,﹣3).
12.
13. ;0.
14. 4,.
15.4.
16. 5.
17. [0,].
三、解答题:5小题,共74分
18.(1)由三视图知该几何体的侧视图是高为4,
底为的直角三角形,
所以侧视图的面积为S侧视图42.
(2)由三视图知该几何体是四棱锥,如图所示;
根据三视图中数据,计算该四棱锥的体积为
V四棱锥(2+4)×66.
19.∵p:关于x,y的方程C:x2+y2﹣4x+6y+m2﹣3=0表示圆;∴(x﹣2)2+(y+3)2=16﹣m2表示圆,即16﹣m2>0,∴p?﹣4<m<4;
∵q:圆x2+y2=a2(a>0)与直线3x+4y﹣5m+10=0有公共点.∴da,a>0;解得,q?2﹣a≤m≤2+a;
∵p是q的必要不充分条件,∴q?p,但p推不出q,∴,解得,a<2;
故实数a的取值范围是(﹣∞,2).
20.(1)过点B作DC的垂线交DC于点E,得CE=DE=1,BE=1,∴BC,
又AB=AD=1,∴BD,∴BC⊥BD,∴BC'⊥BD
又BC'⊥AD,且AD∩BD=D,AD、BD?平面ABD
∴BC'⊥平面ABD,又BC'?平面C'BD,∴平面C'BD⊥平面ABD;
(2)由(1)BC'⊥平面ABD可知:平面ABC'⊥平面ABD,
又AD⊥AB,平面ABC'∩平面ABD=AB,∴AD⊥平面ABC',
∴C'D与平面ABC'所成角为∠DC'A,
由(1)BC'⊥平面ABD可知:BC'⊥AB,∴AC',∴DC'=2,
∴sin∠DC'A,即C'D与平面ABC'所成角的正弦值为;
(3)以A为原点,AD、AB所在直线分别为x轴、y轴建立如图所示的空间直角坐标系,
由(1)BC'⊥平面ABD可知,A(0,0,0),B(0,1,0),C'(0,1,),D(1,0,0)
又M为BD的中点,∴M(),
∴,,,
∴平面MAC'的一个法向量,平面BAC'的一个法向量,
∴,
由图可知二面角M﹣AC'﹣B的大小为锐角,
∴二面角M﹣AC'﹣B的余弦值为.
21.(1)设圆心C(a,b),由题意:CA2=CB2得,(a﹣2)2+(b﹣6)2=(a﹣6)2+(b﹣4)2?2a﹣b﹣3=0①,
CB⊥l1,1②,
由①②得,a=1,b=﹣1,
即圆心C(1,﹣1),半径r=CA5,
所以圆C的方程:(x﹣1)2+(y+1)2=50.
(2).使△CMN为直角三角形,CM=CN,则∠MCN=90°,MNr=10,
∴圆心到直线l2的距离为dMN=5,
设l2的斜率存在时设直线l2方程:y﹣24=k(x﹣6)?kx﹣y﹣6k+24=0,
∴d5?k,
所以直线l2的方程:y﹣24(x﹣6),
当l2的斜率不存在时即x=6,这时圆心到直线的距离为6﹣1=5,正好△CMN也是直角三角形,也符合条件;
所以,直线l2的方程:12x﹣5y+48=0或者x=6.
(3),假设在直线l3:y=x﹣2上是否存在一点Q(m,m﹣2),
要使△QEF为正三角形,
则Rt△CQE中,∠CQE=30°,CQ=2r,
∴(m﹣1)2+(m﹣2+1)2=(2)2,
∴a=11或﹣9
即点Q坐标(11,9)或(﹣9,﹣11).
22.(1)证明:∵三棱柱ABC﹣A'B'C'中,四边形ACC′A′是平行四边形,
AC′∩A′C=E,
∴E是AC′的中点,
∵F是B'C'的中点,∴EF∥AB′,
∵EF?平面AB'C,AC′?平面AB'C,
∴EF∥平面AB'C.
(2)解:过B′作B′H⊥平面ABC,交AC延长线于点H,
过点H作CC′平行线HM,交A′C′于点M,连结HB,
则∠MHB′是二面角A'﹣AC﹣B'的平面角,
∵AC=2,BC=4,∠ACB=120°,∠ACC'=90°,且平面AB'C⊥平面ABC,二面角A'﹣AC﹣B'为30°,
∴∠MHB′=∠BB′H=30°,∠BCH=60°,∴∠HBC=30°,∠BHC=90°,
∴CH,∴BH2,
∴B'到平面ABC的距离B′H6.
(3)解:以H为原点,HA为x轴,HB为y轴,HB′为z轴,建立空间直角坐标系,
A(4,0,0),B(0,2,0),B′(0,0,6),C′(2,﹣2,6),
(4,﹣2,0),(0,﹣2,6),(2,﹣4,6),
设平面ABB'的法向量(x,y,z),
则,取x,得(,2,),
设平面BB'C'的法向量(x,y,z),
则,取x,得(,1,),
设二面角A﹣BB'﹣C'的平面角为θ.
则cosθ.
∴二面角A﹣BB'﹣C'的余弦值为.
