2020春北师大版八下数学2.5一元一次不等式与一次函数课件(共20张PPT)
文档属性
| 名称 | 2020春北师大版八下数学2.5一元一次不等式与一次函数课件(共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-23 21:52:04 | ||
图片预览







文档简介
课件20张PPT。千里之行,始于足下
伟人之所以伟大,是因为他与别人共处逆境时,别人失去了信心,他却下决心实现自己的目标1.解不等式2x-5>0,并把他的解集在数轴上表示出来2.一次函数的图象是__________.它与x轴的交点坐标是 ,与y轴的交点 坐标是 ;要作一次函数的图象,只需_______点即可
3. 一次函数 y = 2x – 5它与x轴的交点坐标是 ,与y轴的交点 坐标是 。画出该函数是图像。 下面我们来探讨一下一元一次不等式与一次函数之间的关系北 师 大? 八 年 级《 数 学 ( 下 ) 》课首
北 师 大 ? 八 年 级 《 数 学 ( 下 ) 》2.5一元一次不等式与一次函数 通过作图、观察,进一步理解一元一次函数概念,并从“形”这个角度体会一元一次不等式与一次函数的内在联系;教学目标、重点、难点根据题意列函数关系式,并能把函数关系式与一元一次不等式联系起来作答. 体会 不等关系与函数、方程是紧密联系着一个整体。一元一次不等式2x-5>0与一次函数y=2x-5之间的关联数 一次函数y=2x-5研究的是 问题,即(x,y),有时会遇到横坐标x取哪些值时纵坐标y>0的问题。而当y>0时,有不等式 。 不等式2x-5>0研究的是 成立。 因为y=2x-5,所以x取哪些值时, 2x-5>0成立的问题就是x 成立的问题综上所述“关于函数值的 问题 ”可以转化为“关于x 的不等式的问题”
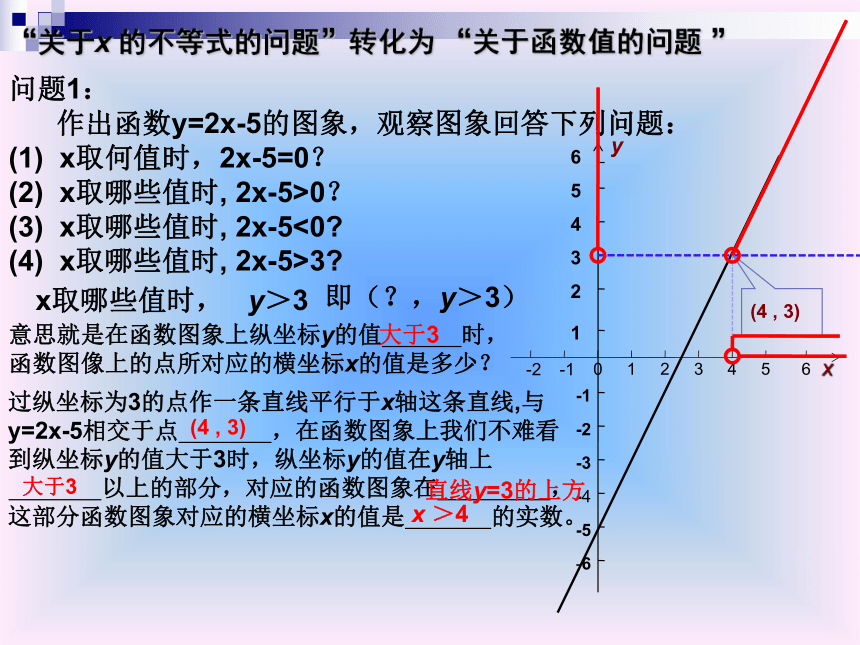
“关于x 的不等式的问题”可以转化为“关于函数值的 问题 ”形横坐标与纵坐标的取值2x-5>0x取哪些值时,2x-5>0x取哪些值时, y>0形解不等式2x-5>0的解集是x>2.5,把它表示在数轴上为:xy 对于一次函数y=2x-5,我们建立直角系,画出函数图象 求不等式2x-5>0的解集实质就是求x取何值时,2x-5>0,即就是一次函数中x取何值时, 。意思就是在函数图象上纵坐标y的值是 时,函数图像上的点所对应的横坐标x的值是多少? 在函数图象上我们不难看到纵坐标y的值是正数时即纵坐标y的值在y轴的 ,对应的函数图象在 ,这部分函数图象对应的横坐标x的值是 的实数。所以在函数图象上当x >2.5时,y>0。即上当x >2.5时, 2x-5>0。x取何值时,2x-5>0x轴的上方正半轴上x >2.5一元一次不等式2x-5>0与一次函数y=2x-5之间的关联y>0正数“关于x 的不等式的问题”转化为 “关于函数值的问题 ” 问题1:
作出函数y=2x-5的图象,观察图象回答下列问题:
(1) x取何值时,2x-5=0?
(2) x取哪些值时, 2x-5>0?
(3) x取哪些值时, 2x-5<0?
(4) x取哪些值时, 2x-5>3?x取何值时, y=0即(?,0) x取哪些值时, y>0即(?,y>0) x取哪些值时, y<0即(?,y <0) x取哪些值时, y>3即(?,y>3) 方法点睛:X轴上方的图象y值大于0问题1:
作出函数y=2x-5的图象,观察图象回答下列问题:
(1) x取何值时,2x-5=0?
(2) x取哪些值时, 2x-5>0?
(3) x取哪些值时, 2x-5<0?
(4) x取哪些值时, 2x-5>3?“关于x 的不等式的问题”转化为 “关于函数值的问题 ” xyx取哪些值时, y>3即(?,y>3) 意思就是在函数图象上纵坐标y的值 时,函数图像上的点所对应的横坐标x的值是多少? 过纵坐标为3的点作一条直线平行于x轴这条直线,与y=2x-5相交于点 ,在函数图象上我们不难看到纵坐标y的值大于3时,纵坐标y的值在y轴上
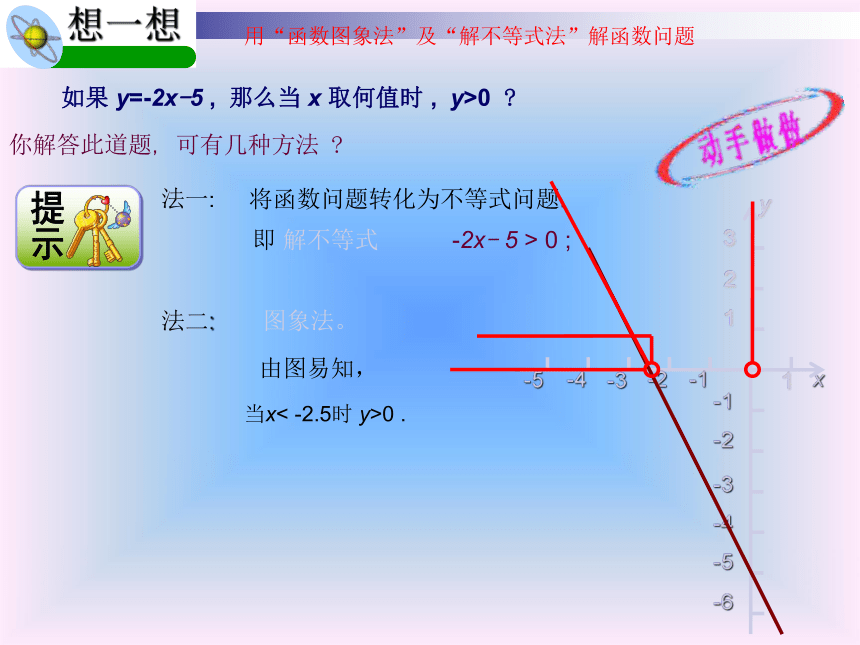
以上的部分,对应的函数图象在 ,这部分函数图象对应的横坐标x的值是 的实数。直线y=3的上方大于3 x >4大于3(4 , 3) 如果 y=-2x-5 , 那么当 x 取何值时 , y>0 ?你解答此道题, 可有几种方法 ? 将函数问题转化为不等式问题.即 解不等式-2x- 5 > 0 ;法二:图象法。当x< -2.5时 y>0 .用“函数图象法”及“解不等式法”解函数问题由上述讨易知: 函数、(方程) 不等式“关于一次函数的值的问题”
可变换成 “关于一次不等式的问题” ; 反过来, “关于一次不等式的问题”
可变换成 “关于一次函数的值的问题”。 因此, 我们既可以运用函数图象解不等式 ,也可以运用解不等式帮助研究函数问题 ,二者相互渗透 ,互相作用。 不等式与 函数 、方程 是紧密联系着的一个整体 。1、若y1=-x+3,y2=3x-4,试确定当x取何值时
(1)y1<y2?
(2)y1=y2?
(3)y1>y2?当x> 时, y1<y2当x< 时,你解答此道题, 可有几种方法 ? 图象法:解不等式法:y1=y2y1>y21、若y1=-x+3,y2=3x-4,试确定当x取何值时
(1)y1<y2?
(2)y1=y2?
(3)y1>y2?解不等式法:即:-x+3<3x-4即:-x+3=3x-4即:-x+3 < 3x-42.解不等式5x+4<2x+10解法1:原不等式化为3x -6<0,画出直线y = 3x -6(如图)所以不等式的解集为x<2函数图象法:解不等式法:解法2:画出直线y1 = 5x +4
y2 = 2x +10所以不等式的解集为x<2 兄弟俩赛跑,哥哥先让弟弟跑 9 米,然后自己才开始跑。
已知弟弟每秒跑 3 米,哥哥每秒跑 4 米。
列出函数关系式,画出函数图象,观察图象回答下列问题:(1) 何时弟弟跑在哥哥前面?P 20y哥= ,y弟= .(3) 何时哥哥跑在弟弟前面?(4) 谁先跑过 20米?谁先跑过 100米?9+3x4x答案:
(1) 从哥哥起跑开始 , 弟弟跑在哥哥前面;
(2) ) 从哥哥起跑开始,第 刚好追到弟在;
(3) 从哥哥起跑开始 , 哥哥跑弟弟在前面;
(3) 先跑过 20米, 先跑过 100米 .9s 前9s 后弟弟哥哥(2) 何时哥哥刚好追到弟弟?9s除了运用图象法解之外,
还可直接用不等式求解 兄弟俩赛跑,哥哥先让弟弟跑 9 米,然后自己才开始跑。
已知弟弟每秒跑 3 米,哥哥每秒跑 4 米。
列出函数关系式,画出函数图象,观察图象回答下列问题:(1) 何时弟弟跑在哥哥前面?P 20y哥= ,y弟= .(3) 何时哥哥跑在弟弟前面?(4) 谁先跑过 20米?谁先跑过 100米?9+3x4x答案:
(1) 从哥哥起跑开始 , 弟弟跑在哥哥前面;
(2) ) 从哥哥起跑开始,第 刚好追到弟在;
(3) 从哥哥起跑开始 , 哥哥跑弟弟在前面;
(3) 先跑过 20米, 先跑过 100米 .9s 前9s 后弟弟哥哥(2) 何时哥哥刚好追到弟弟?9s如图,l1反映了某产品的销售收入与销售量之间的关系, l2反映了该产品的销售成本与销售量之间的关系,当销售收入大于销售成本时,该产品才开始盈利。
(1)根据函数图象写出l1、 l2的函数解析式。
(2)试分析该产品的盈亏情况。4、甲、乙两辆摩托车从相距20km的A、B两地相向而行,图中l1、l2分别表示两辆摩托车离开A地的距离s(km)与行驶时间t(h)之间函数关系。
(1)哪辆摩托车的速度较快?
(2)经过多长时间,甲车行驶到A、B两地中点? 解答:(1)从图象中可知 故摩托车乙速度快。
(2)当s=10km时, 即经过0.3h时,甲车行驶到A、B两地的中点。 1、某单位准备和一个体车主或一国营出租车公司中
的一家签订月租车合同,设汽车每月行驶x 千米,个体车
主收费y1元,国营出租车公司收费为y2元,观察下列图象
可知(如图1-5-2),当x________时,选用个体车较合算.2、当自变量 x 的取值满足什么条件时,函数 y = 3x+8 的值满足下列条件?
y = 0 (2) y = -7
(3) y >0 (4) y < 2
一次函数(值)的变化对应着相应自变量的取值范围,
这个取值范围, 既可从一次函数的图象上直观看出(近似值),
也可通过解(方程)不等式而得到(精确值). 我们既可以运用函数图象解不等式 ,
也可以运用解不等式帮助研究函数问题 ,
二者相互渗透 ,互相作用。
不等式与 函数 、方程 是紧密联系着
的一个整体 。 作 业习 题 1.61、2 ;P20一元一次不等式
与一次函数P19
伟人之所以伟大,是因为他与别人共处逆境时,别人失去了信心,他却下决心实现自己的目标1.解不等式2x-5>0,并把他的解集在数轴上表示出来2.一次函数的图象是__________.它与x轴的交点坐标是 ,与y轴的交点 坐标是 ;要作一次函数的图象,只需_______点即可
3. 一次函数 y = 2x – 5它与x轴的交点坐标是 ,与y轴的交点 坐标是 。画出该函数是图像。 下面我们来探讨一下一元一次不等式与一次函数之间的关系北 师 大? 八 年 级《 数 学 ( 下 ) 》课首
北 师 大 ? 八 年 级 《 数 学 ( 下 ) 》2.5一元一次不等式与一次函数 通过作图、观察,进一步理解一元一次函数概念,并从“形”这个角度体会一元一次不等式与一次函数的内在联系;教学目标、重点、难点根据题意列函数关系式,并能把函数关系式与一元一次不等式联系起来作答. 体会 不等关系与函数、方程是紧密联系着一个整体。一元一次不等式2x-5>0与一次函数y=2x-5之间的关联数 一次函数y=2x-5研究的是 问题,即(x,y),有时会遇到横坐标x取哪些值时纵坐标y>0的问题。而当y>0时,有不等式 。 不等式2x-5>0研究的是 成立。 因为y=2x-5,所以x取哪些值时, 2x-5>0成立的问题就是x 成立的问题综上所述“关于函数值的 问题 ”可以转化为“关于x 的不等式的问题”
“关于x 的不等式的问题”可以转化为“关于函数值的 问题 ”形横坐标与纵坐标的取值2x-5>0x取哪些值时,2x-5>0x取哪些值时, y>0形解不等式2x-5>0的解集是x>2.5,把它表示在数轴上为:xy 对于一次函数y=2x-5,我们建立直角系,画出函数图象 求不等式2x-5>0的解集实质就是求x取何值时,2x-5>0,即就是一次函数中x取何值时, 。意思就是在函数图象上纵坐标y的值是 时,函数图像上的点所对应的横坐标x的值是多少? 在函数图象上我们不难看到纵坐标y的值是正数时即纵坐标y的值在y轴的 ,对应的函数图象在 ,这部分函数图象对应的横坐标x的值是 的实数。所以在函数图象上当x >2.5时,y>0。即上当x >2.5时, 2x-5>0。x取何值时,2x-5>0x轴的上方正半轴上x >2.5一元一次不等式2x-5>0与一次函数y=2x-5之间的关联y>0正数“关于x 的不等式的问题”转化为 “关于函数值的问题 ” 问题1:
作出函数y=2x-5的图象,观察图象回答下列问题:
(1) x取何值时,2x-5=0?
(2) x取哪些值时, 2x-5>0?
(3) x取哪些值时, 2x-5<0?
(4) x取哪些值时, 2x-5>3?x取何值时, y=0即(?,0) x取哪些值时, y>0即(?,y>0) x取哪些值时, y<0即(?,y <0) x取哪些值时, y>3即(?,y>3) 方法点睛:X轴上方的图象y值大于0问题1:
作出函数y=2x-5的图象,观察图象回答下列问题:
(1) x取何值时,2x-5=0?
(2) x取哪些值时, 2x-5>0?
(3) x取哪些值时, 2x-5<0?
(4) x取哪些值时, 2x-5>3?“关于x 的不等式的问题”转化为 “关于函数值的问题 ” xyx取哪些值时, y>3即(?,y>3) 意思就是在函数图象上纵坐标y的值 时,函数图像上的点所对应的横坐标x的值是多少? 过纵坐标为3的点作一条直线平行于x轴这条直线,与y=2x-5相交于点 ,在函数图象上我们不难看到纵坐标y的值大于3时,纵坐标y的值在y轴上
以上的部分,对应的函数图象在 ,这部分函数图象对应的横坐标x的值是 的实数。直线y=3的上方大于3 x >4大于3(4 , 3) 如果 y=-2x-5 , 那么当 x 取何值时 , y>0 ?你解答此道题, 可有几种方法 ? 将函数问题转化为不等式问题.即 解不等式-2x- 5 > 0 ;法二:图象法。当x< -2.5时 y>0 .用“函数图象法”及“解不等式法”解函数问题由上述讨易知: 函数、(方程) 不等式“关于一次函数的值的问题”
可变换成 “关于一次不等式的问题” ; 反过来, “关于一次不等式的问题”
可变换成 “关于一次函数的值的问题”。 因此, 我们既可以运用函数图象解不等式 ,也可以运用解不等式帮助研究函数问题 ,二者相互渗透 ,互相作用。 不等式与 函数 、方程 是紧密联系着的一个整体 。1、若y1=-x+3,y2=3x-4,试确定当x取何值时
(1)y1<y2?
(2)y1=y2?
(3)y1>y2?当x> 时, y1<y2当x< 时,你解答此道题, 可有几种方法 ? 图象法:解不等式法:y1=y2y1>y21、若y1=-x+3,y2=3x-4,试确定当x取何值时
(1)y1<y2?
(2)y1=y2?
(3)y1>y2?解不等式法:即:-x+3<3x-4即:-x+3=3x-4即:-x+3 < 3x-42.解不等式5x+4<2x+10解法1:原不等式化为3x -6<0,画出直线y = 3x -6(如图)所以不等式的解集为x<2函数图象法:解不等式法:解法2:画出直线y1 = 5x +4
y2 = 2x +10所以不等式的解集为x<2 兄弟俩赛跑,哥哥先让弟弟跑 9 米,然后自己才开始跑。
已知弟弟每秒跑 3 米,哥哥每秒跑 4 米。
列出函数关系式,画出函数图象,观察图象回答下列问题:(1) 何时弟弟跑在哥哥前面?P 20y哥= ,y弟= .(3) 何时哥哥跑在弟弟前面?(4) 谁先跑过 20米?谁先跑过 100米?9+3x4x答案:
(1) 从哥哥起跑开始 , 弟弟跑在哥哥前面;
(2) ) 从哥哥起跑开始,第 刚好追到弟在;
(3) 从哥哥起跑开始 , 哥哥跑弟弟在前面;
(3) 先跑过 20米, 先跑过 100米 .9s 前9s 后弟弟哥哥(2) 何时哥哥刚好追到弟弟?9s除了运用图象法解之外,
还可直接用不等式求解 兄弟俩赛跑,哥哥先让弟弟跑 9 米,然后自己才开始跑。
已知弟弟每秒跑 3 米,哥哥每秒跑 4 米。
列出函数关系式,画出函数图象,观察图象回答下列问题:(1) 何时弟弟跑在哥哥前面?P 20y哥= ,y弟= .(3) 何时哥哥跑在弟弟前面?(4) 谁先跑过 20米?谁先跑过 100米?9+3x4x答案:
(1) 从哥哥起跑开始 , 弟弟跑在哥哥前面;
(2) ) 从哥哥起跑开始,第 刚好追到弟在;
(3) 从哥哥起跑开始 , 哥哥跑弟弟在前面;
(3) 先跑过 20米, 先跑过 100米 .9s 前9s 后弟弟哥哥(2) 何时哥哥刚好追到弟弟?9s如图,l1反映了某产品的销售收入与销售量之间的关系, l2反映了该产品的销售成本与销售量之间的关系,当销售收入大于销售成本时,该产品才开始盈利。
(1)根据函数图象写出l1、 l2的函数解析式。
(2)试分析该产品的盈亏情况。4、甲、乙两辆摩托车从相距20km的A、B两地相向而行,图中l1、l2分别表示两辆摩托车离开A地的距离s(km)与行驶时间t(h)之间函数关系。
(1)哪辆摩托车的速度较快?
(2)经过多长时间,甲车行驶到A、B两地中点? 解答:(1)从图象中可知 故摩托车乙速度快。
(2)当s=10km时, 即经过0.3h时,甲车行驶到A、B两地的中点。 1、某单位准备和一个体车主或一国营出租车公司中
的一家签订月租车合同,设汽车每月行驶x 千米,个体车
主收费y1元,国营出租车公司收费为y2元,观察下列图象
可知(如图1-5-2),当x________时,选用个体车较合算.2、当自变量 x 的取值满足什么条件时,函数 y = 3x+8 的值满足下列条件?
y = 0 (2) y = -7
(3) y >0 (4) y < 2
一次函数(值)的变化对应着相应自变量的取值范围,
这个取值范围, 既可从一次函数的图象上直观看出(近似值),
也可通过解(方程)不等式而得到(精确值). 我们既可以运用函数图象解不等式 ,
也可以运用解不等式帮助研究函数问题 ,
二者相互渗透 ,互相作用。
不等式与 函数 、方程 是紧密联系着
的一个整体 。 作 业习 题 1.61、2 ;P20一元一次不等式
与一次函数P19
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
