人教版数学七年级下册 5.1.1 相交线 课件(共19张PPT)
文档属性
| 名称 | 人教版数学七年级下册 5.1.1 相交线 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 501.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-23 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
5.1.1 相交线
第五章 相交线与平行线
麻丘二中成春燕
情景导入
1
2
了解邻补角,对顶角的概念,能找出图形中一个角的邻补角和对顶角;
理解对顶角的性质,并会对其进行运用。
学习目标
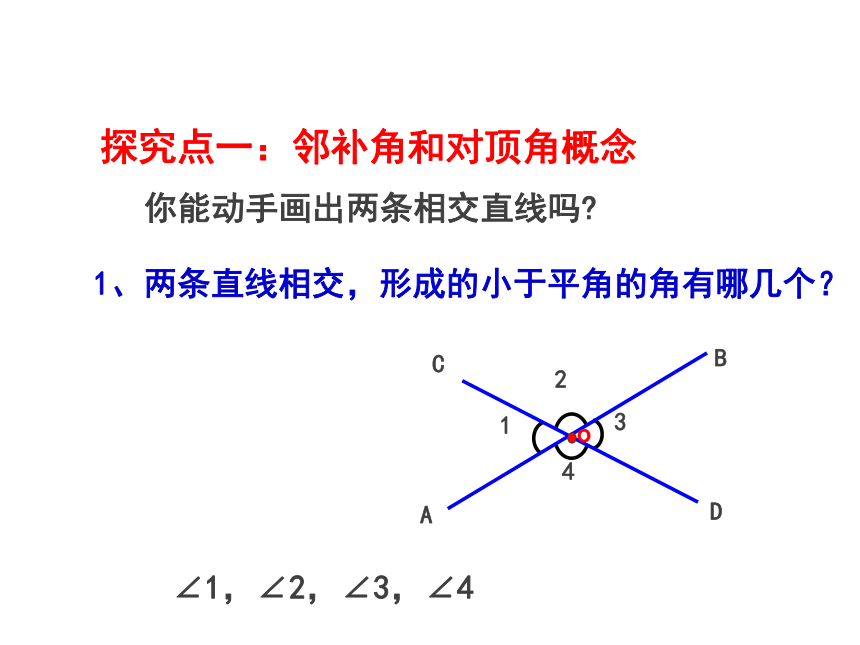
∠1,∠2,∠3,∠4
你能动手画出两条相交直线吗?
1、两条直线相交,形成的小于平角的角有哪几个?
探究点一:邻补角和对顶角概念
讲授新课
2、将这些角两两相配能得到几对角?
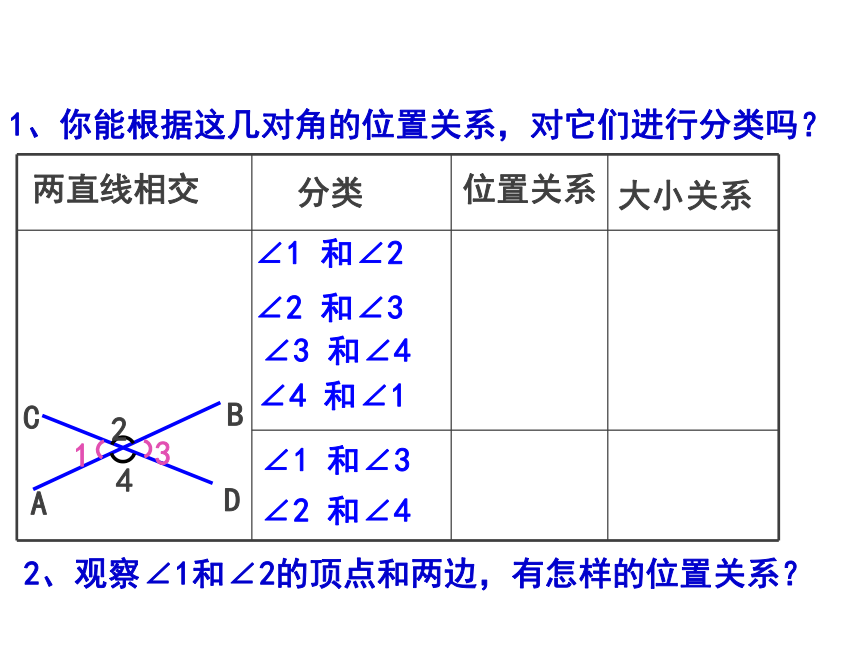
分类
两直线相交
∠1 和∠2
∠2 和∠3
∠1 和∠3
位置关系
大小关系
1、你能根据这几对角的位置关系,对它们进行分类吗?
∠3 和∠4
∠4 和∠1
∠2 和∠4
2、观察∠1和∠2的顶点和两边,有怎样的位置关系?
1
2
3
4
B
C
D
o
A
分类
邻补角
两直线相交
位置关系
大小关系
3、类比∠1和∠2,看∠1和∠3有怎样的位置关系?
∠1 和∠2
∠2 和∠
∠1 和∠3
3
∠3 和∠4
∠4 和∠1
∠2 和∠4
1
3
B
C
D
A
o
分类
邻补角
两直线相交
对顶角
位置关系
大小关系
4、你能写出邻补角∠1和∠2的大小关系式吗?
∠1+∠2=180°
∠2+∠3=180°
∠3+∠4=180°
∠4+∠1=180°
∠1 和∠2
∠2 和∠
∠1 和∠3
3
∠3 和∠4
∠4 和∠1
∠2 和∠4
探究点二:对顶角、邻补角的性质
分类
邻补角
两直线相交
对顶角
位置关系
大小关系
∠1+∠2=180°
∠2+∠3=180°
∠3+∠4=180°
∠4+∠1=180°
5、你能得到对顶角∠1和∠3的大小关系吗?
∠1 和∠2
∠2 和∠
∠1 和∠3
3
∠3 和∠4
∠4 和∠1
∠2 和∠4
∠ 2 +∠3= ,
4、你能得到对顶角∠1和∠3的大小关系吗?
∠2与∠3互补
∠1与∠2互补,
那么∠ 2 +∠1= ,
∠1= ∠3
180°
180°
由同角的补角相等可知
动动脑:为什么?
分类
邻补角
两直线相交
对顶角
位置关系
大小关系
∠1+∠2=180°
∠2+∠3=180°
∠3+∠4=180°
∠4+∠1=180°
邻补角、对顶角的位置关系和大小关系
∠1=∠3
∠2=∠4
∠1 和∠2
∠2 和∠
∠1 和∠3
3
∠3 和∠4
∠4 和∠1
∠2 和∠4
例1、如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数。
a
b
)
(
1
3
4
2
)
(
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°=140°
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°
变式:直线AB、CD相交与点O,∠AOC=40°,OE平分∠AOC,求∠DOE的度数。
解:∵OE平分∠AOC, 且∠AOC =40°
∴∠COE= ∠AOC=20°
∴∠DOE=180°-∠COE=120°
判断题:
1.如果两个角有公共顶点和一条公共边,而且这两角互为补角, 那么它们互为邻补角.
( × )
2.两条直线相交,如果它们所成的邻补角相等,那么一对对顶角就互补.
( √ )
课堂练习
填空题:
3.如图 ,直线AB、CD、EF相交于点O,∠BOE的对顶角是_______,∠COF 的邻补角是_____________
若∠AOC:∠AOE=2:3,∠EOD=130°,则∠BOC=__________
4.如图 ,直线AB、CD相交于点O,∠COE=90°,∠AOC=30°,∠FOB=90°, 则∠EOF=_____.
∠COF
∠COE和DOF
160°
150°
对顶角和邻补角各有什么特征?产生这两
类角的前提是什么?
2.对顶角有什么性质?这个性质是怎么推导
出来的?
3.两条直线相交形成的四个角中,有几对对
顶角?几对邻补角?
课堂小结
5.1.1 相交线
第五章 相交线与平行线
麻丘二中成春燕
情景导入
1
2
了解邻补角,对顶角的概念,能找出图形中一个角的邻补角和对顶角;
理解对顶角的性质,并会对其进行运用。
学习目标
∠1,∠2,∠3,∠4
你能动手画出两条相交直线吗?
1、两条直线相交,形成的小于平角的角有哪几个?
探究点一:邻补角和对顶角概念
讲授新课
2、将这些角两两相配能得到几对角?
分类
两直线相交
∠1 和∠2
∠2 和∠3
∠1 和∠3
位置关系
大小关系
1、你能根据这几对角的位置关系,对它们进行分类吗?
∠3 和∠4
∠4 和∠1
∠2 和∠4
2、观察∠1和∠2的顶点和两边,有怎样的位置关系?
1
2
3
4
B
C
D
o
A
分类
邻补角
两直线相交
位置关系
大小关系
3、类比∠1和∠2,看∠1和∠3有怎样的位置关系?
∠1 和∠2
∠2 和∠
∠1 和∠3
3
∠3 和∠4
∠4 和∠1
∠2 和∠4
1
3
B
C
D
A
o
分类
邻补角
两直线相交
对顶角
位置关系
大小关系
4、你能写出邻补角∠1和∠2的大小关系式吗?
∠1+∠2=180°
∠2+∠3=180°
∠3+∠4=180°
∠4+∠1=180°
∠1 和∠2
∠2 和∠
∠1 和∠3
3
∠3 和∠4
∠4 和∠1
∠2 和∠4
探究点二:对顶角、邻补角的性质
分类
邻补角
两直线相交
对顶角
位置关系
大小关系
∠1+∠2=180°
∠2+∠3=180°
∠3+∠4=180°
∠4+∠1=180°
5、你能得到对顶角∠1和∠3的大小关系吗?
∠1 和∠2
∠2 和∠
∠1 和∠3
3
∠3 和∠4
∠4 和∠1
∠2 和∠4
∠ 2 +∠3= ,
4、你能得到对顶角∠1和∠3的大小关系吗?
∠2与∠3互补
∠1与∠2互补,
那么∠ 2 +∠1= ,
∠1= ∠3
180°
180°
由同角的补角相等可知
动动脑:为什么?
分类
邻补角
两直线相交
对顶角
位置关系
大小关系
∠1+∠2=180°
∠2+∠3=180°
∠3+∠4=180°
∠4+∠1=180°
邻补角、对顶角的位置关系和大小关系
∠1=∠3
∠2=∠4
∠1 和∠2
∠2 和∠
∠1 和∠3
3
∠3 和∠4
∠4 和∠1
∠2 和∠4
例1、如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数。
a
b
)
(
1
3
4
2
)
(
解:由邻补角的定义可知
∠2=180°-∠1
=180°-40°=140°
由对顶角相等可得
∠3=∠1=40°,∠4=∠2=140°
变式:直线AB、CD相交与点O,∠AOC=40°,OE平分∠AOC,求∠DOE的度数。
解:∵OE平分∠AOC, 且∠AOC =40°
∴∠COE= ∠AOC=20°
∴∠DOE=180°-∠COE=120°
判断题:
1.如果两个角有公共顶点和一条公共边,而且这两角互为补角, 那么它们互为邻补角.
( × )
2.两条直线相交,如果它们所成的邻补角相等,那么一对对顶角就互补.
( √ )
课堂练习
填空题:
3.如图 ,直线AB、CD、EF相交于点O,∠BOE的对顶角是_______,∠COF 的邻补角是_____________
若∠AOC:∠AOE=2:3,∠EOD=130°,则∠BOC=__________
4.如图 ,直线AB、CD相交于点O,∠COE=90°,∠AOC=30°,∠FOB=90°, 则∠EOF=_____.
∠COF
∠COE和DOF
160°
150°
对顶角和邻补角各有什么特征?产生这两
类角的前提是什么?
2.对顶角有什么性质?这个性质是怎么推导
出来的?
3.两条直线相交形成的四个角中,有几对对
顶角?几对邻补角?
课堂小结
