2.1.2离散型随机变量的分布列(共36张PPT)
文档属性
| 名称 | 2.1.2离散型随机变量的分布列(共36张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-23 10:30:42 | ||
图片预览











文档简介
(共36张PPT)
2.1.2离散型随机变量的分布列
断案——兔子是谁打死的?
在还未禁猎的年代,有一天,两位猎人同时发射一枪,打死一只正在奔驰的野兔,二人直奔猎物,都想得到这个战利品,于是争论起来.
一智者路过此地,问明事由,出面调解,猎人甲称:“我的枪法百发百中,兔子是我打死的.”猎人乙争辩道:“我的枪法比他准,兔子分明是我打中的.”智者道:“你们不必争吵了,听我安排. ”智者命二人向同一目标各打五枪,甲的命中率为0.4,乙的命中率为0.6 . 甲以为这下完了,兔子必判给乙,很丧气,扭头便走,智者喊到:“且慢,听我慢慢道来.”
智者经计算,告诉二人:“既然兔子已被你们打死,那么甲单独击中的机会是0.4,乙单独击中的机会是 0.6,二人共同击中的机会是0.24 .”他建议:“如果此猎物价值若干,你们可按七比十二分配.”结果兔子卖了五十七元,甲分得二十一元,乙分得三十六元,两人皆大欢喜,欣然而归.
请同学们想一想,这个分配方案是否合理?智者是如何做出这个分配方案的?
抛掷一枚骰子,求所得点数及取各值的概率.
X 1 2 3 4 5 6
P
1.分布列
设离散型随机变量ξ可能取得值为
x1,x2,x3,…,
ξ取每一个值xi(i=1,2,…)的概率为
P(ξ= xi)=pi,则称表
为随机变量ξ的概率分布,简称ξ的分布列.
ξ x1 x2 … xi …
P P1 P2 … Pi …
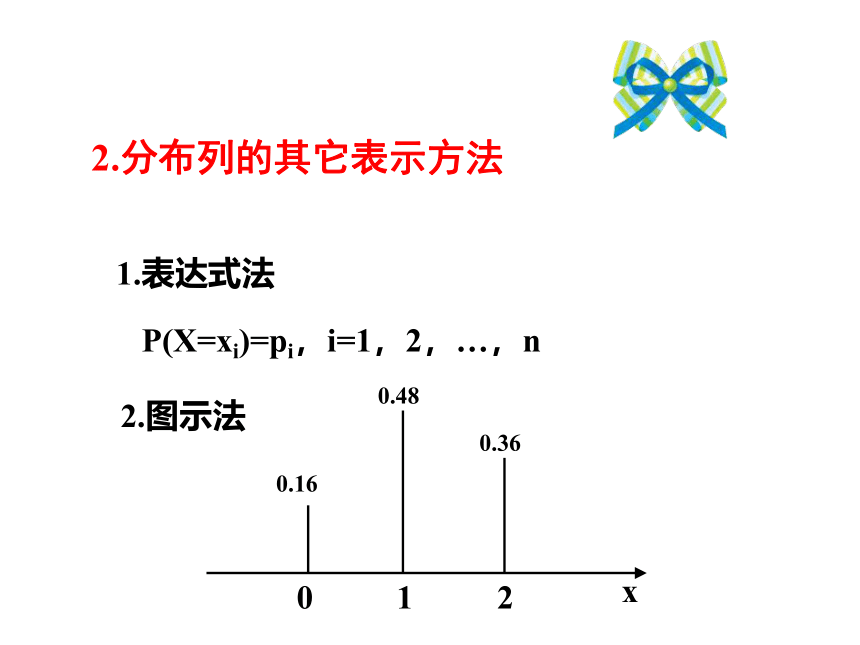
2.分布列的其它表示方法
1.表达式法
P(X=xi)=pi,i=1,2,…,n
2.图示法
离散型随机变量的分布列有何性质?
函数可以用解析式,表格或图象表示,离散性随即变量的分布列也可以用解析式,表格或图象表示.
2.离散型随机变量的分布列的性质
任何随机事件发生的概率都满足:0≤Pi≤1,并且不可能事件的概率为0,必然事件的概率为1.由此你可以得出离散型随机变量的分布列都具有下面两个性质:
⑴Pi≥0,i=1,2,…;
⑵P1+P2+…=1.
3.两点分布
只有两个可能取值的随机变量所服从的分布,称为两点分布. 其概率函数为
P{ξ=xk}=pk (k=0,1)
X 0 1
P 1-p p
一批产品的废品率为5%,从中任意抽取一个进行检验,用随机变量来描述废品出现的情况.即写出分布列.
解?:
这个试验中,用ξ表示废品的个数,显然ξ只可能取0及1两个值.
ξ=0,表示“产品是废品”,即P(ξ=0)=1-5%=95%
ξ=1,表示“产品为合格品”,其概率为这批产品的合格率,即??P(ξ=1)=5%?,
列成概率分布表如下所示:
ξ 0 1
P 95% 5%
两点分布又称0-1分布.由于只有两个可能结果的随机试验叫伯努利试验,所以还称这种分布为伯努利分布.
两点分布列的应用非常广泛.例如抽取的彩票是否中奖,买回的一件产品是否为正品,新生婴儿的性别,投篮是否命中等,都可以用两点分布列来研究.
在含有5件次品的100件产品中,任取3件,求:
(1)取到的次品数X的分布列;
(2)至少取到一件次品的概率.
解:
(1)因为从100件产品中任取3件的结果数为C1003,从100件产品中任取3件,其中恰有k件次品的结果数为C5kC953-k,所以100件产品中任取3件,其中恰有k件次品的概率为
P(X=k)= C5kC953-k / C1003 ,k=0,1,2,3 .
因此随机变量的分布列为
(2)根据随机变量X的分布列,可得至少取到1件次品的概率为
P(X>=1)=P(X=1)+P(X=2)+P(X=3)
≈0.13806+0.00588+0.00006
=0.14400
X 0 1 2 3
P
4.超几何分布
一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则
P(X=k)= CMkCN-Mn-k / CNn ,k=0,1,2,…,m, 即
其中m=min{M,n},且n<=N,M<=N,n,M,N N*.
如果随机变量X的分布列具有上表形式,则称随机变量X服从超几何分布.
X 0 1 … m
P …
某一射手射击所得的环数ξ的分布列如下:
求此射手“射击一次命中环数≥7”的概率.
ξ 4 5 6 7 8 9 10
P 0.02 0.04 0.06 0.09 0.28 0.29 0.22
分析:“射击一次命中环数≥7”是指互斥事件“ξ=7”、“ξ=8”、“ξ=9”、“ξ=10”的和,根据互斥事件的概率加法公式,可以求得此射手“射击一次命中环数≥7”的概率.
解:根据射手射击所得的环数ξ的分布列,有
P(ξ=7)=0.09,P(ξ=8)=0.28,
P(ξ=9)=0.29,P(ξ=10)=0.22.
所求的概率为 P(ξ≥7)=0.09+0.28+0.29+0.22
=0.88 .
1.离散型随机变量的分布列概念
根据随机变量的概率分布(分布列),可以求随机事件的概率.
2.分布列的三种表示方法
(1)表达式法;
(2)图示法;
(3)表格法.
3.分布列的两条性质
(1)Pi≥0,i=1,2,…;
(2)P1+P2+…=1.
4.两种典型分布
(1)两点分布;
(2)超几何分布.
1.(2018年北京卷理)甲、乙等五名奥运志愿者被随机地分到四个不同的岗位服务,每个岗位至少有一名志愿者.
(Ⅰ)求甲、乙两人同时参加 岗位服务的概率;
(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;
(Ⅲ)设随机变量 为这五名志愿者中参加 岗位服务的人数,求 的分布列.
(Ⅱ)记甲、乙两人同时参加同一岗位服务为事件E, 那么
所以,甲、乙两人不在同一岗位服务的概率是
解:
(Ⅰ)记甲、乙两人同时参加 岗位服务为事件 ,那么 ,
即甲、乙两人同时参加 岗位服务的概率是 .
(Ⅲ)随机变量 可能取的值为1,2.事件“ξ=2”是指有两人同时参加 岗位服务,
则 .
所以 ,ξ的分布列是
ξ 1 2
P 0.75 0.25
1.填空
(1)某批数量较大的商品的次品率为10%,从中任意地连续取出5件,其中次品数ξ的分布列为________.
ξ 0 1 2 3 4 5
P 0.95 0.5×0.94 0.1×0.93 0.01×0.92 4.5×0.14 0.15
(2) 下列给出的是不是某个随机变量的分布列?
①
②
③
④
解:
(1)是.
(2) ,所以它不是随机变量的分布列.
(3) ,所以它不是随机变量的分布列.
2.选择
(1)3设随机变量 的分布列为 ,则a的值为( )
A .1; B.9/13; C.11/13; D.27/13
(2)下列表中能成为随机变量ξ的分布列的是()
√
A.
ξ -1 0 1
P 0.3 0.4 0.4
B.
C.
D.
√
ξ 1 2 3
P 0.4 0.7 -0.1
ξ -1 0 1
P 0.3 0.4 0.3
ξ 1 2 3
P 0.3 0.4 0.4
3.解答题
(1)某厂生产电子元件,其产品的次品率为5%,现从一批产品中的任意连续取出2件,求次品数的概率分布.
解: ξ的取值分别为0、1、2
ξ =0表示抽取两件均为正品 ;
∴p(ξ=0)=C20(1-0.05)2=0.9025 .
ξ =1表示抽取一件正品一件次品;
P(ξ=1)= C21 (1-0.05)×0.05=0.95
ξ =2抽取两件均为次品;
P(ξ=2)= C22 0.052=0.0025
∴ξ的概率分布为:
ξ 0 1 2
p 0.9025 0.095 0.0025
(2)随机变量ξ的分布列为
解:由离散型随机变量的分布列的性质有
解得:
(舍)或
(3)设随机变量 的分布列为: ,
求 ① ;
② ;
③ .
解:
① ;
②
③
2.1.2离散型随机变量的分布列
断案——兔子是谁打死的?
在还未禁猎的年代,有一天,两位猎人同时发射一枪,打死一只正在奔驰的野兔,二人直奔猎物,都想得到这个战利品,于是争论起来.
一智者路过此地,问明事由,出面调解,猎人甲称:“我的枪法百发百中,兔子是我打死的.”猎人乙争辩道:“我的枪法比他准,兔子分明是我打中的.”智者道:“你们不必争吵了,听我安排. ”智者命二人向同一目标各打五枪,甲的命中率为0.4,乙的命中率为0.6 . 甲以为这下完了,兔子必判给乙,很丧气,扭头便走,智者喊到:“且慢,听我慢慢道来.”
智者经计算,告诉二人:“既然兔子已被你们打死,那么甲单独击中的机会是0.4,乙单独击中的机会是 0.6,二人共同击中的机会是0.24 .”他建议:“如果此猎物价值若干,你们可按七比十二分配.”结果兔子卖了五十七元,甲分得二十一元,乙分得三十六元,两人皆大欢喜,欣然而归.
请同学们想一想,这个分配方案是否合理?智者是如何做出这个分配方案的?
抛掷一枚骰子,求所得点数及取各值的概率.
X 1 2 3 4 5 6
P
1.分布列
设离散型随机变量ξ可能取得值为
x1,x2,x3,…,
ξ取每一个值xi(i=1,2,…)的概率为
P(ξ= xi)=pi,则称表
为随机变量ξ的概率分布,简称ξ的分布列.
ξ x1 x2 … xi …
P P1 P2 … Pi …
2.分布列的其它表示方法
1.表达式法
P(X=xi)=pi,i=1,2,…,n
2.图示法
离散型随机变量的分布列有何性质?
函数可以用解析式,表格或图象表示,离散性随即变量的分布列也可以用解析式,表格或图象表示.
2.离散型随机变量的分布列的性质
任何随机事件发生的概率都满足:0≤Pi≤1,并且不可能事件的概率为0,必然事件的概率为1.由此你可以得出离散型随机变量的分布列都具有下面两个性质:
⑴Pi≥0,i=1,2,…;
⑵P1+P2+…=1.
3.两点分布
只有两个可能取值的随机变量所服从的分布,称为两点分布. 其概率函数为
P{ξ=xk}=pk (k=0,1)
X 0 1
P 1-p p
一批产品的废品率为5%,从中任意抽取一个进行检验,用随机变量来描述废品出现的情况.即写出分布列.
解?:
这个试验中,用ξ表示废品的个数,显然ξ只可能取0及1两个值.
ξ=0,表示“产品是废品”,即P(ξ=0)=1-5%=95%
ξ=1,表示“产品为合格品”,其概率为这批产品的合格率,即??P(ξ=1)=5%?,
列成概率分布表如下所示:
ξ 0 1
P 95% 5%
两点分布又称0-1分布.由于只有两个可能结果的随机试验叫伯努利试验,所以还称这种分布为伯努利分布.
两点分布列的应用非常广泛.例如抽取的彩票是否中奖,买回的一件产品是否为正品,新生婴儿的性别,投篮是否命中等,都可以用两点分布列来研究.
在含有5件次品的100件产品中,任取3件,求:
(1)取到的次品数X的分布列;
(2)至少取到一件次品的概率.
解:
(1)因为从100件产品中任取3件的结果数为C1003,从100件产品中任取3件,其中恰有k件次品的结果数为C5kC953-k,所以100件产品中任取3件,其中恰有k件次品的概率为
P(X=k)= C5kC953-k / C1003 ,k=0,1,2,3 .
因此随机变量的分布列为
(2)根据随机变量X的分布列,可得至少取到1件次品的概率为
P(X>=1)=P(X=1)+P(X=2)+P(X=3)
≈0.13806+0.00588+0.00006
=0.14400
X 0 1 2 3
P
4.超几何分布
一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则
P(X=k)= CMkCN-Mn-k / CNn ,k=0,1,2,…,m, 即
其中m=min{M,n},且n<=N,M<=N,n,M,N N*.
如果随机变量X的分布列具有上表形式,则称随机变量X服从超几何分布.
X 0 1 … m
P …
某一射手射击所得的环数ξ的分布列如下:
求此射手“射击一次命中环数≥7”的概率.
ξ 4 5 6 7 8 9 10
P 0.02 0.04 0.06 0.09 0.28 0.29 0.22
分析:“射击一次命中环数≥7”是指互斥事件“ξ=7”、“ξ=8”、“ξ=9”、“ξ=10”的和,根据互斥事件的概率加法公式,可以求得此射手“射击一次命中环数≥7”的概率.
解:根据射手射击所得的环数ξ的分布列,有
P(ξ=7)=0.09,P(ξ=8)=0.28,
P(ξ=9)=0.29,P(ξ=10)=0.22.
所求的概率为 P(ξ≥7)=0.09+0.28+0.29+0.22
=0.88 .
1.离散型随机变量的分布列概念
根据随机变量的概率分布(分布列),可以求随机事件的概率.
2.分布列的三种表示方法
(1)表达式法;
(2)图示法;
(3)表格法.
3.分布列的两条性质
(1)Pi≥0,i=1,2,…;
(2)P1+P2+…=1.
4.两种典型分布
(1)两点分布;
(2)超几何分布.
1.(2018年北京卷理)甲、乙等五名奥运志愿者被随机地分到四个不同的岗位服务,每个岗位至少有一名志愿者.
(Ⅰ)求甲、乙两人同时参加 岗位服务的概率;
(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;
(Ⅲ)设随机变量 为这五名志愿者中参加 岗位服务的人数,求 的分布列.
(Ⅱ)记甲、乙两人同时参加同一岗位服务为事件E, 那么
所以,甲、乙两人不在同一岗位服务的概率是
解:
(Ⅰ)记甲、乙两人同时参加 岗位服务为事件 ,那么 ,
即甲、乙两人同时参加 岗位服务的概率是 .
(Ⅲ)随机变量 可能取的值为1,2.事件“ξ=2”是指有两人同时参加 岗位服务,
则 .
所以 ,ξ的分布列是
ξ 1 2
P 0.75 0.25
1.填空
(1)某批数量较大的商品的次品率为10%,从中任意地连续取出5件,其中次品数ξ的分布列为________.
ξ 0 1 2 3 4 5
P 0.95 0.5×0.94 0.1×0.93 0.01×0.92 4.5×0.14 0.15
(2) 下列给出的是不是某个随机变量的分布列?
①
②
③
④
解:
(1)是.
(2) ,所以它不是随机变量的分布列.
(3) ,所以它不是随机变量的分布列.
2.选择
(1)3设随机变量 的分布列为 ,则a的值为( )
A .1; B.9/13; C.11/13; D.27/13
(2)下列表中能成为随机变量ξ的分布列的是()
√
A.
ξ -1 0 1
P 0.3 0.4 0.4
B.
C.
D.
√
ξ 1 2 3
P 0.4 0.7 -0.1
ξ -1 0 1
P 0.3 0.4 0.3
ξ 1 2 3
P 0.3 0.4 0.4
3.解答题
(1)某厂生产电子元件,其产品的次品率为5%,现从一批产品中的任意连续取出2件,求次品数的概率分布.
解: ξ的取值分别为0、1、2
ξ =0表示抽取两件均为正品 ;
∴p(ξ=0)=C20(1-0.05)2=0.9025 .
ξ =1表示抽取一件正品一件次品;
P(ξ=1)= C21 (1-0.05)×0.05=0.95
ξ =2抽取两件均为次品;
P(ξ=2)= C22 0.052=0.0025
∴ξ的概率分布为:
ξ 0 1 2
p 0.9025 0.095 0.0025
(2)随机变量ξ的分布列为
解:由离散型随机变量的分布列的性质有
解得:
(舍)或
(3)设随机变量 的分布列为: ,
求 ① ;
② ;
③ .
解:
① ;
②
③
