2.4正态分布(共36张PPT)
图片预览









文档简介
(共36张PPT)
2.4 正态分布
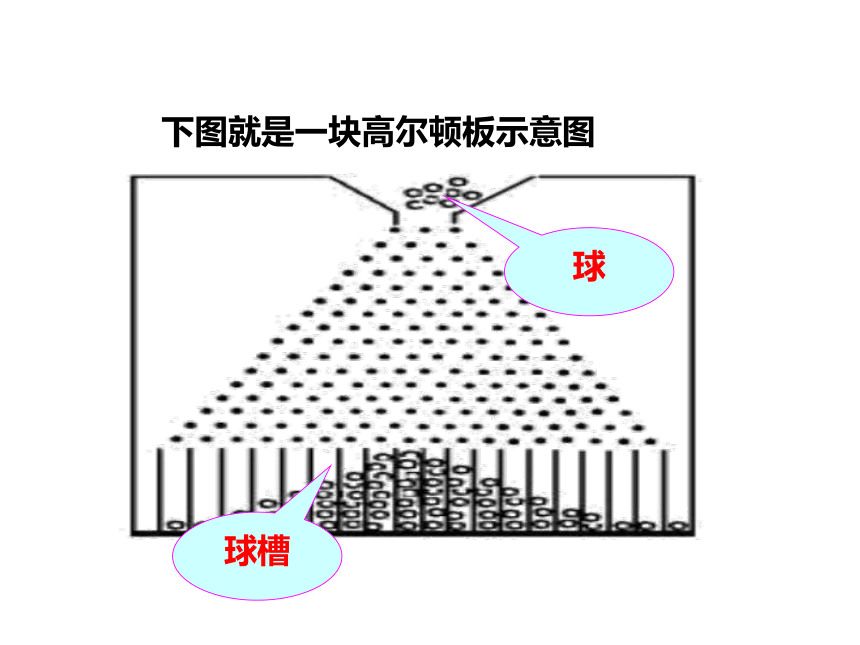
在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,最后掉入高尔顿板下方的某一球槽内.
你见过高尔顿板吗?
下图就是一块高尔顿板示意图
球槽
球
如果把球槽编号,就可以考察球到底是落在第几号球槽中.重复进行高尔顿板试验,随着试验次数的增加,掉入各个球槽内的小球的个数就会越来越多,堆积的高度也会越来越高.各个球槽内的堆积高度反映了小球掉入各球槽的个数多少.
这节课我们就学习——正态分布
请根据高尔顿板的模型画出频率分布直方图.
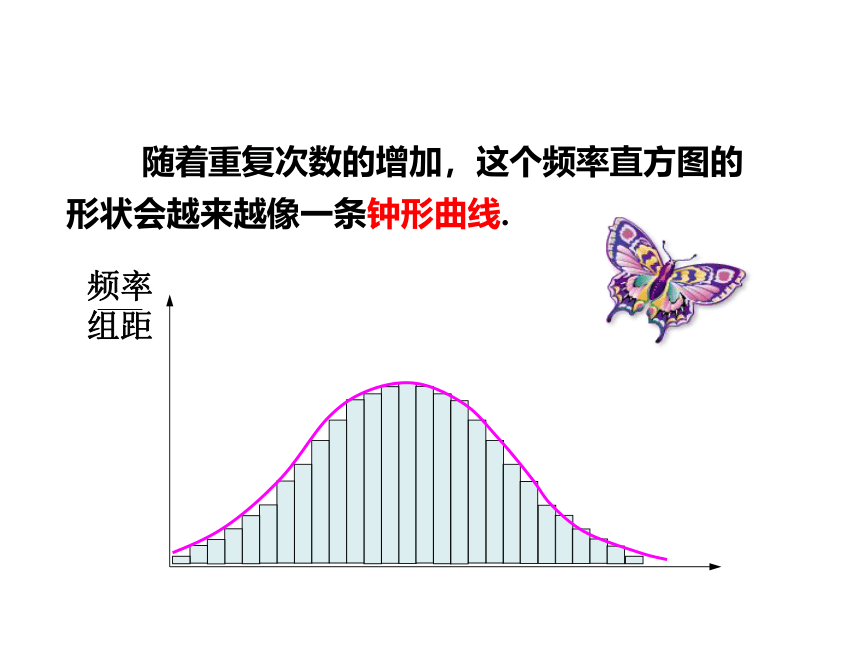
随着重复次数的增加,这个频率直方图的形状会越来越像一条钟形曲线.
1.正态曲线
上图曲线(或近似地是)下面函数的图像
其中实数μ和?(? >0)为参数.我们称f(x)的图像为正态分布密度曲线,简称正态曲线.
如果去掉高尔顿板试验中最下边的球槽,并沿着其底部建立一个水平坐标轴,其刻度单位为球槽的宽度,用X表示落下的小球第1次与高尔顿板底部接触时的坐标,则X是一个随机变量. X落在区间(a,b]的概率为
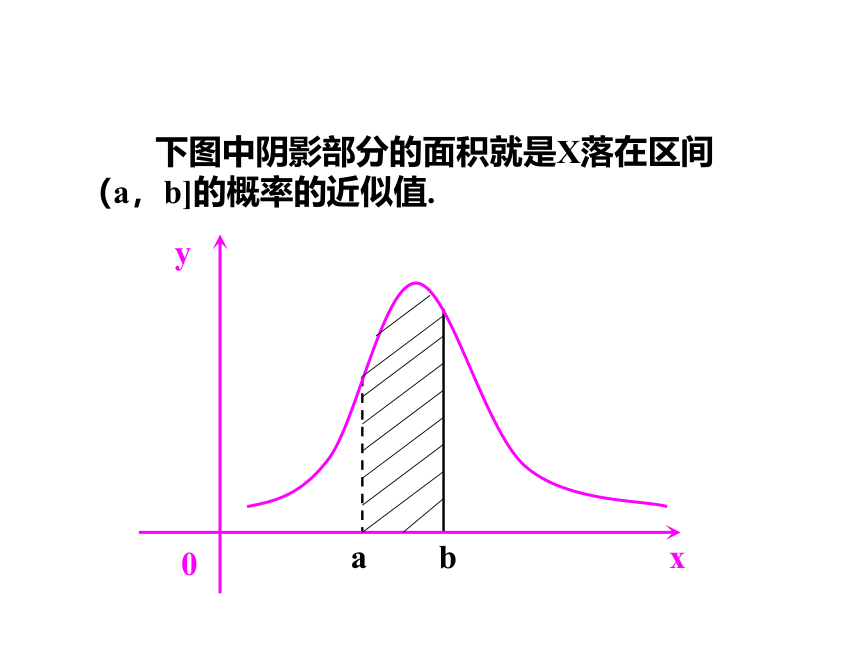
即由正态曲线,过点(a,0)和(b,0)的两条x轴的垂线,及x轴所围成的平面图形的面积,就是X落在区间(a,b]的概率的近似值.
下图中阴影部分的面积就是X落在区间(a,b]的概率的近似值.
2.正态分布
一般地,如果对于任何实数a,b(a 则称随机变量X服从正态分布(normal distribution).正态分布完全由参数μ和? 确定,因此正态分布常记作N(μ,?2).如果随机变量X服从正态分布,则记为X~N(μ,?2).
经验表明,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,他就服从或近似服从正态分布.
早在1733年,法国数学家棣莫弗就用n!的近似公式得到了正态分布.之后,德国数学家高斯在研究测量误差时从另一个角度导出了它,并研究了它的性质,因此,人们也称正态分布为高斯分布.
在现实生活中,很多随机变量都服从或近似服从正态分布.例如:
(1)长度测量的误差;
(2)某一地区同年龄人群的身高、体重、肺活量;
(3)一定条件下生长的小麦的株高、穗长、
单位面积产量;
(4)正常生长条件下各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命).
(1)曲线位于x轴上方,与x轴不相交;
(2)曲线是单峰的,它关于直线x=μ对称;
(3)曲线在x=μ处达到峰值 ;
(4)曲线与x轴之间的面积为1.
你能说说正态曲线的特点吗?
(5) 当? 一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移.
当μ一定时,曲线的形状由? 确定, ? 越小,曲线越“瘦高”,表示总体的分布越集中; ? 越大,曲线越“矮胖”,表示总体的分布越分散.
若X~ N(μ,? 2),则对于任何实数a>0,
为右图中阴影部分的面积,对于固定的μ和a而言,该面积随着? 的减少而变大.这说明? 越小,X落在区间(μ-a, μ+a]的概率越大,即X集中在μ周围概率越大.
特别有
P(μ- ?P(μ- 2?P(μ- 3? 上述结果用右图表示
由图可知,正态分布几乎总取之于区间(μ- 3?,μ+3? )之间.而在此区间之外取值的概率只有0.0026,通常认为这种情况在一次试验中几乎不可能发生.
在实际应用中,通常认为服从于正态分布N(μ,?2 )的随机变量X只取(μ- 3?,μ+3? )之间的值,并简称之为3?原则.
1. 正态总体函数解析式
2. 正态曲线
3. 正态曲线的性质
(1)曲线在x轴的上方,与x轴不相交;
(2)曲线关于直线x=μ对称;
(3)曲线在x=μ时位于最高点;
(4)当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以轴为渐近线,向它无限靠近;
(5)当μ一定时,曲线的形状由σ确定.σ越大,曲线越“矮胖”,表示总体的分布越分散;σ越小,曲线越“瘦高”,表示总体的分布越集中.
4.标准正态分布
(2)“标准正态分布表”
1.(2018年安徽)设两个正态分布N(μ1,?12) (?1>0)和N(μ2,?22)(?2>0)的密度函数图像如图所示,则有( )
A. μ1<μ2, ?1< ?2 B. μ1<μ2, ?1>?2
C. μ1>μ2, ?1< ?2 D. μ1>μ2, ?1> ?2
A
解析:由正态分布性质知,x=μ为正态密度函数图像的对称轴,故μ1<μ2,又? 越小,图像越瘦高,故?1 2. (2018年湖南)设随机变量X服从正态分布N(2,9),若P(X>c+1)=P(X A.1 B.2 C.3 D.4
解析:
∵ξ~N(2,9),
∴P(ξ>c+1)=P(ξ<3-c).
又P(ξ>c+1)=P(ξ ∴3 –c=c-1, ∴c=2.
B
3.(2017年重庆理)已知随机变量ξ服从正态分布N(3,? 2),则P(ξ<3)等于( )
A.1/5 B.1/4 C.1/3 D.1/2
解析:由正态分布图像知,μ=3为该图像的对称轴,P(ξ<3)=P(ξ>3)=1/2.
D
1.填空
给出下列三个正态总体的函数表达式,请找出其均值μ和标准差σ
答案:(1)0,1;(2)1,2;(3)-1,0.5
(1)
(3)
(2)
(1)若随机变量ξ~ N(μ,σ2),且Dξ=1,Eξ=3,则P(-1<ξ≤1)等于( )
A. 2Φ(1)-1 B. Φ(4)-Φ(2)
C. Φ(-4)-Φ(-2) D. Φ(2)-Φ(4)
(2)在正态总体N(0,)中,数值落在(-∞, -1)∪(1,+∞)里的概率为( )
A. 0.097 B. 0.046
C. 0.03 D. 0.003
2.选择
√
√
3.解答题
(1)求标准正态总体在(-1,2)内取值的概率.
解:利用等式 有
①从该车间工人中任选一人,其完成该道工序的时间不到7分钟的概率;
②为了保证生产连续进行,要求以95%的概率保证该道工序上工人完成工作时间不多于15分钟,这一要求能否得到保证?
解 :
即该道工序可以95%的概率保证工人完成工作的时间不多于15分钟,因此生产可连续进行.
解:
(4)出生体重低于2500克为低体重儿.若由某项研究得某地婴儿出生体重均数为3200克,标准差为350克,估计该地当年低体重儿所占的比例.
解:
记x为当年该地婴儿出生体重,则x服从正态分布N(3200,3502)
P(x<2500)
查标准正态分布界值表 Φ(-2)=0.0228
即估计该地当年低体重儿所占的比例为2.28% .
(5)估计某单位101名正常成年女子血清总胆固醇的参考值范围.假设该资料服从正态分布.
已知:
计算95%的参考范围(双侧)
结论:正常成年女子血清总胆固醇95%的参考值范围为2.78-5.34(mmol/l).
解:
2.4 正态分布
在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块,小木块之间留有适当的空隙作为通道,前面挡有一块玻璃.让一个小球从高尔顿板上方的通道口落下,小球在下落的过程中与层层小木块碰撞,最后掉入高尔顿板下方的某一球槽内.
你见过高尔顿板吗?
下图就是一块高尔顿板示意图
球槽
球
如果把球槽编号,就可以考察球到底是落在第几号球槽中.重复进行高尔顿板试验,随着试验次数的增加,掉入各个球槽内的小球的个数就会越来越多,堆积的高度也会越来越高.各个球槽内的堆积高度反映了小球掉入各球槽的个数多少.
这节课我们就学习——正态分布
请根据高尔顿板的模型画出频率分布直方图.
随着重复次数的增加,这个频率直方图的形状会越来越像一条钟形曲线.
1.正态曲线
上图曲线(或近似地是)下面函数的图像
其中实数μ和?(? >0)为参数.我们称f(x)的图像为正态分布密度曲线,简称正态曲线.
如果去掉高尔顿板试验中最下边的球槽,并沿着其底部建立一个水平坐标轴,其刻度单位为球槽的宽度,用X表示落下的小球第1次与高尔顿板底部接触时的坐标,则X是一个随机变量. X落在区间(a,b]的概率为
即由正态曲线,过点(a,0)和(b,0)的两条x轴的垂线,及x轴所围成的平面图形的面积,就是X落在区间(a,b]的概率的近似值.
下图中阴影部分的面积就是X落在区间(a,b]的概率的近似值.
2.正态分布
一般地,如果对于任何实数a,b(a
经验表明,一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,他就服从或近似服从正态分布.
早在1733年,法国数学家棣莫弗就用n!的近似公式得到了正态分布.之后,德国数学家高斯在研究测量误差时从另一个角度导出了它,并研究了它的性质,因此,人们也称正态分布为高斯分布.
在现实生活中,很多随机变量都服从或近似服从正态分布.例如:
(1)长度测量的误差;
(2)某一地区同年龄人群的身高、体重、肺活量;
(3)一定条件下生长的小麦的株高、穗长、
单位面积产量;
(4)正常生长条件下各种产品的质量指标(如零件的尺寸、纤维的纤度、电容器的电容量、电子管的使用寿命).
(1)曲线位于x轴上方,与x轴不相交;
(2)曲线是单峰的,它关于直线x=μ对称;
(3)曲线在x=μ处达到峰值 ;
(4)曲线与x轴之间的面积为1.
你能说说正态曲线的特点吗?
(5) 当? 一定时,曲线的位置由μ确定,曲线随着μ的变化而沿x轴平移.
当μ一定时,曲线的形状由? 确定, ? 越小,曲线越“瘦高”,表示总体的分布越集中; ? 越大,曲线越“矮胖”,表示总体的分布越分散.
若X~ N(μ,? 2),则对于任何实数a>0,
为右图中阴影部分的面积,对于固定的μ和a而言,该面积随着? 的减少而变大.这说明? 越小,X落在区间(μ-a, μ+a]的概率越大,即X集中在μ周围概率越大.
特别有
P(μ- ?
由图可知,正态分布几乎总取之于区间(μ- 3?,μ+3? )之间.而在此区间之外取值的概率只有0.0026,通常认为这种情况在一次试验中几乎不可能发生.
在实际应用中,通常认为服从于正态分布N(μ,?2 )的随机变量X只取(μ- 3?,μ+3? )之间的值,并简称之为3?原则.
1. 正态总体函数解析式
2. 正态曲线
3. 正态曲线的性质
(1)曲线在x轴的上方,与x轴不相交;
(2)曲线关于直线x=μ对称;
(3)曲线在x=μ时位于最高点;
(4)当 x<μ时,曲线上升;当x>μ时,曲线下降.并且当曲线向左、右两边无限延伸时,以轴为渐近线,向它无限靠近;
(5)当μ一定时,曲线的形状由σ确定.σ越大,曲线越“矮胖”,表示总体的分布越分散;σ越小,曲线越“瘦高”,表示总体的分布越集中.
4.标准正态分布
(2)“标准正态分布表”
1.(2018年安徽)设两个正态分布N(μ1,?12) (?1>0)和N(μ2,?22)(?2>0)的密度函数图像如图所示,则有( )
A. μ1<μ2, ?1< ?2 B. μ1<μ2, ?1>?2
C. μ1>μ2, ?1< ?2 D. μ1>μ2, ?1> ?2
A
解析:由正态分布性质知,x=μ为正态密度函数图像的对称轴,故μ1<μ2,又? 越小,图像越瘦高,故?1 2. (2018年湖南)设随机变量X服从正态分布N(2,9),若P(X>c+1)=P(X
解析:
∵ξ~N(2,9),
∴P(ξ>c+1)=P(ξ<3-c).
又P(ξ>c+1)=P(ξ
B
3.(2017年重庆理)已知随机变量ξ服从正态分布N(3,? 2),则P(ξ<3)等于( )
A.1/5 B.1/4 C.1/3 D.1/2
解析:由正态分布图像知,μ=3为该图像的对称轴,P(ξ<3)=P(ξ>3)=1/2.
D
1.填空
给出下列三个正态总体的函数表达式,请找出其均值μ和标准差σ
答案:(1)0,1;(2)1,2;(3)-1,0.5
(1)
(3)
(2)
(1)若随机变量ξ~ N(μ,σ2),且Dξ=1,Eξ=3,则P(-1<ξ≤1)等于( )
A. 2Φ(1)-1 B. Φ(4)-Φ(2)
C. Φ(-4)-Φ(-2) D. Φ(2)-Φ(4)
(2)在正态总体N(0,)中,数值落在(-∞, -1)∪(1,+∞)里的概率为( )
A. 0.097 B. 0.046
C. 0.03 D. 0.003
2.选择
√
√
3.解答题
(1)求标准正态总体在(-1,2)内取值的概率.
解:利用等式 有
①从该车间工人中任选一人,其完成该道工序的时间不到7分钟的概率;
②为了保证生产连续进行,要求以95%的概率保证该道工序上工人完成工作时间不多于15分钟,这一要求能否得到保证?
解 :
即该道工序可以95%的概率保证工人完成工作的时间不多于15分钟,因此生产可连续进行.
解:
(4)出生体重低于2500克为低体重儿.若由某项研究得某地婴儿出生体重均数为3200克,标准差为350克,估计该地当年低体重儿所占的比例.
解:
记x为当年该地婴儿出生体重,则x服从正态分布N(3200,3502)
P(x<2500)
查标准正态分布界值表 Φ(-2)=0.0228
即估计该地当年低体重儿所占的比例为2.28% .
(5)估计某单位101名正常成年女子血清总胆固醇的参考值范围.假设该资料服从正态分布.
已知:
计算95%的参考范围(双侧)
结论:正常成年女子血清总胆固醇95%的参考值范围为2.78-5.34(mmol/l).
解:
