人教版数学三年级下册第八单元数学广角-搭配同步练习(3课时 含解析)
文档属性
| 名称 | 人教版数学三年级下册第八单元数学广角-搭配同步练习(3课时 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-23 19:57:21 | ||
图片预览




文档简介
第1课时搭 配(1)
用2、5、6、0四个数可以组成多少个没有重复数字的两位数?
2.4个小朋友排成一队。队长小美站在最前面,其他人可以任意换位置,一共有多少种排法?
3.把5辆玩具车全部分给小龙、小华和小亮,每人至少分一辆,有多少种分法?
4.按下面的要求,从4、5、O、9中选两个数组成没有重复数字的小数。
(1)小于1的一位小数。
(2)大于5的一位小数。
5.数一数,下图中一共有( )条线段。
第2课时搭 配(2)
1.下图是食堂盒饭的菜品。如果每份盒饭一荤一素搭配,有多少种不同的搭配呢?
学生的副餐有一袋牛奶和一份点心,牛奶有3种不同的口味,点心有5个不同的种类。共有多少种不同的搭配?
用“红、黄、绿”三个字分别与“花、色、豆、衣”四个字组词,共有几种不同的组法?所组的词有哪些?
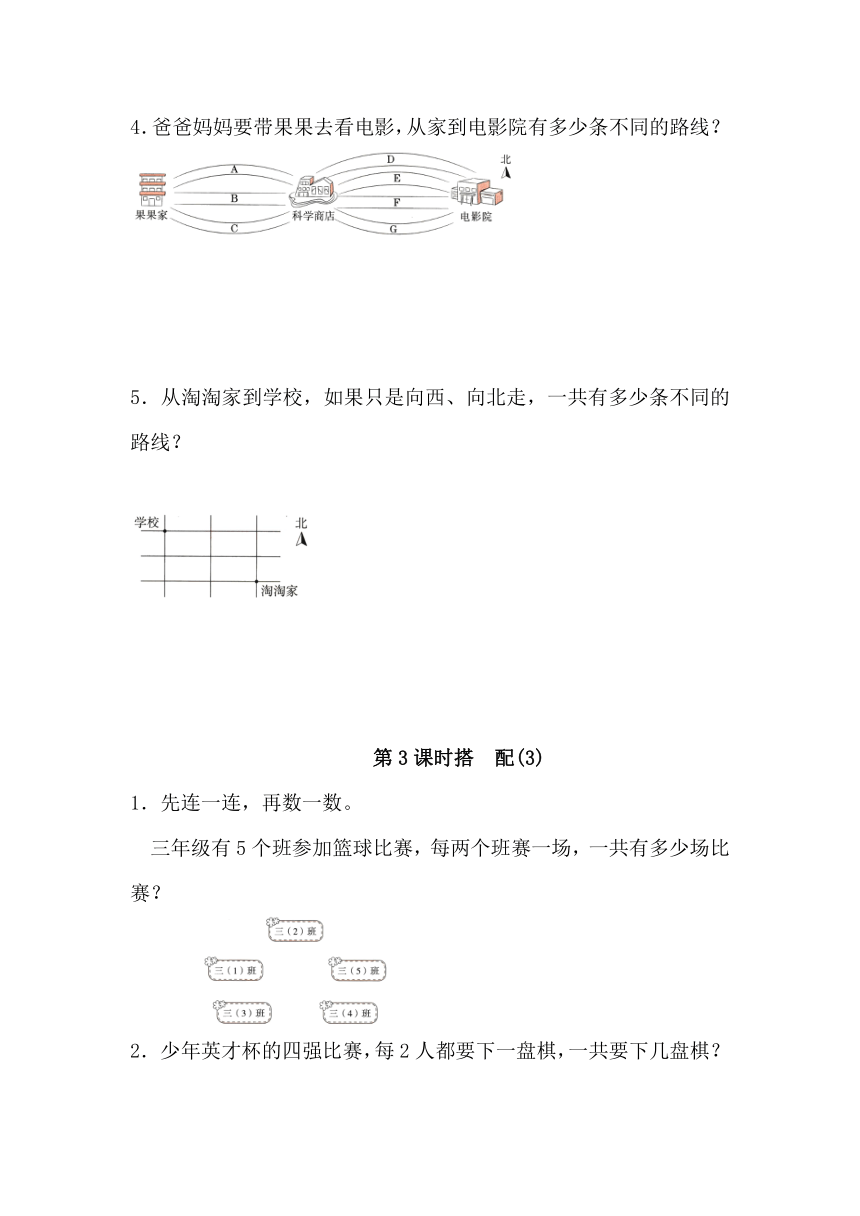
4.爸爸妈妈要带果果去看电影,从家到电影院有多少条不同的路线?
5.从淘淘家到学校,如果只是向西、向北走,一共有多少条不同的路线?
第3课时搭 配(3)
1.先连一连,再数一数。
三年级有5个班参加篮球比赛,每两个班赛一场,一共有多少场比赛?
少年英才杯的四强比赛,每2人都要下一盘棋,一共要下几盘棋?
3.华博机器人学校六一儿童节期间凭宣传单可免费听两节课。
(1)徐新刚想从上面的4种课程里选择2种来听,共有多少种选法?
(2)李涵想选百变工程和另一种课程,共有多少种选法?
4.几个朋友相约去公园划船,想从下面的5艘船中挑选2艘,一共有多少种不同的选法?
5.数一数,下图中一共有( )个长方形。
第1课时 搭配(1)
1.答:用2、5、6、O四个数可以组成9个没有重复数字的两位数。
解析 组成两位数,也就是十位和个位,用固定十位法,可以固定3次,分别是2、5、6。当十位是2时,个位可以是5、6、O,能组成3个两位数;同理当十位是5时,可以组成52、56、50三个数;当十位是6时,也可以组成3个数。所以一共能组成9个没有重复数字的两位数。
2.答:一共有6种排法。
解析 按一定的顺序排列,做到不重复、不遗漏。因为小美要站在最前面,其他的人可以任意换位置,可以先确定第二个人的位置,再确定后两个人的位置。列表如下:
序号 第二个人 第三个人 第四个人
排列1 小明 小芳 小刚
排列2 小明 小刚 小芳
排列3 小芳 小明 小刚
排列4 小芳 小刚 小明
排列5 小刚 小芳 小明
排列6 小刚 小明 小芳
3.答:有6种分法。
解析 可以用列表的方法,按一定规律把玩具车分给三个人。列表如下:
序号 小龙 小华 小亮
分法1 1 1 3
分法2 1 2 2
分法3 1 3 1
分法4 2 1 2
分法5 2 2 1
分法6 3 1 1
4.(1)0.4 0.5 0.9
解析 小于1的一位小数,也就是整数部分是0的小数,把0放在整数部分,小数部分4、5、9任选,所以满足条件的小数有0.4、0.5、0.9。
(2)5.4 5.9 9.O 9.4 9.5
解析 大于5的一位小数,也就是整数部分必须大于或等于5。因为是选两个数组成一位小数,所以整数部分只有个位,大于或等于5的有5、9。整数部分是5,小数部分可以是4、9;整数部分是9,小数部分可以是O、4、5。
5. 10
解析 计算法:4+3+2+1=10(条)
画图法:如图。
第2课时 搭配(2)
1.答:有6种不同的搭配。
解析 方法一:用字母A、B表示两种荤菜,用1、2、3表示三种素菜。用连线的方法表示搭配过程。
方法二:2×3=6(种)。
2.答:共有1 5种不同的搭配。
解析 方法一:用字母A、B、C表示3种不同口味的牛奶,用1、2、3、4、5表示5个种类的点心。用连线的方法表示搭配过程。
方法二:3×5=15(种)。
3.答:共有12种不同的组法。所组的词有:红花、红色、红豆、红衣、黄花、黄色、黄豆、黄衣、绿花、绿色、绿豆、绿衣。
解析 方法一:用连线的方法表示搭配过程。
方法二:3×4=12(种)。
4.3×4=12(条)
答:从家到电影院有12条不同的路线。
解析 方法一:用连线的方法表示搭配过程。
方法二:从果果家到科学商店,如果选路线A,继续从科学商店往电影院走有4条不同的路线;同样的,如果选路线B或C,从科学商店往电影院走仍然有4条不同的路线。一共有3个4,3×4=12(条)。
5.答:一共有6条不同的路线。
解析 将图中的所有线段标上序号(如图),按顺序行走,做到不重复、不遗漏。
从淘淘家到学校的路线有:(1)①→②→⑤→⑩;
(2)①→④→⑦→⑩;(3)①→④→⑨→?;(4)③→⑥→⑨→?;(5)③→⑥→⑦→⑩;(6)③→⑧→?→?。
第3课时 搭配(3)
1.
答:一共有10场比赛。
解析 连线如上图。每两个班都要赛一场,从三(1)班开始数,分别与三(2)、三(3)、三(4)、三(5)班赛一场,共四场;三(2)班分别与三(3)、三(4)、三(5)班赛一场,共三场;三(3)班要与三(4)、三(5)班赛一场,共两场;三(4)班与三(5)班赛一场。相加之后的总和为10场。注意避免重复计算。
2.答:一共要下6盘棋。
解析 用A、B、C、D表示这四个同学,用连线的方式数一数。
3.(1)答:共有6种选法。
解析 只需要从4种课程中选出2种课程,与顺序无关,用连线的方式数一数。
(2)答:共有3种选法。
解析 李涵想选的2种课程中有一种百变工程课已确定,另一种课程只能从余下的3种中选出1种,有3种不同的选法。
4.答:一共有10种不同的选法。
解析 只需要考虑选择哪两艘船,与选择这两艘船的顺序无关,用连线法可以直观地表示出来。
5.9
解析 该图既可以从整体上看做一个大的长方形,也可以从横向上看成是两个长方形拼成的一个大长方形。因此要数清楚究竟有多少个长方形,需要数三层:上层、下层和整体。每层都有3个长方形。这样就可以确定,一共有9个长方形。
用2、5、6、0四个数可以组成多少个没有重复数字的两位数?
2.4个小朋友排成一队。队长小美站在最前面,其他人可以任意换位置,一共有多少种排法?
3.把5辆玩具车全部分给小龙、小华和小亮,每人至少分一辆,有多少种分法?
4.按下面的要求,从4、5、O、9中选两个数组成没有重复数字的小数。
(1)小于1的一位小数。
(2)大于5的一位小数。
5.数一数,下图中一共有( )条线段。
第2课时搭 配(2)
1.下图是食堂盒饭的菜品。如果每份盒饭一荤一素搭配,有多少种不同的搭配呢?
学生的副餐有一袋牛奶和一份点心,牛奶有3种不同的口味,点心有5个不同的种类。共有多少种不同的搭配?
用“红、黄、绿”三个字分别与“花、色、豆、衣”四个字组词,共有几种不同的组法?所组的词有哪些?
4.爸爸妈妈要带果果去看电影,从家到电影院有多少条不同的路线?
5.从淘淘家到学校,如果只是向西、向北走,一共有多少条不同的路线?
第3课时搭 配(3)
1.先连一连,再数一数。
三年级有5个班参加篮球比赛,每两个班赛一场,一共有多少场比赛?
少年英才杯的四强比赛,每2人都要下一盘棋,一共要下几盘棋?
3.华博机器人学校六一儿童节期间凭宣传单可免费听两节课。
(1)徐新刚想从上面的4种课程里选择2种来听,共有多少种选法?
(2)李涵想选百变工程和另一种课程,共有多少种选法?
4.几个朋友相约去公园划船,想从下面的5艘船中挑选2艘,一共有多少种不同的选法?
5.数一数,下图中一共有( )个长方形。
第1课时 搭配(1)
1.答:用2、5、6、O四个数可以组成9个没有重复数字的两位数。
解析 组成两位数,也就是十位和个位,用固定十位法,可以固定3次,分别是2、5、6。当十位是2时,个位可以是5、6、O,能组成3个两位数;同理当十位是5时,可以组成52、56、50三个数;当十位是6时,也可以组成3个数。所以一共能组成9个没有重复数字的两位数。
2.答:一共有6种排法。
解析 按一定的顺序排列,做到不重复、不遗漏。因为小美要站在最前面,其他的人可以任意换位置,可以先确定第二个人的位置,再确定后两个人的位置。列表如下:
序号 第二个人 第三个人 第四个人
排列1 小明 小芳 小刚
排列2 小明 小刚 小芳
排列3 小芳 小明 小刚
排列4 小芳 小刚 小明
排列5 小刚 小芳 小明
排列6 小刚 小明 小芳
3.答:有6种分法。
解析 可以用列表的方法,按一定规律把玩具车分给三个人。列表如下:
序号 小龙 小华 小亮
分法1 1 1 3
分法2 1 2 2
分法3 1 3 1
分法4 2 1 2
分法5 2 2 1
分法6 3 1 1
4.(1)0.4 0.5 0.9
解析 小于1的一位小数,也就是整数部分是0的小数,把0放在整数部分,小数部分4、5、9任选,所以满足条件的小数有0.4、0.5、0.9。
(2)5.4 5.9 9.O 9.4 9.5
解析 大于5的一位小数,也就是整数部分必须大于或等于5。因为是选两个数组成一位小数,所以整数部分只有个位,大于或等于5的有5、9。整数部分是5,小数部分可以是4、9;整数部分是9,小数部分可以是O、4、5。
5. 10
解析 计算法:4+3+2+1=10(条)
画图法:如图。
第2课时 搭配(2)
1.答:有6种不同的搭配。
解析 方法一:用字母A、B表示两种荤菜,用1、2、3表示三种素菜。用连线的方法表示搭配过程。
方法二:2×3=6(种)。
2.答:共有1 5种不同的搭配。
解析 方法一:用字母A、B、C表示3种不同口味的牛奶,用1、2、3、4、5表示5个种类的点心。用连线的方法表示搭配过程。
方法二:3×5=15(种)。
3.答:共有12种不同的组法。所组的词有:红花、红色、红豆、红衣、黄花、黄色、黄豆、黄衣、绿花、绿色、绿豆、绿衣。
解析 方法一:用连线的方法表示搭配过程。
方法二:3×4=12(种)。
4.3×4=12(条)
答:从家到电影院有12条不同的路线。
解析 方法一:用连线的方法表示搭配过程。
方法二:从果果家到科学商店,如果选路线A,继续从科学商店往电影院走有4条不同的路线;同样的,如果选路线B或C,从科学商店往电影院走仍然有4条不同的路线。一共有3个4,3×4=12(条)。
5.答:一共有6条不同的路线。
解析 将图中的所有线段标上序号(如图),按顺序行走,做到不重复、不遗漏。
从淘淘家到学校的路线有:(1)①→②→⑤→⑩;
(2)①→④→⑦→⑩;(3)①→④→⑨→?;(4)③→⑥→⑨→?;(5)③→⑥→⑦→⑩;(6)③→⑧→?→?。
第3课时 搭配(3)
1.
答:一共有10场比赛。
解析 连线如上图。每两个班都要赛一场,从三(1)班开始数,分别与三(2)、三(3)、三(4)、三(5)班赛一场,共四场;三(2)班分别与三(3)、三(4)、三(5)班赛一场,共三场;三(3)班要与三(4)、三(5)班赛一场,共两场;三(4)班与三(5)班赛一场。相加之后的总和为10场。注意避免重复计算。
2.答:一共要下6盘棋。
解析 用A、B、C、D表示这四个同学,用连线的方式数一数。
3.(1)答:共有6种选法。
解析 只需要从4种课程中选出2种课程,与顺序无关,用连线的方式数一数。
(2)答:共有3种选法。
解析 李涵想选的2种课程中有一种百变工程课已确定,另一种课程只能从余下的3种中选出1种,有3种不同的选法。
4.答:一共有10种不同的选法。
解析 只需要考虑选择哪两艘船,与选择这两艘船的顺序无关,用连线法可以直观地表示出来。
5.9
解析 该图既可以从整体上看做一个大的长方形,也可以从横向上看成是两个长方形拼成的一个大长方形。因此要数清楚究竟有多少个长方形,需要数三层:上层、下层和整体。每层都有3个长方形。这样就可以确定,一共有9个长方形。
