人教版八年级数学下册17.1勾股定理同步练习(第2课时 含解析)
文档属性
| 名称 | 人教版八年级数学下册17.1勾股定理同步练习(第2课时 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 233.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-23 00:00:00 | ||
图片预览




文档简介
人教版八年级数学下册17.1勾股定理第2课时同步练习
一.选择题(共6小题)
1.在Rt△ABC中,若斜边AB=3,则AC2+BC2等于( )
A.6 B.9 C.12 D.18
2.如图,学校有一块长方形草地,有极少数人为了避开拐角走“捷径”,在草地内走出了一条“路”,他们仅仅少走了( )米路,却踩伤了花草.
第2题图 第3题图 第4题图
A.1 B.2 C.5 D.12
3.如图,一棵大树在离地面6米高的B处断裂,树顶A落在离树底部C的8米处,则大树断裂之前的高度为( )
A.10米 B.16米 C.15米 D.14米
4.如图,小巷左右两侧是竖直的墙壁,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面1.5米,则小巷的宽度为( )
A.2.7米 B.2.5米 C.2米 D.1.8米
5.如图,架在消防车上的云梯AB长为10m,∠ADB=90°,AD=2BD,云梯底部离地面的距离BC为2m,则云梯的顶端离地面的距离AE为( )
第5题图 第9题图
A.(2+2)m B.(4+2)m C.(5+2)m D.7m
6.如图,小明准备测量一段水渠的深度,他把一根竹竿AB竖直插到水底,此时竹竿AB离岸边点C处的距离CD=1.5米.竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )米.
A.2 B.2.5 C.2.25 D.3
二.填空题(共7小题)
7.在直角坐标系中,点B的坐标是(﹣1,2),则点B到原点的距离是 .
8.如果Rt△ABC是轴对称图形,且斜边AB的长是10cm,则Rt△ABC的面积是 cm2.
9.如图,将一副三角尺按图所示叠放在一起,若AB=6cm,则阴影部分的面积是 cm2.
10.如图,一艘海轮位于灯塔P的北偏东方向60°,距离灯塔为4海里的点A处,如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长 海里.
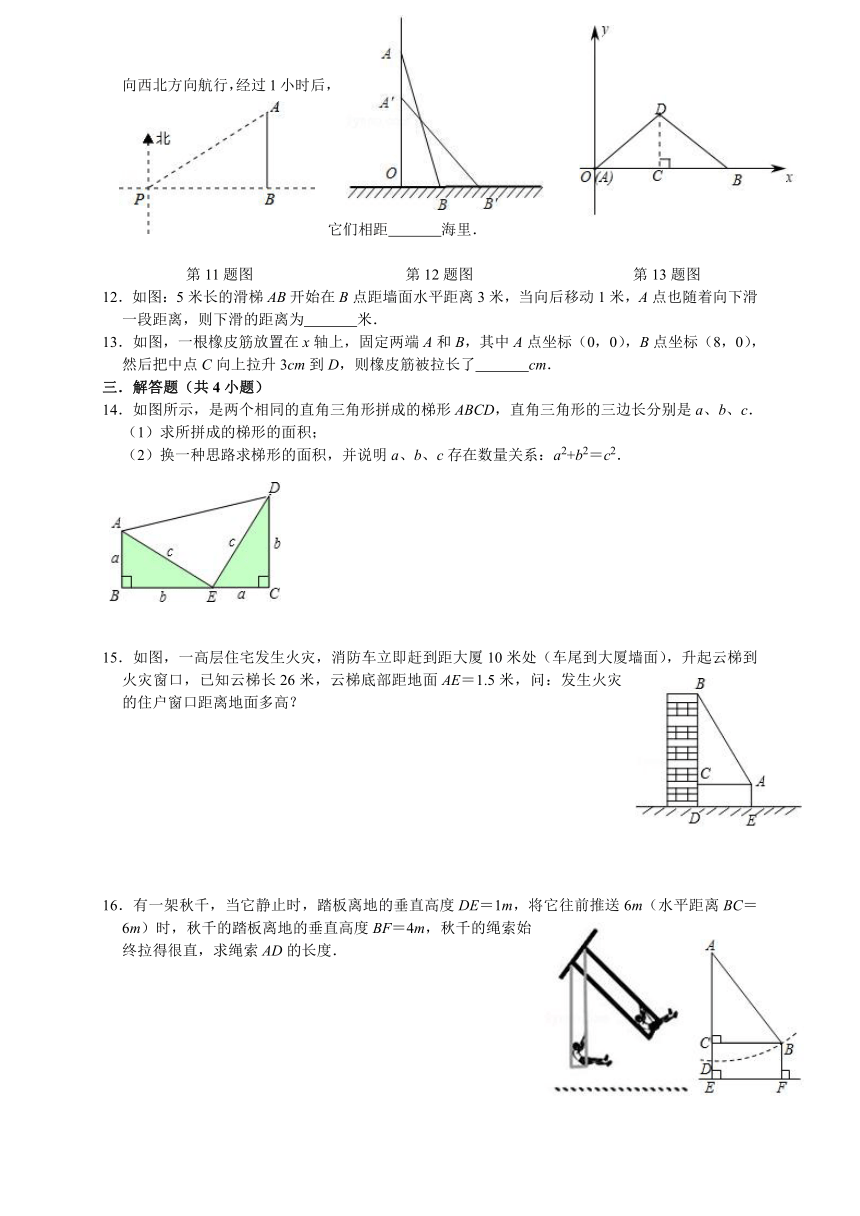
11.一轮船以16海里/时的速度从A港向东北方向航行,另一艘船同时以12海里/时的速度从A港向西北方向航行,经过1小时后,它们相距 海里.
第11题图 第12题图 第13题图
12.如图:5米长的滑梯AB开始在B点距墙面水平距离3米,当向后移动1米,A点也随着向下滑一段距离,则下滑的距离为 米.
13.如图,一根橡皮筋放置在x轴上,固定两端A和B,其中A点坐标(0,0),B点坐标(8,0),然后把中点C向上拉升3cm到D,则橡皮筋被拉长了 cm.
三.解答题(共4小题)
14.如图所示,是两个相同的直角三角形拼成的梯形ABCD,直角三角形的三边长分别是a、b、c.
(1)求所拼成的梯形的面积;
(2)换一种思路求梯形的面积,并说明a、b、c存在数量关系:a2+b2=c2.
15.如图,一高层住宅发生火灾,消防车立即赶到距大厦10米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长26米,云梯底部距地面AE=1.5米,问:发生火灾的住户窗口距离地面多高?
16.有一架秋千,当它静止时,踏板离地的垂直高度DE=1m,将它往前推送6m(水平距离BC=6m)时,秋千的踏板离地的垂直高度BF=4m,秋千的绳索始终拉得很直,求绳索AD的长度.
17.如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m.若拖拉机行驶时,周围100m以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时:
(1)学校是否会受到噪声影响?
(2)如果不受影响,请说明理由;如果受影响,已知拖拉机的速度为18km/h,那么学校受影响的时间为多少秒?
参考答案与试题解析
一.选择题(共6小题)
1.在Rt△ABC中,若斜边AB=3,则AC2+BC2等于( B )
A.6 B.9 C.12 D.18
【解答】解:∵Rt△ABC中,AB为斜边,
∴AC2+BC2=AB2,
∴AB2+AC2=AB2=32=9.
故选:B.
2.如图,学校有一块长方形草地,有极少数人为了避开拐角走“捷径”,在草地内走出了一条“路”,他们仅仅少走了( B )米路,却踩伤了花草.
A.1 B.2 C.5 D.12
【解答】解:由题意可得,直角三角形的斜边为:=5,
则他们仅仅少走了3+4﹣5=2(米).
故选:B.
3.如图,一棵大树在离地面6米高的B处断裂,树顶A落在离树底部C的8米处,则大树断裂之前的高度为( B )
A.10米 B.16米 C.15米 D.14米
【解答】解:由题意得BC=6,在直角三角形ABC中,根据勾股定理得:AB===10米.
所以大树的高度是10+6=16米.
故选:B.
4.如图,小巷左右两侧是竖直的墙壁,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面1.5米,则小巷的宽度为( A )
A.2.7米 B.2.5米 C.2米 D.1.8米
【解答】解:由题意可得:AD2=0.72+2.42=6.25,
在Rt△ABC中,
∵∠ABC=90°,BC=1.5米,BC2+AB2=AC2,
∴AB2+1.52=6.25,
∴AB=±2,
∵AB>0,
∴AB=2米,
∴小巷的宽度为0.7+2=2.7(米).
故选:A.
5.如图,架在消防车上的云梯AB长为10m,∠ADB=90°,AD=2BD,云梯底部离地面的距离BC为2m,则云梯的顶端离地面的距离AE为( B )
A.(2+2)m B.(4+2)m C.(5+2)m D.7m
【解答】解:设AD=x米,
∴BD=0.5x,
∵AB长为10m,
∴AD2+BD2=152,
∴x2+0.25x2=100,
解得:x=4米,
∴AE=AD+DE=(4+2)米,
∴云梯顶端离地面的距离AE为(4+2)米.
故选:B.
6.如图,小明准备测量一段水渠的深度,他把一根竹竿AB竖直插到水底,此时竹竿AB离岸边点C处的距离CD=1.5米.竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( A )米.
A.2 B.2.5 C.2.25 D.3
【解答】解:设BD的长度为xm,则AB=BC=(x+0.5)m,
在Rt△CDB中,1.52+x2=(x+0.5)2,
解得x=2.
故选:A.
二.填空题(共7小题)
7.在直角坐标系中,点B的坐标是(﹣1,2),则点B到原点的距离是 .
【解答】解:点B到原点的距离是=,
故答案为:.
8.如果Rt△ABC是轴对称图形,且斜边AB的长是10cm,则Rt△ABC的面积是 25 cm2.
【解答】解:∵Rt△ABC是轴对称图形,
∴△ABC是等腰直角三角形,
∵斜边AB的长是10cm,
∴直角边长为×10=5(cm),
∴Rt△ABC的面积=×5×5=25(cm2);
故答案为:25.
9.将一副三角尺按图所示叠放在一起,若AB=6cm,则阴影部分的面积是 cm2.
【解答】解:在Rt△ABC中,∵∠ACB=90°,AB=6cm,∠B=30°,
∴AC=AB=3cm,
∵△ADE是等腰直角三角形,
∴∠CAF=45°,
∴∠AFC=∠CAF=45°,
∴AC=CF=3cm,
∴S阴=?CF=cm2,
故答案为
10.如图,一艘海轮位于灯塔P的北偏东方向60°,距离灯塔为4海里的点A处,如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长 2 海里.
【解答】解:如图,由题意可知∠NPA=60°,AP=4海里,∠ABP=90°.
∵AB∥NP,
∴∠A=∠NPA=60°.
在Rt△ABP中,∵∠ABP=90°,∠A=60°,AP=4海里,
∴AB=AP?cos∠A=4×cos60°=4×=2海里.
故答案为2.
11.一轮船以16海里/时的速度从A港向东北方向航行,另一艘船同时以12海里/时的速度从A港向西北方向航行,经过1小时后,它们相距 20 海里.
【解答】解:如图,
∵由图可知AC=16×1=16(海里),
AB=12×1=12(海里),
在Rt△ABC中,BC=(海里).
故它们相距20海里.
故答案为:20
12.如图:5米长的滑梯AB开始在B点距墙面水平距离3米,当向后移动1米,A点也随着向下滑一段距离,则下滑的距离为 1 米.
【解答】解:如上图所示:
在Rt△OAB中,OB=3,AB=5,由勾股定理得:
OA===4,
当向后移动1米,△OAB变为△OA′B′,此时OB′=3+1=4,A′B′=5,
在Rt△OA′B′中,由勾股定理得:
OA′===3,
AA′=OA﹣OA′=4﹣3=1,
所以,下滑的距离等于1m.
13.如图,一根橡皮筋放置在x轴上,固定两端A和B,其中A点坐标(0,0),B点坐标(8,0),然后把中点C向上拉升3cm到D,则橡皮筋被拉长了 2 cm.
【解答】解:Rt△ACD中,AC=AB=4cm,CD=3cm;
根据勾股定理,得:AD===5(cm);
∴AD+BD﹣AB=2AD﹣AB=10﹣8=2cm;
故橡皮筋被拉长了2cm.
故答案是:2.
三.解答题(共4小题)
14.如图所示,是两个相同的直角三角形拼成的梯形ABCD,直角三角形的三边长分别是a、b、c.
(1)求所拼成的梯形的面积;
(2)换一种思路求梯形的面积,并说明a、b、c存在数量关系:a2+b2=c2.
【解答】解:(1)根据梯形面积公式可知:
S梯形ABCD=(a+b)×(a+b),
=(a2+2ab+b2),
=a2+ab+b2;
(2)∵△ABE≌△ECD,
∴∠AEB=∠EDC,
又∵∠EDC+∠DEC=90°,
∴∠AEB+∠EDC=90°,
∴∠AED=180°﹣90°﹣90°,
∴S梯形ABCD=S△ABE+S△ADE+S△DEC=ab+c2+ab=ab+c2,
∴a2+ab+b2=ab+c2,
∴a2+b2=c2.
15.如图,一高层住宅发生火灾,消防车立即赶到距大厦10米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长26米,云梯底部距地面AE=1.5米,问:发生火灾的住户窗口距离地面多高?
【解答】解:∵AC⊥BC,
∴∠ACB=90°;
根据勾股定理,得
BC===24,
∴BD=24+1.5=25.5(米);
答:发生火灾的住户窗口距离地面25.5米.
16.有一架秋千,当它静止时,踏板离地的垂直高度DE=1m,将它往前推送6m(水平距离BC=6m)时,秋千的踏板离地的垂直高度BF=4m,秋千的绳索始终拉得很直,求绳索AD的长度.
【解答】解:在Rt△ACB中,
AC2+BC2=AB2,
设秋千的绳索长为xm,则AC=(x﹣3)m,
故x2=62+(x﹣3)2,
解得:x=7.5,
答:绳索AD的长度是7.5m.
17.如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m.若拖拉机行驶时,周围100m以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时:
(1)学校是否会受到噪声影响?
(2)如果不受影响,请说明理由;如果受影响,已知拖拉机的速度为18km/h,那么学校受影响的时间为多少秒?
【解答】解:(1)作AH⊥MN于H,如图,
在Rt△APH中,
∵∠HPA=30°,
∴AH=AP=×160°=80,
而80<100,
∴拖拉机在公路MN上沿PN方向行驶时学校会受到影响;
(2)以A为圆心,100为半径画弧交MN于B、C,如图,则AB=AC=100,
而AH⊥BC,
∴BH=CH,
在Rt△ABH中,BH==60,
∴BC=2BH=120,
∵拖拉机的速度=18km/h=5m/s,
∴学校受到的影响的时间==24(秒).
一.选择题(共6小题)
1.在Rt△ABC中,若斜边AB=3,则AC2+BC2等于( )
A.6 B.9 C.12 D.18
2.如图,学校有一块长方形草地,有极少数人为了避开拐角走“捷径”,在草地内走出了一条“路”,他们仅仅少走了( )米路,却踩伤了花草.
第2题图 第3题图 第4题图
A.1 B.2 C.5 D.12
3.如图,一棵大树在离地面6米高的B处断裂,树顶A落在离树底部C的8米处,则大树断裂之前的高度为( )
A.10米 B.16米 C.15米 D.14米
4.如图,小巷左右两侧是竖直的墙壁,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面1.5米,则小巷的宽度为( )
A.2.7米 B.2.5米 C.2米 D.1.8米
5.如图,架在消防车上的云梯AB长为10m,∠ADB=90°,AD=2BD,云梯底部离地面的距离BC为2m,则云梯的顶端离地面的距离AE为( )
第5题图 第9题图
A.(2+2)m B.(4+2)m C.(5+2)m D.7m
6.如图,小明准备测量一段水渠的深度,他把一根竹竿AB竖直插到水底,此时竹竿AB离岸边点C处的距离CD=1.5米.竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( )米.
A.2 B.2.5 C.2.25 D.3
二.填空题(共7小题)
7.在直角坐标系中,点B的坐标是(﹣1,2),则点B到原点的距离是 .
8.如果Rt△ABC是轴对称图形,且斜边AB的长是10cm,则Rt△ABC的面积是 cm2.
9.如图,将一副三角尺按图所示叠放在一起,若AB=6cm,则阴影部分的面积是 cm2.
10.如图,一艘海轮位于灯塔P的北偏东方向60°,距离灯塔为4海里的点A处,如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长 海里.
11.一轮船以16海里/时的速度从A港向东北方向航行,另一艘船同时以12海里/时的速度从A港向西北方向航行,经过1小时后,它们相距 海里.
第11题图 第12题图 第13题图
12.如图:5米长的滑梯AB开始在B点距墙面水平距离3米,当向后移动1米,A点也随着向下滑一段距离,则下滑的距离为 米.
13.如图,一根橡皮筋放置在x轴上,固定两端A和B,其中A点坐标(0,0),B点坐标(8,0),然后把中点C向上拉升3cm到D,则橡皮筋被拉长了 cm.
三.解答题(共4小题)
14.如图所示,是两个相同的直角三角形拼成的梯形ABCD,直角三角形的三边长分别是a、b、c.
(1)求所拼成的梯形的面积;
(2)换一种思路求梯形的面积,并说明a、b、c存在数量关系:a2+b2=c2.
15.如图,一高层住宅发生火灾,消防车立即赶到距大厦10米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长26米,云梯底部距地面AE=1.5米,问:发生火灾的住户窗口距离地面多高?
16.有一架秋千,当它静止时,踏板离地的垂直高度DE=1m,将它往前推送6m(水平距离BC=6m)时,秋千的踏板离地的垂直高度BF=4m,秋千的绳索始终拉得很直,求绳索AD的长度.
17.如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m.若拖拉机行驶时,周围100m以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时:
(1)学校是否会受到噪声影响?
(2)如果不受影响,请说明理由;如果受影响,已知拖拉机的速度为18km/h,那么学校受影响的时间为多少秒?
参考答案与试题解析
一.选择题(共6小题)
1.在Rt△ABC中,若斜边AB=3,则AC2+BC2等于( B )
A.6 B.9 C.12 D.18
【解答】解:∵Rt△ABC中,AB为斜边,
∴AC2+BC2=AB2,
∴AB2+AC2=AB2=32=9.
故选:B.
2.如图,学校有一块长方形草地,有极少数人为了避开拐角走“捷径”,在草地内走出了一条“路”,他们仅仅少走了( B )米路,却踩伤了花草.
A.1 B.2 C.5 D.12
【解答】解:由题意可得,直角三角形的斜边为:=5,
则他们仅仅少走了3+4﹣5=2(米).
故选:B.
3.如图,一棵大树在离地面6米高的B处断裂,树顶A落在离树底部C的8米处,则大树断裂之前的高度为( B )
A.10米 B.16米 C.15米 D.14米
【解答】解:由题意得BC=6,在直角三角形ABC中,根据勾股定理得:AB===10米.
所以大树的高度是10+6=16米.
故选:B.
4.如图,小巷左右两侧是竖直的墙壁,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面1.5米,则小巷的宽度为( A )
A.2.7米 B.2.5米 C.2米 D.1.8米
【解答】解:由题意可得:AD2=0.72+2.42=6.25,
在Rt△ABC中,
∵∠ABC=90°,BC=1.5米,BC2+AB2=AC2,
∴AB2+1.52=6.25,
∴AB=±2,
∵AB>0,
∴AB=2米,
∴小巷的宽度为0.7+2=2.7(米).
故选:A.
5.如图,架在消防车上的云梯AB长为10m,∠ADB=90°,AD=2BD,云梯底部离地面的距离BC为2m,则云梯的顶端离地面的距离AE为( B )
A.(2+2)m B.(4+2)m C.(5+2)m D.7m
【解答】解:设AD=x米,
∴BD=0.5x,
∵AB长为10m,
∴AD2+BD2=152,
∴x2+0.25x2=100,
解得:x=4米,
∴AE=AD+DE=(4+2)米,
∴云梯顶端离地面的距离AE为(4+2)米.
故选:B.
6.如图,小明准备测量一段水渠的深度,他把一根竹竿AB竖直插到水底,此时竹竿AB离岸边点C处的距离CD=1.5米.竹竿高出水面的部分AD长0.5米,如果把竹竿的顶端A拉向岸边点C处,竿顶和岸边的水面刚好相齐,则水渠的深度BD为( A )米.
A.2 B.2.5 C.2.25 D.3
【解答】解:设BD的长度为xm,则AB=BC=(x+0.5)m,
在Rt△CDB中,1.52+x2=(x+0.5)2,
解得x=2.
故选:A.
二.填空题(共7小题)
7.在直角坐标系中,点B的坐标是(﹣1,2),则点B到原点的距离是 .
【解答】解:点B到原点的距离是=,
故答案为:.
8.如果Rt△ABC是轴对称图形,且斜边AB的长是10cm,则Rt△ABC的面积是 25 cm2.
【解答】解:∵Rt△ABC是轴对称图形,
∴△ABC是等腰直角三角形,
∵斜边AB的长是10cm,
∴直角边长为×10=5(cm),
∴Rt△ABC的面积=×5×5=25(cm2);
故答案为:25.
9.将一副三角尺按图所示叠放在一起,若AB=6cm,则阴影部分的面积是 cm2.
【解答】解:在Rt△ABC中,∵∠ACB=90°,AB=6cm,∠B=30°,
∴AC=AB=3cm,
∵△ADE是等腰直角三角形,
∴∠CAF=45°,
∴∠AFC=∠CAF=45°,
∴AC=CF=3cm,
∴S阴=?CF=cm2,
故答案为
10.如图,一艘海轮位于灯塔P的北偏东方向60°,距离灯塔为4海里的点A处,如果海轮沿正南方向航行到灯塔的正东位置,海轮航行的距离AB长 2 海里.
【解答】解:如图,由题意可知∠NPA=60°,AP=4海里,∠ABP=90°.
∵AB∥NP,
∴∠A=∠NPA=60°.
在Rt△ABP中,∵∠ABP=90°,∠A=60°,AP=4海里,
∴AB=AP?cos∠A=4×cos60°=4×=2海里.
故答案为2.
11.一轮船以16海里/时的速度从A港向东北方向航行,另一艘船同时以12海里/时的速度从A港向西北方向航行,经过1小时后,它们相距 20 海里.
【解答】解:如图,
∵由图可知AC=16×1=16(海里),
AB=12×1=12(海里),
在Rt△ABC中,BC=(海里).
故它们相距20海里.
故答案为:20
12.如图:5米长的滑梯AB开始在B点距墙面水平距离3米,当向后移动1米,A点也随着向下滑一段距离,则下滑的距离为 1 米.
【解答】解:如上图所示:
在Rt△OAB中,OB=3,AB=5,由勾股定理得:
OA===4,
当向后移动1米,△OAB变为△OA′B′,此时OB′=3+1=4,A′B′=5,
在Rt△OA′B′中,由勾股定理得:
OA′===3,
AA′=OA﹣OA′=4﹣3=1,
所以,下滑的距离等于1m.
13.如图,一根橡皮筋放置在x轴上,固定两端A和B,其中A点坐标(0,0),B点坐标(8,0),然后把中点C向上拉升3cm到D,则橡皮筋被拉长了 2 cm.
【解答】解:Rt△ACD中,AC=AB=4cm,CD=3cm;
根据勾股定理,得:AD===5(cm);
∴AD+BD﹣AB=2AD﹣AB=10﹣8=2cm;
故橡皮筋被拉长了2cm.
故答案是:2.
三.解答题(共4小题)
14.如图所示,是两个相同的直角三角形拼成的梯形ABCD,直角三角形的三边长分别是a、b、c.
(1)求所拼成的梯形的面积;
(2)换一种思路求梯形的面积,并说明a、b、c存在数量关系:a2+b2=c2.
【解答】解:(1)根据梯形面积公式可知:
S梯形ABCD=(a+b)×(a+b),
=(a2+2ab+b2),
=a2+ab+b2;
(2)∵△ABE≌△ECD,
∴∠AEB=∠EDC,
又∵∠EDC+∠DEC=90°,
∴∠AEB+∠EDC=90°,
∴∠AED=180°﹣90°﹣90°,
∴S梯形ABCD=S△ABE+S△ADE+S△DEC=ab+c2+ab=ab+c2,
∴a2+ab+b2=ab+c2,
∴a2+b2=c2.
15.如图,一高层住宅发生火灾,消防车立即赶到距大厦10米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长26米,云梯底部距地面AE=1.5米,问:发生火灾的住户窗口距离地面多高?
【解答】解:∵AC⊥BC,
∴∠ACB=90°;
根据勾股定理,得
BC===24,
∴BD=24+1.5=25.5(米);
答:发生火灾的住户窗口距离地面25.5米.
16.有一架秋千,当它静止时,踏板离地的垂直高度DE=1m,将它往前推送6m(水平距离BC=6m)时,秋千的踏板离地的垂直高度BF=4m,秋千的绳索始终拉得很直,求绳索AD的长度.
【解答】解:在Rt△ACB中,
AC2+BC2=AB2,
设秋千的绳索长为xm,则AC=(x﹣3)m,
故x2=62+(x﹣3)2,
解得:x=7.5,
答:绳索AD的长度是7.5m.
17.如图,公路MN和公路PQ在点P处交汇,且∠QPN=30°,点A处有一所中学,AP=160m.若拖拉机行驶时,周围100m以内会受到噪音的影响,那么拖拉机在公路MN上沿PN方向行驶时:
(1)学校是否会受到噪声影响?
(2)如果不受影响,请说明理由;如果受影响,已知拖拉机的速度为18km/h,那么学校受影响的时间为多少秒?
【解答】解:(1)作AH⊥MN于H,如图,
在Rt△APH中,
∵∠HPA=30°,
∴AH=AP=×160°=80,
而80<100,
∴拖拉机在公路MN上沿PN方向行驶时学校会受到影响;
(2)以A为圆心,100为半径画弧交MN于B、C,如图,则AB=AC=100,
而AH⊥BC,
∴BH=CH,
在Rt△ABH中,BH==60,
∴BC=2BH=120,
∵拖拉机的速度=18km/h=5m/s,
∴学校受到的影响的时间==24(秒).
