人教版八年级数学下册:17.1勾股定理 同步练习(解析版)
文档属性
| 名称 | 人教版八年级数学下册:17.1勾股定理 同步练习(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 115.2KB | ||
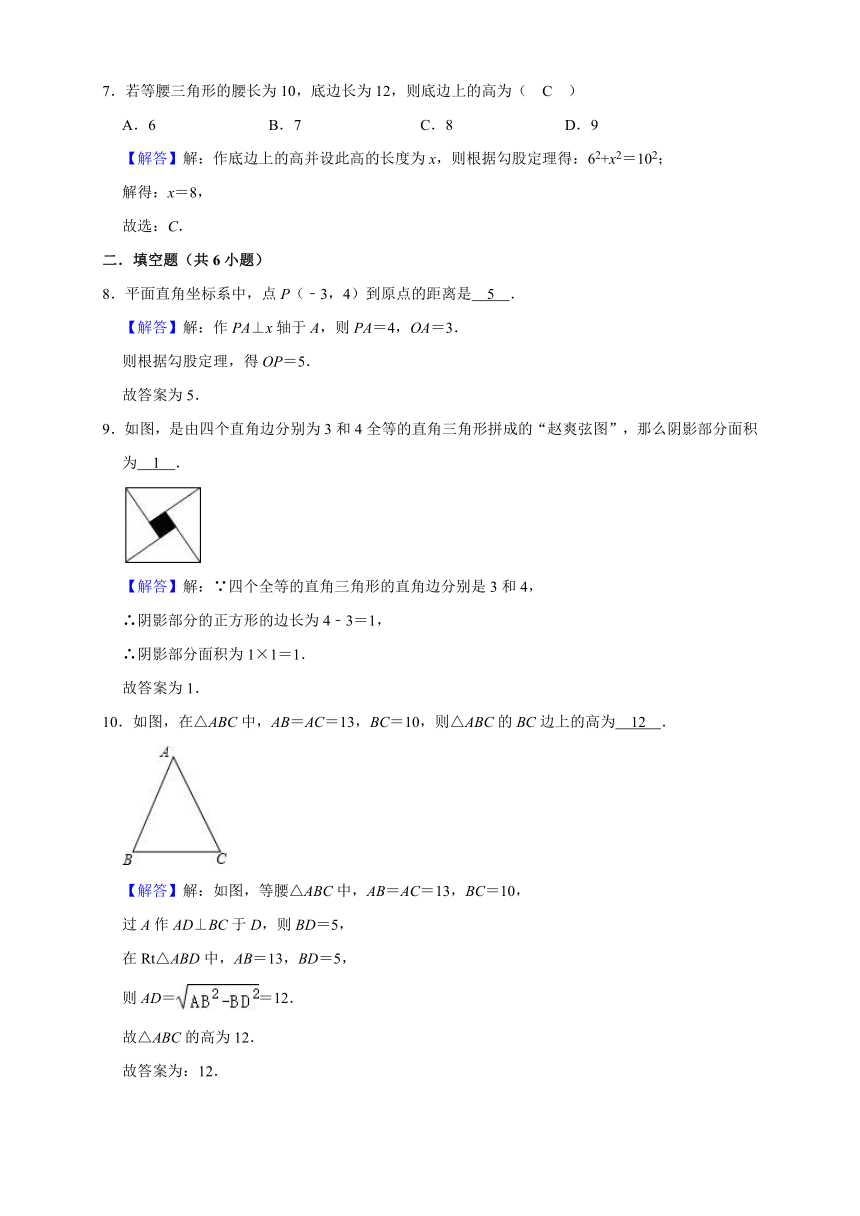
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-23 00:00:00 | ||
图片预览

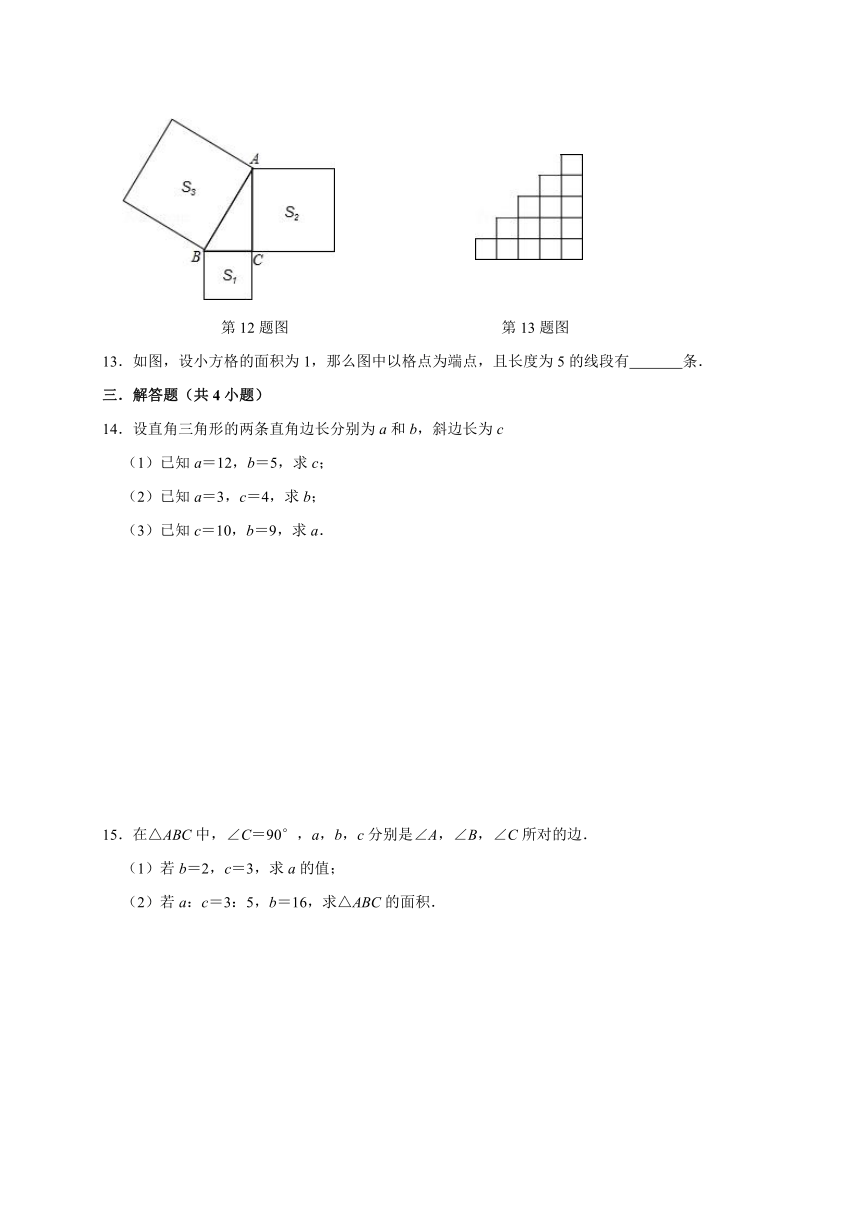


文档简介
人教版八年级数学下册17.1勾股定理第1课时同步练习
一.选择题(共7小题)
1.直角三角形两条直角边的长分别为3和4,则斜边长为( )
A.4 B.5 C.6 D.10
2.直角三角形的两直角边的长分别为5和12,则第三边长为( )
A.10 B.13 C.15 D.17
3.若一直角三角形两边长为4和5,则第三边长为( )
A.3 B. C.3或 D.不确定
4.如图是一个直角三角形,它的未知边的长x等于( )
A.13 B. C.5 D.
5.小明用火柴棒摆直角三角形,已知他摆两条直角边分别用了6根和8根火柴棒,他摆完这个直角三角形共用火柴棒( )
A.20根 B.14根 C.24根 D.30根
6.如右图:直角三角形的三边为边向外作三个正方形,则图形A的面积是( )
A.225 B.144 C.81 D.无法确定
7.若等腰三角形的腰长为10,底边长为12,则底边上的高为( )
A.6 B.7 C.8 D.9
二.填空题(共6小题)
8.平面直角坐标系中,点P(﹣3,4)到原点的距离是 .
9.如图,是由四个直角边分别为3和4全等的直角三角形拼成的“赵爽弦图”,那么阴影部分面积为 .
第9题图 第10题图 第11题图
10.如图,在△ABC中,AB=AC=13,BC=10,则△ABC中BC边上的高为 .
11.如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=2,则点A的坐标为 .
12.如图,以Rt△ABC的三边为边向外作三个正方形,其面积S1=4,S2=8,则S3= .
第12题图 第13题图
13.如图,设小方格的面积为1,那么图中以格点为端点,且长度为5的线段有 条.
三.解答题(共4小题)
14.设直角三角形的两条直角边长分别为a和b,斜边长为c
(1)已知a=12,b=5,求c;
(2)已知a=3,c=4,求b;
(3)已知c=10,b=9,求a.
15.在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C所对的边.
(1)若b=2,c=3,求a的值;
(2)若a:c=3:5,b=16,求△ABC的面积.
16.已知,如图,在△ABC中.∠C=90°,AD平分∠BAC.
(1)若BC=16,BD=10.求点D到AB的距离:
(2)若BC=8,BD:CD=5:3,AB=10,求△ABD的面积.
17.如图所示,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△EDB的面积.
参考答案与试题解析
一.选择题(共7小题)
1.直角三角形两条直角边的长分别为3和4,则斜边长为( B )
A.4 B.5 C.6 D.10
【解答】解:由勾股定理得:斜边长为:=5.
故选:B.
2.直角三角形的两直角边的长分别为5和12,则第三边长为( B )
A.10 B.13 C.15 D.17
【解答】解:第三边的长是=13.故选B.
3.若一直角三角形两边长为4和5,则第三边长为( C )
A.3 B. C.3或 D.不确定
【解答】解:当5是直角边时,则第三边==;
当5是斜边时,则第三边==3.
综上所述,第三边的长是或3.
故选:C.
4.如图是一个直角三角形,它的未知边的长x等于( B )
A.13 B. C.5 D.
【解答】解:∵x==,
故选:B.
5.小明用火柴棒摆直角三角形,已知他摆两条直角边分别用了6根和8根火柴棒,他摆完这个直角三角形共用火柴棒( C )
A.20根 B.14根 C.24根 D.30根
【解答】解:∵两直角边分别用了6根、8根长度相同的火柴棒
∴由勾股定理,得到斜边需用:=10(根),
∴他摆完这个直角三角形共用火柴棒是:6+8+10=24.
故选:C.
6.如图:图形A的面积是( C )
A.225 B.144 C.81 D.无法确定
【解答】解:由勾股定理得,A的面积=225﹣144=81.
故选:C.
7.若等腰三角形的腰长为10,底边长为12,则底边上的高为( C )
A.6 B.7 C.8 D.9
【解答】解:作底边上的高并设此高的长度为x,则根据勾股定理得:62+x2=102;
解得:x=8,
故选:C.
二.填空题(共6小题)
8.平面直角坐标系中,点P(﹣3,4)到原点的距离是 5 .
【解答】解:作PA⊥x轴于A,则PA=4,OA=3.
则根据勾股定理,得OP=5.
故答案为5.
9.如图,是由四个直角边分别为3和4全等的直角三角形拼成的“赵爽弦图”,那么阴影部分面积为 1 .
【解答】解:∵四个全等的直角三角形的直角边分别是3和4,
∴阴影部分的正方形的边长为4﹣3=1,
∴阴影部分面积为1×1=1.
故答案为1.
10.如图,在△ABC中,AB=AC=13,BC=10,则△ABC的BC边上的高为 12 .
【解答】解:如图,等腰△ABC中,AB=AC=13,BC=10,
过A作AD⊥BC于D,则BD=5,
在Rt△ABD中,AB=13,BD=5,
则AD==12.
故△ABC的高为12.
故答案为:12.
11.如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=2,则点A的坐标为 (1,) .
【解答】解:过点A作AC⊥OB,
∵△AOB是等边三角形,
∴OA=OB,OC=BC,
∠AOB=60°,
∵点B的坐标为(2,0),
∴OB=2,
∴OA=2,
∴OC=1,
∴AC=,
∴点A的坐标是(1,).
故答案是:(1,).
12.如图,以Rt△ABC的三边为边向外作三个正方形,其面积S1=4,S2=8,则S3= 12 .
【解答】解:∵由勾股定理得:BC2+AC2=AB2,
∴S1+S2=S3,
∴S3=4+8=12,
故答案为:12.
13.如图,设小方格的面积为1,那么图中以格点为端点,且长度为5的线段有 14 条.
【解答】解:如图所示:10条斜线,4条直线.共14条.
故答案是:14.
三.解答题(共4小题)
14.设直角三角形的两条直角边长分别为a和b,斜边长为c
(1)已知a=12,b=5,求c;
(2)已知a=3,c=4,求b;
(3)已知c=10,b=9,求a.
【解答】解:(1)∵直角三角形的两条直角边长分别为a和b,斜边长为c,a=12,b=5,
∴c===13;
(2)∵直角三角形的两条直角边长分别为a和b,斜边长为c,a=3,c=4,
∴b===;
(3)∵直角三角形的两条直角边长分别为a和b,斜边长为c,c=10,b=9,
∴a===.
15.在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C所对的边.
(1)若b=2,c=3,求a的值;
(2)若a:c=3:5,b=16,求△ABC的面积.
【解答】解:
(1)∵△ABC中,∠C=90°,b=2,c=3,
∴a==;
(2)∵a:c=3:5,
∴设a=3x,c=5x,
∵b=16,
∴9x2+162=25x2,
解得:x=4,
∴a=12,
∴△ABC的面积=×12×16=96.
16.已知,如图,在△ABC中.∠C=90°,AD平分∠BAC.
(1)若BC=16,BD=10.求点D到AB的距离:
(2)若BC=8,BD:CD=5:3,AB=10,求△ABD的面积.
【解答】解:(1)∵在△ABC中,∠C=90°,
∴DC⊥AC,
∵BC=16,BD=10,
∴CD=16﹣10=6,
∵AD平分∠BAC.
∴点D到AB的距离=CD=6.
(2)∵在△ABC中,∠C=90°,
∴DC⊥AC,
∵BC=8,BD:CD=5:3,
∴BD=5,CD=3,
∵AB=10,
∴AC==6,
∴△ABD的面积=BD?AC=15.
17.如图所示,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△EDB的面积.
【解答】解:(1)∵∠C=90°,AD平分∠CAB,DE⊥AB,
∴DE=CD,
∵CD=3,
∴DE=3;
(2)∵∠C=90°,AC=6,BC=8,
∴AB==10,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC=6,
∴BE=AB﹣AE=10﹣6=4,
∴△BDE的面积=DE?BE=×3×4=6.
一.选择题(共7小题)
1.直角三角形两条直角边的长分别为3和4,则斜边长为( )
A.4 B.5 C.6 D.10
2.直角三角形的两直角边的长分别为5和12,则第三边长为( )
A.10 B.13 C.15 D.17
3.若一直角三角形两边长为4和5,则第三边长为( )
A.3 B. C.3或 D.不确定
4.如图是一个直角三角形,它的未知边的长x等于( )
A.13 B. C.5 D.
5.小明用火柴棒摆直角三角形,已知他摆两条直角边分别用了6根和8根火柴棒,他摆完这个直角三角形共用火柴棒( )
A.20根 B.14根 C.24根 D.30根
6.如右图:直角三角形的三边为边向外作三个正方形,则图形A的面积是( )
A.225 B.144 C.81 D.无法确定
7.若等腰三角形的腰长为10,底边长为12,则底边上的高为( )
A.6 B.7 C.8 D.9
二.填空题(共6小题)
8.平面直角坐标系中,点P(﹣3,4)到原点的距离是 .
9.如图,是由四个直角边分别为3和4全等的直角三角形拼成的“赵爽弦图”,那么阴影部分面积为 .
第9题图 第10题图 第11题图
10.如图,在△ABC中,AB=AC=13,BC=10,则△ABC中BC边上的高为 .
11.如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=2,则点A的坐标为 .
12.如图,以Rt△ABC的三边为边向外作三个正方形,其面积S1=4,S2=8,则S3= .
第12题图 第13题图
13.如图,设小方格的面积为1,那么图中以格点为端点,且长度为5的线段有 条.
三.解答题(共4小题)
14.设直角三角形的两条直角边长分别为a和b,斜边长为c
(1)已知a=12,b=5,求c;
(2)已知a=3,c=4,求b;
(3)已知c=10,b=9,求a.
15.在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C所对的边.
(1)若b=2,c=3,求a的值;
(2)若a:c=3:5,b=16,求△ABC的面积.
16.已知,如图,在△ABC中.∠C=90°,AD平分∠BAC.
(1)若BC=16,BD=10.求点D到AB的距离:
(2)若BC=8,BD:CD=5:3,AB=10,求△ABD的面积.
17.如图所示,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△EDB的面积.
参考答案与试题解析
一.选择题(共7小题)
1.直角三角形两条直角边的长分别为3和4,则斜边长为( B )
A.4 B.5 C.6 D.10
【解答】解:由勾股定理得:斜边长为:=5.
故选:B.
2.直角三角形的两直角边的长分别为5和12,则第三边长为( B )
A.10 B.13 C.15 D.17
【解答】解:第三边的长是=13.故选B.
3.若一直角三角形两边长为4和5,则第三边长为( C )
A.3 B. C.3或 D.不确定
【解答】解:当5是直角边时,则第三边==;
当5是斜边时,则第三边==3.
综上所述,第三边的长是或3.
故选:C.
4.如图是一个直角三角形,它的未知边的长x等于( B )
A.13 B. C.5 D.
【解答】解:∵x==,
故选:B.
5.小明用火柴棒摆直角三角形,已知他摆两条直角边分别用了6根和8根火柴棒,他摆完这个直角三角形共用火柴棒( C )
A.20根 B.14根 C.24根 D.30根
【解答】解:∵两直角边分别用了6根、8根长度相同的火柴棒
∴由勾股定理,得到斜边需用:=10(根),
∴他摆完这个直角三角形共用火柴棒是:6+8+10=24.
故选:C.
6.如图:图形A的面积是( C )
A.225 B.144 C.81 D.无法确定
【解答】解:由勾股定理得,A的面积=225﹣144=81.
故选:C.
7.若等腰三角形的腰长为10,底边长为12,则底边上的高为( C )
A.6 B.7 C.8 D.9
【解答】解:作底边上的高并设此高的长度为x,则根据勾股定理得:62+x2=102;
解得:x=8,
故选:C.
二.填空题(共6小题)
8.平面直角坐标系中,点P(﹣3,4)到原点的距离是 5 .
【解答】解:作PA⊥x轴于A,则PA=4,OA=3.
则根据勾股定理,得OP=5.
故答案为5.
9.如图,是由四个直角边分别为3和4全等的直角三角形拼成的“赵爽弦图”,那么阴影部分面积为 1 .
【解答】解:∵四个全等的直角三角形的直角边分别是3和4,
∴阴影部分的正方形的边长为4﹣3=1,
∴阴影部分面积为1×1=1.
故答案为1.
10.如图,在△ABC中,AB=AC=13,BC=10,则△ABC的BC边上的高为 12 .
【解答】解:如图,等腰△ABC中,AB=AC=13,BC=10,
过A作AD⊥BC于D,则BD=5,
在Rt△ABD中,AB=13,BD=5,
则AD==12.
故△ABC的高为12.
故答案为:12.
11.如图,在平面直角坐标系中,点B在x轴上,△AOB是等边三角形,AB=2,则点A的坐标为 (1,) .
【解答】解:过点A作AC⊥OB,
∵△AOB是等边三角形,
∴OA=OB,OC=BC,
∠AOB=60°,
∵点B的坐标为(2,0),
∴OB=2,
∴OA=2,
∴OC=1,
∴AC=,
∴点A的坐标是(1,).
故答案是:(1,).
12.如图,以Rt△ABC的三边为边向外作三个正方形,其面积S1=4,S2=8,则S3= 12 .
【解答】解:∵由勾股定理得:BC2+AC2=AB2,
∴S1+S2=S3,
∴S3=4+8=12,
故答案为:12.
13.如图,设小方格的面积为1,那么图中以格点为端点,且长度为5的线段有 14 条.
【解答】解:如图所示:10条斜线,4条直线.共14条.
故答案是:14.
三.解答题(共4小题)
14.设直角三角形的两条直角边长分别为a和b,斜边长为c
(1)已知a=12,b=5,求c;
(2)已知a=3,c=4,求b;
(3)已知c=10,b=9,求a.
【解答】解:(1)∵直角三角形的两条直角边长分别为a和b,斜边长为c,a=12,b=5,
∴c===13;
(2)∵直角三角形的两条直角边长分别为a和b,斜边长为c,a=3,c=4,
∴b===;
(3)∵直角三角形的两条直角边长分别为a和b,斜边长为c,c=10,b=9,
∴a===.
15.在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C所对的边.
(1)若b=2,c=3,求a的值;
(2)若a:c=3:5,b=16,求△ABC的面积.
【解答】解:
(1)∵△ABC中,∠C=90°,b=2,c=3,
∴a==;
(2)∵a:c=3:5,
∴设a=3x,c=5x,
∵b=16,
∴9x2+162=25x2,
解得:x=4,
∴a=12,
∴△ABC的面积=×12×16=96.
16.已知,如图,在△ABC中.∠C=90°,AD平分∠BAC.
(1)若BC=16,BD=10.求点D到AB的距离:
(2)若BC=8,BD:CD=5:3,AB=10,求△ABD的面积.
【解答】解:(1)∵在△ABC中,∠C=90°,
∴DC⊥AC,
∵BC=16,BD=10,
∴CD=16﹣10=6,
∵AD平分∠BAC.
∴点D到AB的距离=CD=6.
(2)∵在△ABC中,∠C=90°,
∴DC⊥AC,
∵BC=8,BD:CD=5:3,
∴BD=5,CD=3,
∵AB=10,
∴AC==6,
∴△ABD的面积=BD?AC=15.
17.如图所示,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8,CD=3.
(1)求DE的长;
(2)求△EDB的面积.
【解答】解:(1)∵∠C=90°,AD平分∠CAB,DE⊥AB,
∴DE=CD,
∵CD=3,
∴DE=3;
(2)∵∠C=90°,AC=6,BC=8,
∴AB==10,
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC=6,
∴BE=AB﹣AE=10﹣6=4,
∴△BDE的面积=DE?BE=×3×4=6.
