2020春北师大版八下数学4.3公式法教学课件(共2课时、32张ppt)
文档属性
| 名称 | 2020春北师大版八下数学4.3公式法教学课件(共2课时、32张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 191.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-24 19:46:36 | ||
图片预览







文档简介
(共32张PPT)
第四章
因式分解
3
公式法(一)
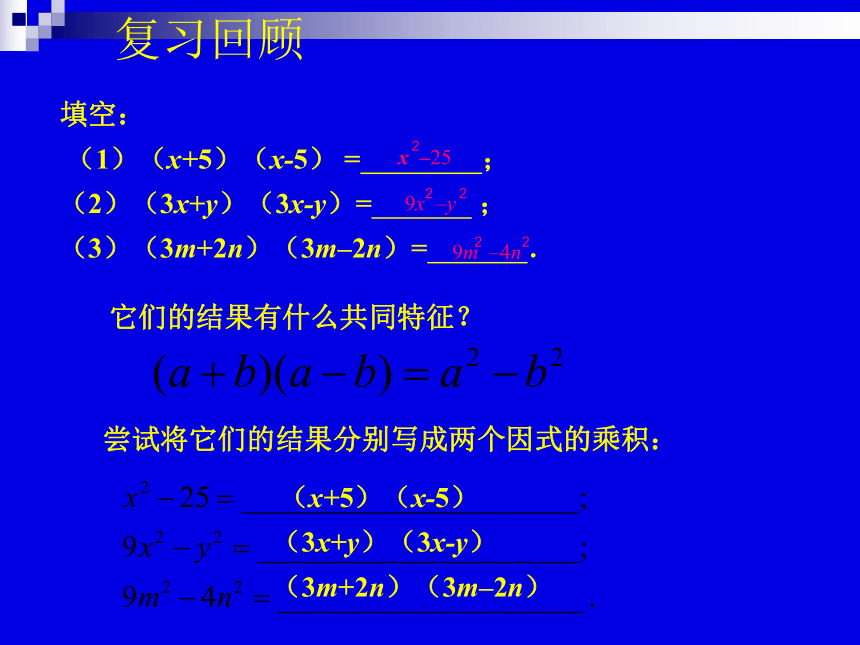
填空:
(1)(x+5)(x-5)
=
;
(2)(3x+y)(3x-y)=
;
(3)(3m+2n)(3m–2n)=
.
它们的结果有什么共同特征?
x
–25
2
2
2
9m
–4n
9x
–y
2
2
复习回顾
尝试将它们的结果分别写成两个因式的乘积:
(x+5)(x-5)
(3x+y)(3x-y)
(3m+2n)(3m–2n)
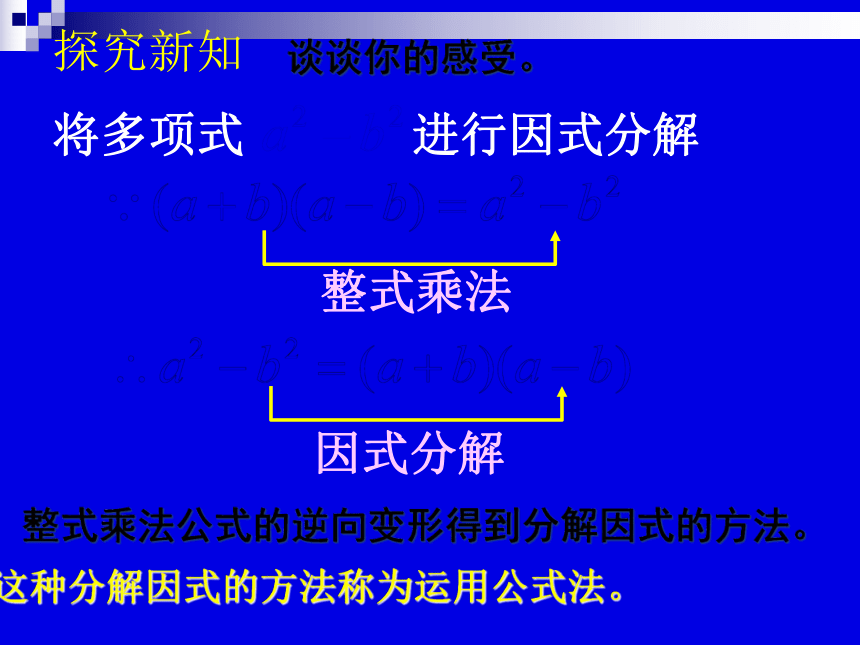
将多项式
进行因式分解
因式分解
整式乘法
探究新知
谈谈你的感受。
整式乘法公式的逆向变形得到分解因式的方法。
这种分解因式的方法称为运用公式法。
(1)公式左边:
(是一个将要被分解因式的多项式)
★被分解的多项式含有两项,且这两项异号,并且能写成( )2-( )2的形式。
(2)
公式右边:
(是分解因式的结果)
★分解的结果是两个底数的和乘以两个底数的差的形式。
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
▲
▲
▲
说一说
找特征
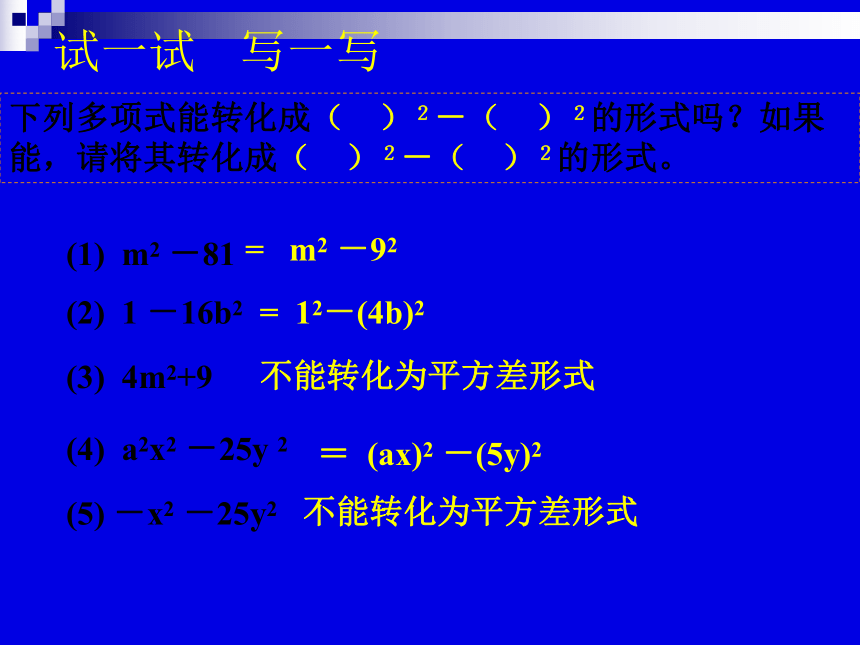
下列多项式能转化成( )2-( )2的形式吗?如果能,请将其转化成( )2-( )2的形式。
(1)
m2
-81
(2)
1
-16b2
(3)
4m2+9
(4)
a2x2
-25y
2
(5)
-x2
-25y2
=
m2
-92
=
12-(4b)2
不能转化为平方差形式
=
(ax)2
-(5y)2
不能转化为平方差形式
试一试
写一写
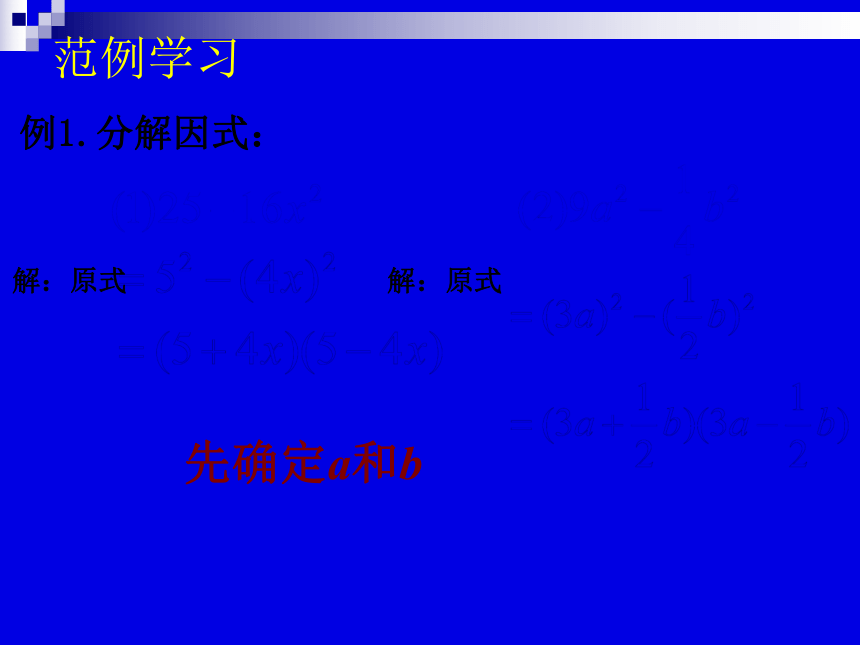
例1.分解因式:
先确定a和b
范例学习
解:原式
解:原式
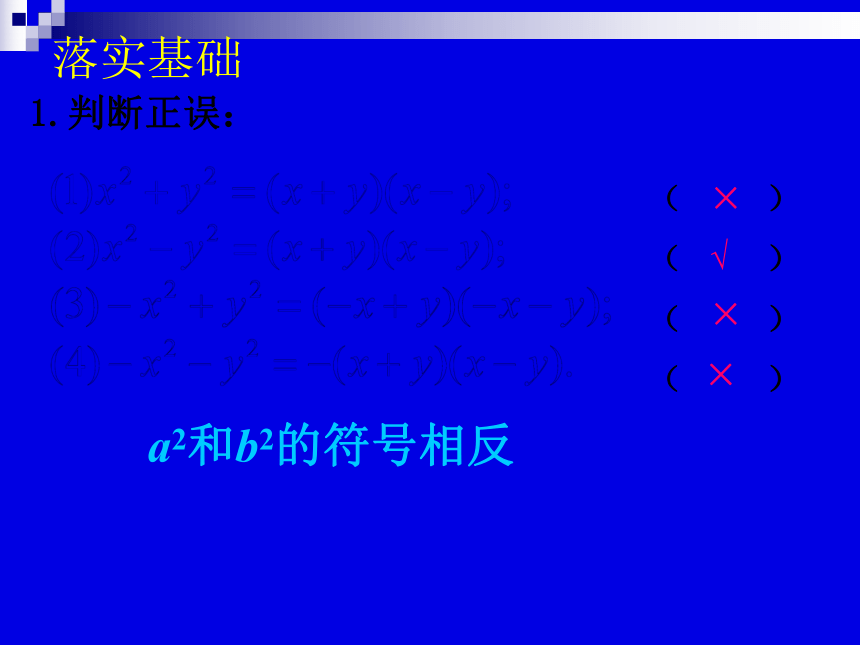
1.判断正误:
a2和b2的符号相反
落实基础
(
)
(
)
(
)
(
)
√
×
×
×
2.分解因式:
分解因式需“彻底”!
把括号看作一个整体
能力提升
例2.分解因式:
解:原式
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
结论:
公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解。
解:原式
方法:
先考虑能否用提取公因式法,再考虑能否用平方差公式分解因式。
解:原式
结论:
分解因式的一般步骤:一提二套
多项式的因式分解要分解到不能再分解为止。
巩固练习
1.把下列各式分解因式:
2.简便计算:
利用因式分解计算
例3.如图,在一块长为a的正方形纸片的四角,各剪去一个边长
为b的正方形.用a
与b表示剩余部分的面积,并求当a=3.6,
b=0.8时的面积.
联系拓广
解:a2-4b2
=(a+2b)(a-2b)cm2
当a=3.6,b=0.8时,
原式=(3.6+2×0.8)
(3.6-2×0.8)
=5.2×2
=10.4cm2
如图,大小两圆的圆心相同,已知它们的半径分别是R
cm和r
cm,求它们所围成的环形的面积。如果R=8.45cm,r=3.45cm呢?
问题解决
解:
R2-
r2
=
(R+r)(R-r)cm2
当R=8.45,r=3.45时,
原式=(8.45+3.45)
×(8.45-3.45)
×3.14
=186.83cm2
自主小结
从今天的课程中,你学到了哪些知识?
掌握了哪些方法?
(1)有公因式(包括负号)则先提取公因式;
(2)整式乘法的平方差公式与因式分解的平方差公式是互逆关系;
(3)平方差公式中的a与b既可以是单项式,又可以是多项式;
作业
完成课本习题
拓展作业:
你能尝试运用今天所学的知识解决下面的问题吗
你知道992-1能否被100整除吗?
如图,在边长为6.8cm正方形钢板上,挖去4个边长为1.6cm的小正方形,求剩余部分的面积。
再攀高峰
第四章
因式分解
3
公式法(二)
一、确定公因式的方法:
提公因式法(复习)
1、公因式的系数是多项式各项__________________;
2、字母取多项式各项中都含有的____________;
3、相同字母的指数取各项中最小的一个,即_________.
系数的最大公约数
相同的字母
最低次幂
二、提公因式法分解因式步骤
(两步):
第一步,找出公因式;
第二步,提公因式,(即用多项式除
以公因式).
公因式
是多项式形式,怎样运用提公因式法分解因式?
想一想
在下列各式等号右边的括号前填入“+”或“-”号,使等式成立:
(a-b)
=___(b-a);
(2)
(a-b)2
=___(b-a)2;
(3)
(a-b)3
=___(b-a)3;
(4)
(a-b)4
=___(b-a)4;
(5)
(a+b)5
=___(b+a)5;
(6)
(a+b)6
=___(b+a)6.
+
-
-
+
+
+
(7)
(a+b)
=___(-b-a);
-
(8)
(a+b)2
=___(-a-b)2.
+
做一做p97
填空
由此可知规律:
(1)a-b
与
-a+b
互为相反数.
(a-b)n
=
(b-a)n
(n是偶数)
(a-b)n
=
-(b-a)n
(n是奇数)
(2)
a+b与b+a
互为相同数,
(a+b)n
=
(b+a)n
(n是整数)
a+b
与
-a-b
互为相反数.
(-a-b)n
=
(a+b)n
(n是偶数)
(-a-b)n
=
-(a+b)n
(n是奇数)
练习一
1.在下列各式右边括号前添上适当的符号,使左边与右边相等.
(1)
a+2
=
___(2+a)
(2)
-x+2y
=
___(2y-x)
(3)
(m-a)2
=
___(a-m)2
(4)
(a-b)3
=
___(-a+b)3
(5)
(x+y)(x-2y)=
___(y+x)(2y-x)
+
+
+
-
-
2.判断下列各式是否正确
(1)
(y-x)2
=
-(x-y)2
(2)
(3+2x)3
=
-(2x+3)3
(3)
a-2b
=
-(-2b+a)
(4)
-a+b
=
-(a+b)
(5)
(a-b)(x-2y)
=
(b-a)(2y-x)
否
否
否
否
对
例1.把
a(x-3)+2b(x-3)
分解因式.
解:
a(x-3)+2b(x-3)
=(x-3)(a+2b)
分析:多项式可看成
a(x-3)
与
2b(x-3)
两项。
公因式为x-3
例题解析
例2.
把a(x-y)+b(y-x)分解因式.
解:
a(x-y)+b(y-x)
=a(x-y)-b(x-y)
=(x-y)(a-b)
分析:多项式可看成a(x-y)与+b(y-x)两项。其中X-y与y-x互为相反数,可将+b(y-x)变为-b(x-y),则a(x-y)与-b(x-y)
公因式为
x-y
例3.
把6(m-n)3-12(n-m)2分解因式.
解:6(m-n)3-12(n-m)2
=
6(m-n)3-12(m-n)2
=
6(m-n)2(m-n-2)
分析:其中(m-n)与(n-m)互为相反数.可将-12(n-m)
2变为-12(m-n)2,则6(m-n)3与-12(m-n)2
公因式为6(m-n)2
例4.把6(x+y)(y-x)2-9(x-y)3分解因式.
解:
6(x+y)(y-x)2-
9(x-y)3
=
6(x+y)(x-y)2-
9(x-y)3
=
3(x-y)2[2(x+y)-3(x-y)]
=
3(x-y)2(2x+2y-3x+3y)
=
3(x-y)2(-x+5y)
=3(x-y)2(5y-x)
(2)
5x(a-b)2+10y(b-a)2
)
3
(
2
3
)
(
12
)
(
6
m
n
n
m
-
-
-
)
1
(
(
(
)
x
y
b
-
-
)
y
x
a
-
分解因式:
(4)
a(a+b)(a-b)-a(a+b)2
(5)
mn(m+n)-m(n+m)2
(6)
2(a-3)2-a+3
(7)
a(x-a)+b(a-x)-c(x-a)
练习二
课堂小结
两个只有符号不同的多项式是否有关系,有如下判断方法:
(1)当相同字母前的符号相同时,
则两个多项式相等.
如:
a-b
和
-b+a
即
a-b
=
-b+a
(2)当相同字母前的符号均相反时,
则两个多项式互为相反数.
如:
a-b
和
b-a
即
a-b
=
-(a-b)
第四章
因式分解
3
公式法(一)
填空:
(1)(x+5)(x-5)
=
;
(2)(3x+y)(3x-y)=
;
(3)(3m+2n)(3m–2n)=
.
它们的结果有什么共同特征?
x
–25
2
2
2
9m
–4n
9x
–y
2
2
复习回顾
尝试将它们的结果分别写成两个因式的乘积:
(x+5)(x-5)
(3x+y)(3x-y)
(3m+2n)(3m–2n)
将多项式
进行因式分解
因式分解
整式乘法
探究新知
谈谈你的感受。
整式乘法公式的逆向变形得到分解因式的方法。
这种分解因式的方法称为运用公式法。
(1)公式左边:
(是一个将要被分解因式的多项式)
★被分解的多项式含有两项,且这两项异号,并且能写成( )2-( )2的形式。
(2)
公式右边:
(是分解因式的结果)
★分解的结果是两个底数的和乘以两个底数的差的形式。
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
▲
▲
▲
说一说
找特征
下列多项式能转化成( )2-( )2的形式吗?如果能,请将其转化成( )2-( )2的形式。
(1)
m2
-81
(2)
1
-16b2
(3)
4m2+9
(4)
a2x2
-25y
2
(5)
-x2
-25y2
=
m2
-92
=
12-(4b)2
不能转化为平方差形式
=
(ax)2
-(5y)2
不能转化为平方差形式
试一试
写一写
例1.分解因式:
先确定a和b
范例学习
解:原式
解:原式
1.判断正误:
a2和b2的符号相反
落实基础
(
)
(
)
(
)
(
)
√
×
×
×
2.分解因式:
分解因式需“彻底”!
把括号看作一个整体
能力提升
例2.分解因式:
解:原式
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
结论:
公式中的a、b无论表示数、单项式、还是多项式,只要被分解的多项式能转化成平方差的形式,就能用平方差公式因式分解。
解:原式
方法:
先考虑能否用提取公因式法,再考虑能否用平方差公式分解因式。
解:原式
结论:
分解因式的一般步骤:一提二套
多项式的因式分解要分解到不能再分解为止。
巩固练习
1.把下列各式分解因式:
2.简便计算:
利用因式分解计算
例3.如图,在一块长为a的正方形纸片的四角,各剪去一个边长
为b的正方形.用a
与b表示剩余部分的面积,并求当a=3.6,
b=0.8时的面积.
联系拓广
解:a2-4b2
=(a+2b)(a-2b)cm2
当a=3.6,b=0.8时,
原式=(3.6+2×0.8)
(3.6-2×0.8)
=5.2×2
=10.4cm2
如图,大小两圆的圆心相同,已知它们的半径分别是R
cm和r
cm,求它们所围成的环形的面积。如果R=8.45cm,r=3.45cm呢?
问题解决
解:
R2-
r2
=
(R+r)(R-r)cm2
当R=8.45,r=3.45时,
原式=(8.45+3.45)
×(8.45-3.45)
×3.14
=186.83cm2
自主小结
从今天的课程中,你学到了哪些知识?
掌握了哪些方法?
(1)有公因式(包括负号)则先提取公因式;
(2)整式乘法的平方差公式与因式分解的平方差公式是互逆关系;
(3)平方差公式中的a与b既可以是单项式,又可以是多项式;
作业
完成课本习题
拓展作业:
你能尝试运用今天所学的知识解决下面的问题吗
你知道992-1能否被100整除吗?
如图,在边长为6.8cm正方形钢板上,挖去4个边长为1.6cm的小正方形,求剩余部分的面积。
再攀高峰
第四章
因式分解
3
公式法(二)
一、确定公因式的方法:
提公因式法(复习)
1、公因式的系数是多项式各项__________________;
2、字母取多项式各项中都含有的____________;
3、相同字母的指数取各项中最小的一个,即_________.
系数的最大公约数
相同的字母
最低次幂
二、提公因式法分解因式步骤
(两步):
第一步,找出公因式;
第二步,提公因式,(即用多项式除
以公因式).
公因式
是多项式形式,怎样运用提公因式法分解因式?
想一想
在下列各式等号右边的括号前填入“+”或“-”号,使等式成立:
(a-b)
=___(b-a);
(2)
(a-b)2
=___(b-a)2;
(3)
(a-b)3
=___(b-a)3;
(4)
(a-b)4
=___(b-a)4;
(5)
(a+b)5
=___(b+a)5;
(6)
(a+b)6
=___(b+a)6.
+
-
-
+
+
+
(7)
(a+b)
=___(-b-a);
-
(8)
(a+b)2
=___(-a-b)2.
+
做一做p97
填空
由此可知规律:
(1)a-b
与
-a+b
互为相反数.
(a-b)n
=
(b-a)n
(n是偶数)
(a-b)n
=
-(b-a)n
(n是奇数)
(2)
a+b与b+a
互为相同数,
(a+b)n
=
(b+a)n
(n是整数)
a+b
与
-a-b
互为相反数.
(-a-b)n
=
(a+b)n
(n是偶数)
(-a-b)n
=
-(a+b)n
(n是奇数)
练习一
1.在下列各式右边括号前添上适当的符号,使左边与右边相等.
(1)
a+2
=
___(2+a)
(2)
-x+2y
=
___(2y-x)
(3)
(m-a)2
=
___(a-m)2
(4)
(a-b)3
=
___(-a+b)3
(5)
(x+y)(x-2y)=
___(y+x)(2y-x)
+
+
+
-
-
2.判断下列各式是否正确
(1)
(y-x)2
=
-(x-y)2
(2)
(3+2x)3
=
-(2x+3)3
(3)
a-2b
=
-(-2b+a)
(4)
-a+b
=
-(a+b)
(5)
(a-b)(x-2y)
=
(b-a)(2y-x)
否
否
否
否
对
例1.把
a(x-3)+2b(x-3)
分解因式.
解:
a(x-3)+2b(x-3)
=(x-3)(a+2b)
分析:多项式可看成
a(x-3)
与
2b(x-3)
两项。
公因式为x-3
例题解析
例2.
把a(x-y)+b(y-x)分解因式.
解:
a(x-y)+b(y-x)
=a(x-y)-b(x-y)
=(x-y)(a-b)
分析:多项式可看成a(x-y)与+b(y-x)两项。其中X-y与y-x互为相反数,可将+b(y-x)变为-b(x-y),则a(x-y)与-b(x-y)
公因式为
x-y
例3.
把6(m-n)3-12(n-m)2分解因式.
解:6(m-n)3-12(n-m)2
=
6(m-n)3-12(m-n)2
=
6(m-n)2(m-n-2)
分析:其中(m-n)与(n-m)互为相反数.可将-12(n-m)
2变为-12(m-n)2,则6(m-n)3与-12(m-n)2
公因式为6(m-n)2
例4.把6(x+y)(y-x)2-9(x-y)3分解因式.
解:
6(x+y)(y-x)2-
9(x-y)3
=
6(x+y)(x-y)2-
9(x-y)3
=
3(x-y)2[2(x+y)-3(x-y)]
=
3(x-y)2(2x+2y-3x+3y)
=
3(x-y)2(-x+5y)
=3(x-y)2(5y-x)
(2)
5x(a-b)2+10y(b-a)2
)
3
(
2
3
)
(
12
)
(
6
m
n
n
m
-
-
-
)
1
(
(
(
)
x
y
b
-
-
)
y
x
a
-
分解因式:
(4)
a(a+b)(a-b)-a(a+b)2
(5)
mn(m+n)-m(n+m)2
(6)
2(a-3)2-a+3
(7)
a(x-a)+b(a-x)-c(x-a)
练习二
课堂小结
两个只有符号不同的多项式是否有关系,有如下判断方法:
(1)当相同字母前的符号相同时,
则两个多项式相等.
如:
a-b
和
-b+a
即
a-b
=
-b+a
(2)当相同字母前的符号均相反时,
则两个多项式互为相反数.
如:
a-b
和
b-a
即
a-b
=
-(a-b)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
