2.2.3独立重复试验与二项分布(共37张PPT)
文档属性
| 名称 | 2.2.3独立重复试验与二项分布(共37张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-23 00:00:00 | ||
图片预览










文档简介
(共37张PPT)
2.2.2独立重复试验与 二项分布
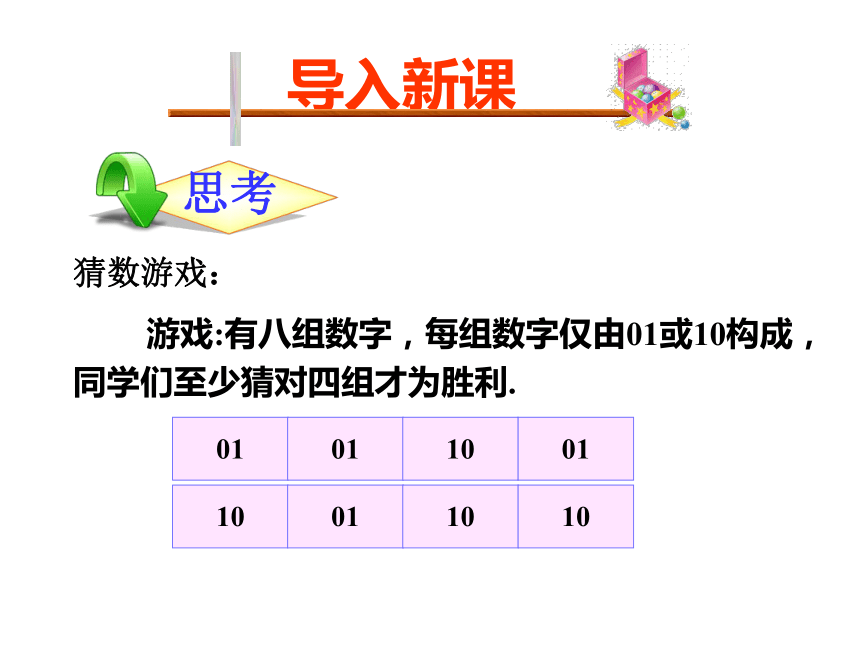
猜数游戏:
游戏:有八组数字,每组数字仅由01或10构成,同学们至少猜对四组才为胜利.
01
01
10
01
10
01
10
10
问题1: 前一次猜测的结果是否影响后一次的猜测?也就是每次猜测是否相互独立?
问题2: 游戏对双方是否公平?能否从概率角度解释?
独立
公平
(1) 求“重复抛一枚硬币 5 次,其有3次正面向上” 的概率.
(2) 求“重复掷一粒骰子3次,其中有2次出现 1 点的概率.
归纳两道题的相同点与不同点!
各次试验的结果不会受其它次试验影响.
相同点 不同点
1.重复做同一件事 “硬币”与“骰子”
“5”与“3”
…… ……
2.前提条件相同
3.都有两个对立的结果
1.独立重复试验
一般地,在相同条件下重复做的n次试验称为n次独立重复试验(independent and repeated trials).
在n次独立重复试验中,“在相同的条件下”等价于各次试验的结果不会受其他试验结果的影响.
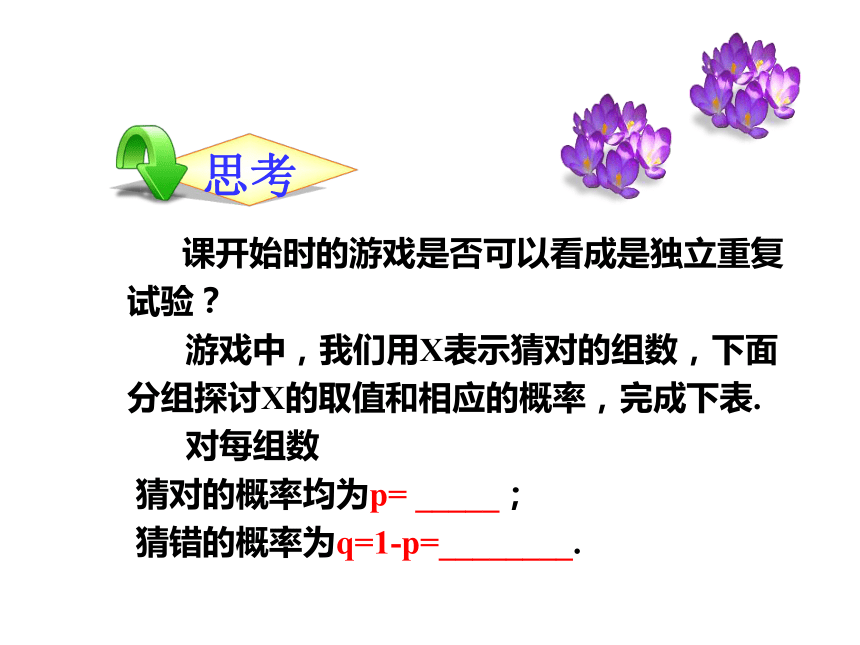
课开始时的游戏是否可以看成是独立重复试验?
游戏中,我们用X表示猜对的组数,下面分组探讨X的取值和相应的概率,完成下表.
对每组数
猜对的概率均为p= _____;
猜错的概率为q=1-p=________.
设AK表示“第K次猜对”的事件;B表示“共猜对K次”的事件(K=1,2,3…8)
猜对组数X 0 1 2 … k … 8
事件情况
概率计算
公式猜想
2.二项分布
在n次独立重复试验中,设事件A发生的次数为X ,在每次试验中事件A发生的概率为p,那么在n次独立重复试验中,事件A恰好发生k 次的概率为
则称随机变量X服从二项分布,
记作 X~B(n,p),也叫Bernolli分布.
实力相等的甲、乙两队参加乒乓球团体比赛,规定5局3胜制(即5局内谁先赢3局就算胜出并停止比赛).
(1)试分别求甲打完3局、4局、5局才能取胜的概率;
(2)按比赛规则甲获胜的概率.
解?:
甲、乙两队实力相等,所以每局比赛甲获胜的概率为0.5,乙获胜的概率为0.5.
记A事件=“甲打完3局才能取胜”,
记B事件=“甲打完4局才能取胜”,
记C事件=“甲打完5局才能取胜”.
①甲打完3局取胜,相当于进行3次独立重复试验,且每局比赛甲均取胜.
∴甲打完3局取胜的概率为
②甲打完4局才能取胜,相当于进行4次独立重复试验,且甲第4局比赛取胜,前3局为2胜1负
∴甲打完4局才能取胜的概率为
③甲打完5局才能取胜,相当于进行5次独立重复试验,且甲第5局比赛取胜,前4局恰好2胜2负
∴甲打完5局才能取胜的概率为
(2)事件D =“按比赛规则甲获胜”,则 D=A+B+C,
又因为事件A 、B 、C 彼此互斥,
故
答:按比赛规则甲获胜的概率为0.5 .
某气象站天气预报的准确率为80% ,计算(结果保留两个有效数字):
(1)5次预报中恰有4次准确的概率;
(2)5次预报中至少有4次准确的概率.
解:
(1)记“预报1次,结果准确”为事件A .预报5次相当于5次独立重复试验,根据 独立重复试验中某事件恰好发生 的概率计算公式,5次预报中恰有4次准确的概率
答:5次预报中恰有4次准确的概率约为0.41.
(2)5次预报中至少有4次准确的概率,就是5次预报中恰有4次准确的概率与5次预报都准确的概率的和,即
答:5次预报中至少有4次准确的概率约为0.74.
某人对一目标进行射击,每次命中率都是0.25,若使至少命中1次的概率不小于0.75,至少应射击几次?
解:设要使至少命中1次的概率不小于0.75,应射击n 次
记事件A =“射击一次,击中目标”,则P(A)=0.25.
∵射击n 次相当于n 次独立重复试验,
∴事件至少发生1次的概率为P=1-Pn(0)=1-0.75n.
由题意,令1-0.75n ≥0.75,
∴0.75n≤0.25 ,
∴ ,
∴n 至少取5.
答:要使至少命中1次的概率不小于0.75,至少应射击5次 .
1.独立重复试验的理解
(1)理解独立重复试验,试验的结果只有两种,要么发生,要么不发生.
(2)若在独立重复试验中,发生的概率为P,则不发生的概率为1-P.
(3)若在n次独立重复试验中,事件A发生的次数为X,每一次发生的概率为P,在独立重复试验中,事件A发生k次的概率公式为
P(X=k)=Cnkpk(1-p)n-k
2.能力总结
① 分清事件类型;
② 转化复杂问题为基本的互斥事件与相互独立事件.
3.思想、方法
① 分类讨论、归纳与演绎的方法;
② 辩证思想.
1. (2017年高考题)某厂生产电子元件,其产品的次品率为5%.现从一批产品中任意地连续取出2件,写出其中次品数ξ的概率分布.
解:
依题意,随机变量ξ~B(2,5%).所以,
P(ξ=0)=C20(95%)2=0.9025;
P(ξ=1)=C21(95%)(5%)=0.095;
P(ξ=2)=C22(5%)2=0.0025.
因此,次品数ξ的概率分布是
ξ 0 1 2
P 0.9025 0.095 0.0025
1.填空
(1)某人考试,共有5题,解对4题为及格,若他解一道题正确率为0.6,则他及格概率为_____.
分析:
该题服从二项分布X~B(5,0.6)求的是当X=4时的概率.
(2)若某射手每次射击击中目标的概率是0.9,每次射击的结果相互独立,那么在他连续4次的射击中,第一次未击中目标,后三次都击中目标的概率是_____________.
0.93*0.1
分析:
仔细看题可知,该题并非二项分布.
(2)随机变量X~B ( 3, 0.6 ) ,P ( X=1 ) =( )
A. 0.192 B. 0.288 C. 0.648 D. 0.254
(1)将一枚硬币连续抛掷5次,则正面向上的次数X的分布为( )
A. X~B ( 5,0.5 ) B. X~B (0.5,5 )
C. X~B ( 2,0.5 ) D. X~B ( 5,1 )
2.选择
√
√
3.解答题
(1)十层电梯从低层到顶层停不少于3次的概率是多少?停几次概率最大?
解:
依题意,从低层到顶层停不少于3次,应包括停3次,停4次,停5次,……,直到停9次.
∴从低层到顶层停不少于3次的概率:
设从低层到顶层停k次,则其概率为
当k=4或k=5时,C9k最大,即C9k(0.5)9最大
答:从低层到顶层停不少于3次的概率为233/256,停4次或5次概率最大.
(2)一批玉米种子,其发芽率是0.8.
①问每穴至少种几粒,才能保证每穴至少有一粒发芽的概率大于98%?
②若每穴种3粒,求恰好两粒发芽的概率( ).
解:
记事件A=“种一粒种子,发芽”,则
P(A)=0.8,P(A)=1-0.8=0.2,
①设每穴至少种n粒,才能保证每穴至少有一粒发芽的概率大于98% .
∵每穴种n粒相当于n次独立重复试验,记事件B=“每穴至少有一粒发芽”,则
∴
由题意,令P(B)>98%,所以0.2n<0.02,两边取常用对数得,
.即 ,
∴ ,且 ,所以取n≥3 .
答:每穴至少种3粒,才能保证每穴至少有一粒发芽的概率大于98% .
② ∵每穴种3粒相当于3次独立重复试验,
∴每穴种3粒,恰好两粒发芽的概率为
答:每穴种3粒,恰好两粒发芽的概率为0.384 .
(3)某车间的5台机床在1小时内需要工人照管的概率都是1/4,求1小时内5台机床中至少2台需要工人照管的概率是多少?(结果保留两个有效数字)
解:
记事件A=“1小时内,1台机器需要人照管”,1小时内5台机器需要照管相当于5次独立重复试验
1小时内5台机床中没有1台需要工人照管的概率
1小时内5台机床中恰有1台需要工人照管的概率为
所以1小时内5台机床中至少2台需要工人照管的概率为
答:1小时内5台机床中至少2台需要工人照管的概率约为0.37.
1. 用A表示抽到的这件产品为合格品,Ai表示这件产品在第i道工序中质量合格,i=1,2,3,4,5.则A=A1∩A2∩A3∩A4∩A5,
P(A1)=0.96, P(A2)=0.99, P(A3)=0.98, P(A4)=0.97, P(A5)=0.96,且A1,A2,A3,A4,A5相互独立.所以
P(A)=P(A1)P(A2)P(A3)P(A4)P(A5)
=0.96×0.99×0.98×0.97×0.96
≈0.867.
2.将一枚硬币连续抛掷5次,正面向上的次数X服从二项分布,其分布列为
P(X=k)=C5k(1/2)5,k=0,1,2,3,4,5.
用表格的形式表示如下:
X 0 1 2 3 4 5
P 1/25 5/25 10/25 10/25 5/25 1/25
P(B)=P(A1)P(A2)P(A3)P(A4)
=(1-0.9) ×0.9×0.9×0.9
=0.0729.
3. 用事件B表示仅第1次未击中目标,事件Ai表示该射手第i次设计击中目标,i=1,2,3,4,则B=A1A2A3A4。因为4次射击可以看成4次独立重复试验,所以可以利用独立事件公式计算B发生的概率:
4.例1 某同学投篮命中率为0.6,他在6次投篮中命中的次数X是一个随机变量,X~B(6,0.6).
例2 在一次考试中有10道单选题,某同学一道题都不会,随机的选择答案,这10道单选题中答对的个数X是一个随机变量,X~B(10,0.25).
2.2.2独立重复试验与 二项分布
猜数游戏:
游戏:有八组数字,每组数字仅由01或10构成,同学们至少猜对四组才为胜利.
01
01
10
01
10
01
10
10
问题1: 前一次猜测的结果是否影响后一次的猜测?也就是每次猜测是否相互独立?
问题2: 游戏对双方是否公平?能否从概率角度解释?
独立
公平
(1) 求“重复抛一枚硬币 5 次,其有3次正面向上” 的概率.
(2) 求“重复掷一粒骰子3次,其中有2次出现 1 点的概率.
归纳两道题的相同点与不同点!
各次试验的结果不会受其它次试验影响.
相同点 不同点
1.重复做同一件事 “硬币”与“骰子”
“5”与“3”
…… ……
2.前提条件相同
3.都有两个对立的结果
1.独立重复试验
一般地,在相同条件下重复做的n次试验称为n次独立重复试验(independent and repeated trials).
在n次独立重复试验中,“在相同的条件下”等价于各次试验的结果不会受其他试验结果的影响.
课开始时的游戏是否可以看成是独立重复试验?
游戏中,我们用X表示猜对的组数,下面分组探讨X的取值和相应的概率,完成下表.
对每组数
猜对的概率均为p= _____;
猜错的概率为q=1-p=________.
设AK表示“第K次猜对”的事件;B表示“共猜对K次”的事件(K=1,2,3…8)
猜对组数X 0 1 2 … k … 8
事件情况
概率计算
公式猜想
2.二项分布
在n次独立重复试验中,设事件A发生的次数为X ,在每次试验中事件A发生的概率为p,那么在n次独立重复试验中,事件A恰好发生k 次的概率为
则称随机变量X服从二项分布,
记作 X~B(n,p),也叫Bernolli分布.
实力相等的甲、乙两队参加乒乓球团体比赛,规定5局3胜制(即5局内谁先赢3局就算胜出并停止比赛).
(1)试分别求甲打完3局、4局、5局才能取胜的概率;
(2)按比赛规则甲获胜的概率.
解?:
甲、乙两队实力相等,所以每局比赛甲获胜的概率为0.5,乙获胜的概率为0.5.
记A事件=“甲打完3局才能取胜”,
记B事件=“甲打完4局才能取胜”,
记C事件=“甲打完5局才能取胜”.
①甲打完3局取胜,相当于进行3次独立重复试验,且每局比赛甲均取胜.
∴甲打完3局取胜的概率为
②甲打完4局才能取胜,相当于进行4次独立重复试验,且甲第4局比赛取胜,前3局为2胜1负
∴甲打完4局才能取胜的概率为
③甲打完5局才能取胜,相当于进行5次独立重复试验,且甲第5局比赛取胜,前4局恰好2胜2负
∴甲打完5局才能取胜的概率为
(2)事件D =“按比赛规则甲获胜”,则 D=A+B+C,
又因为事件A 、B 、C 彼此互斥,
故
答:按比赛规则甲获胜的概率为0.5 .
某气象站天气预报的准确率为80% ,计算(结果保留两个有效数字):
(1)5次预报中恰有4次准确的概率;
(2)5次预报中至少有4次准确的概率.
解:
(1)记“预报1次,结果准确”为事件A .预报5次相当于5次独立重复试验,根据 独立重复试验中某事件恰好发生 的概率计算公式,5次预报中恰有4次准确的概率
答:5次预报中恰有4次准确的概率约为0.41.
(2)5次预报中至少有4次准确的概率,就是5次预报中恰有4次准确的概率与5次预报都准确的概率的和,即
答:5次预报中至少有4次准确的概率约为0.74.
某人对一目标进行射击,每次命中率都是0.25,若使至少命中1次的概率不小于0.75,至少应射击几次?
解:设要使至少命中1次的概率不小于0.75,应射击n 次
记事件A =“射击一次,击中目标”,则P(A)=0.25.
∵射击n 次相当于n 次独立重复试验,
∴事件至少发生1次的概率为P=1-Pn(0)=1-0.75n.
由题意,令1-0.75n ≥0.75,
∴0.75n≤0.25 ,
∴ ,
∴n 至少取5.
答:要使至少命中1次的概率不小于0.75,至少应射击5次 .
1.独立重复试验的理解
(1)理解独立重复试验,试验的结果只有两种,要么发生,要么不发生.
(2)若在独立重复试验中,发生的概率为P,则不发生的概率为1-P.
(3)若在n次独立重复试验中,事件A发生的次数为X,每一次发生的概率为P,在独立重复试验中,事件A发生k次的概率公式为
P(X=k)=Cnkpk(1-p)n-k
2.能力总结
① 分清事件类型;
② 转化复杂问题为基本的互斥事件与相互独立事件.
3.思想、方法
① 分类讨论、归纳与演绎的方法;
② 辩证思想.
1. (2017年高考题)某厂生产电子元件,其产品的次品率为5%.现从一批产品中任意地连续取出2件,写出其中次品数ξ的概率分布.
解:
依题意,随机变量ξ~B(2,5%).所以,
P(ξ=0)=C20(95%)2=0.9025;
P(ξ=1)=C21(95%)(5%)=0.095;
P(ξ=2)=C22(5%)2=0.0025.
因此,次品数ξ的概率分布是
ξ 0 1 2
P 0.9025 0.095 0.0025
1.填空
(1)某人考试,共有5题,解对4题为及格,若他解一道题正确率为0.6,则他及格概率为_____.
分析:
该题服从二项分布X~B(5,0.6)求的是当X=4时的概率.
(2)若某射手每次射击击中目标的概率是0.9,每次射击的结果相互独立,那么在他连续4次的射击中,第一次未击中目标,后三次都击中目标的概率是_____________.
0.93*0.1
分析:
仔细看题可知,该题并非二项分布.
(2)随机变量X~B ( 3, 0.6 ) ,P ( X=1 ) =( )
A. 0.192 B. 0.288 C. 0.648 D. 0.254
(1)将一枚硬币连续抛掷5次,则正面向上的次数X的分布为( )
A. X~B ( 5,0.5 ) B. X~B (0.5,5 )
C. X~B ( 2,0.5 ) D. X~B ( 5,1 )
2.选择
√
√
3.解答题
(1)十层电梯从低层到顶层停不少于3次的概率是多少?停几次概率最大?
解:
依题意,从低层到顶层停不少于3次,应包括停3次,停4次,停5次,……,直到停9次.
∴从低层到顶层停不少于3次的概率:
设从低层到顶层停k次,则其概率为
当k=4或k=5时,C9k最大,即C9k(0.5)9最大
答:从低层到顶层停不少于3次的概率为233/256,停4次或5次概率最大.
(2)一批玉米种子,其发芽率是0.8.
①问每穴至少种几粒,才能保证每穴至少有一粒发芽的概率大于98%?
②若每穴种3粒,求恰好两粒发芽的概率( ).
解:
记事件A=“种一粒种子,发芽”,则
P(A)=0.8,P(A)=1-0.8=0.2,
①设每穴至少种n粒,才能保证每穴至少有一粒发芽的概率大于98% .
∵每穴种n粒相当于n次独立重复试验,记事件B=“每穴至少有一粒发芽”,则
∴
由题意,令P(B)>98%,所以0.2n<0.02,两边取常用对数得,
.即 ,
∴ ,且 ,所以取n≥3 .
答:每穴至少种3粒,才能保证每穴至少有一粒发芽的概率大于98% .
② ∵每穴种3粒相当于3次独立重复试验,
∴每穴种3粒,恰好两粒发芽的概率为
答:每穴种3粒,恰好两粒发芽的概率为0.384 .
(3)某车间的5台机床在1小时内需要工人照管的概率都是1/4,求1小时内5台机床中至少2台需要工人照管的概率是多少?(结果保留两个有效数字)
解:
记事件A=“1小时内,1台机器需要人照管”,1小时内5台机器需要照管相当于5次独立重复试验
1小时内5台机床中没有1台需要工人照管的概率
1小时内5台机床中恰有1台需要工人照管的概率为
所以1小时内5台机床中至少2台需要工人照管的概率为
答:1小时内5台机床中至少2台需要工人照管的概率约为0.37.
1. 用A表示抽到的这件产品为合格品,Ai表示这件产品在第i道工序中质量合格,i=1,2,3,4,5.则A=A1∩A2∩A3∩A4∩A5,
P(A1)=0.96, P(A2)=0.99, P(A3)=0.98, P(A4)=0.97, P(A5)=0.96,且A1,A2,A3,A4,A5相互独立.所以
P(A)=P(A1)P(A2)P(A3)P(A4)P(A5)
=0.96×0.99×0.98×0.97×0.96
≈0.867.
2.将一枚硬币连续抛掷5次,正面向上的次数X服从二项分布,其分布列为
P(X=k)=C5k(1/2)5,k=0,1,2,3,4,5.
用表格的形式表示如下:
X 0 1 2 3 4 5
P 1/25 5/25 10/25 10/25 5/25 1/25
P(B)=P(A1)P(A2)P(A3)P(A4)
=(1-0.9) ×0.9×0.9×0.9
=0.0729.
3. 用事件B表示仅第1次未击中目标,事件Ai表示该射手第i次设计击中目标,i=1,2,3,4,则B=A1A2A3A4。因为4次射击可以看成4次独立重复试验,所以可以利用独立事件公式计算B发生的概率:
4.例1 某同学投篮命中率为0.6,他在6次投篮中命中的次数X是一个随机变量,X~B(6,0.6).
例2 在一次考试中有10道单选题,某同学一道题都不会,随机的选择答案,这10道单选题中答对的个数X是一个随机变量,X~B(10,0.25).
