人教版八年级数学下册18.1.1平行四边形性质课件(26张PPT)
文档属性
| 名称 | 人教版八年级数学下册18.1.1平行四边形性质课件(26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 918.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-24 08:32:58 | ||
图片预览





文档简介
(共27张PPT)
优秀团员主要事迹材料汇报1000字
中国共产主义青年团具有如下特点:1.先进性 2.群众性 3.实践性,是中国共产党领导的先进青年的群众组织,是广大青年在实践中学习中国特色社会主义和共产主义的学校,是中国共产党的助手和后备军。中国共产主义青年团坚决拥护中国共产党的纲领,以马克思列宁主义、毛泽东思想、邓小平理论、“三个代表”重要思想、科学发展观为行动指南,深入贯彻落实科学发展观,解放思想,实事求是,与时俱进,团结全国各族青年,为把我国建设成为富强、民主、文明、和谐的社会主义现代化国家,为最终实现共产主义而奋斗。
的,供大家参考。
我是实验中学初42班的一名共青团员。入团后,我深刻地认识到:共青团作为共产党的后备主力军,有着不可替代的作用。中国共产主义青年团是青年的先进组织,要成为一名优秀的共青团员,我们必须严格执行团员的章程和组织原则,在各方面都严格要求自己,通过不断地学习来完善自己,为青年带好头,处处领先,争当青年团员的模范。作为共青团中的一员,我感到非常自豪。在本学期,我申请争当优秀共青团员,请上级领导对我的表现进行审查。
在思想上,我始终坚持正确的人生观和价值观;坚持马
克思列宁主
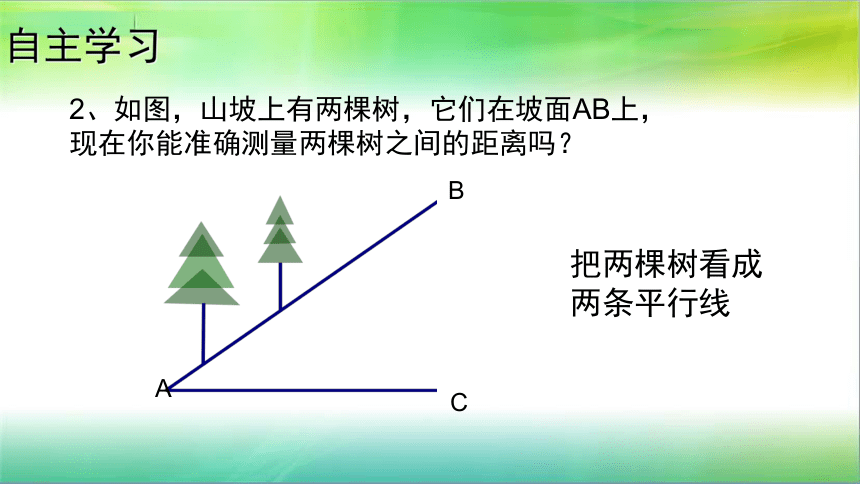
情境创设
山坡上有两棵树,现在想要测量这两棵树之间的距离,如图,BAC是山坡的横截面,两棵树在坡面AB上,你能测量出两棵树距离吗?
A
B
C
人教版数学八年级下册
平行四边形的性质——
平行线间的距离及等面积问题
会运用平行线间距离处处相等解决一般三角形的面积问题;
在图形的变换中体会数学中的转化思想.
1
2
3
理解并掌握平行线间距离处处相等的性质;
学习目标
自主学习
1、知识准备:
(2)点到直线的距离是指过这个点所作直线的垂线段的 。
(3)两平行线间的距离是指 ,如图,m∥n,则直线m与直线n之间的距离是 。
(1)三角形的面积公式是 。
底×高÷2
长度
其中一条直线上任意一点到另一条直线的距离
线段AB的长度
(4)平行四边形中,对边 .同时,每一组对边都是另一组对边之间的平行线段,因此上述结论可以这样说:平行线之间的平行线段相等.
平行且相等
自主学习
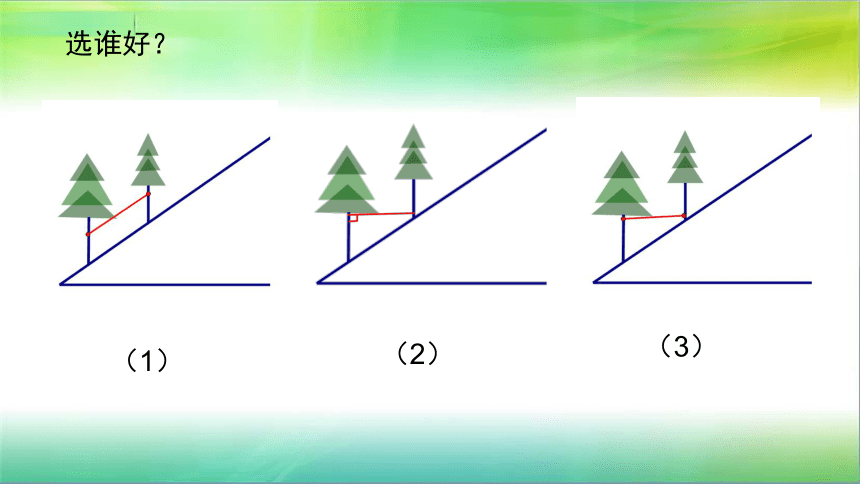
2、如图,山坡上有两棵树,它们在坡面AB上,现在你能准确测量两棵树之间的距离吗?
A
B
C
把两棵树看成两条平行线
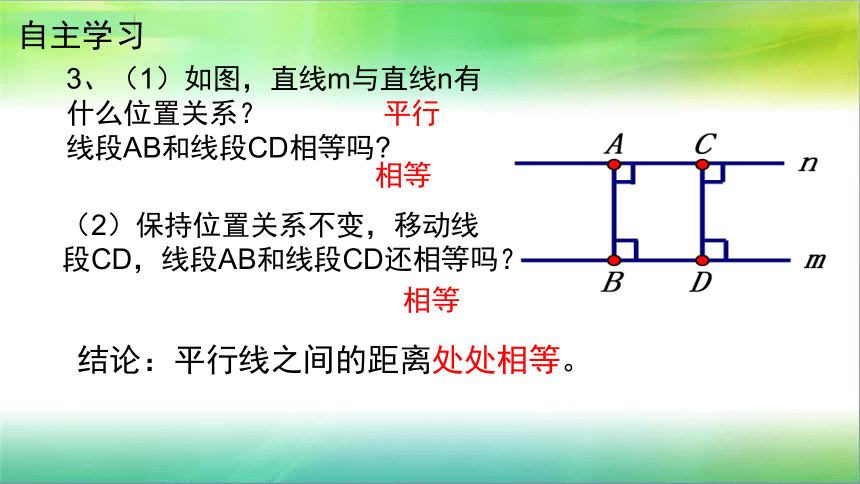
(1)
(2)
(3)
选谁好?
自主学习
结论:平行线之间的距离处处相等。
3、(1)如图,直线m与直线n有什么位置关系?
线段AB和线段CD相等吗?
(2)保持位置关系不变,移动线段CD,线段AB和线段CD还相等吗?
平行
相等
相等
自主学习
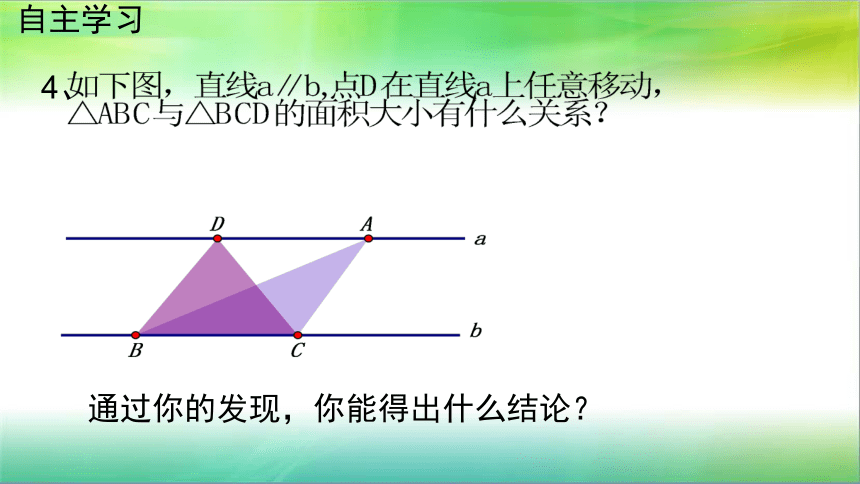
通过你的发现,你能得出什么结论?
4、
总结一:两个三角形面积相等的情况:
①等底等高的两个三角形面积相等;
②底在同一直线上并且相等,该底所对的角的顶点是同一个点或者在与底平行的直线上,这两个三角形面积相等;
根据: 平行线间的距离处处相等,
总结二:可以将一些不便求解的三角形的面积问题转化为方便求解的三角形的面积问题.
例1、如图,四边形ABCD中,AD∥BC,则图中面积相等的三角形有几对?请你试着找出来。
答案:
S△ABD=S△ACD
S△ABC=S△BCD
S△ABO=S△CDO
精讲点拨
思考:若四边形ABCD是平行四边形,面积相等的三角形又有几对?
例2 如图,有一块草坪,被一条小路隔开,现在要把这条小路改成直路,并且还要保证小路两旁的草坪的面积不变,你有解决方案吗?
精讲点拨
草坪
草坪
解决方案:
方案一
方案二
请你参考小华的学习经验画图(保留画图痕迹):
(1)如图,已知△ABC,画出一个等腰△DBC,
使其面积与△ABC面积相等;
(2)如图,已知△ABC,画出两个Rt△DBC,
使其面积与△ABC面积相等(要求:所画的两个三角形不全等);
小试牛刀
精讲点拨
将一般三角形的面积问题转化为方便求解的三角形问题:
首先要将三角形的某一方便求解的边作为底边,过顶点找出这条底边的平行线,
根据平行线之间的距离处处相等,在平行线上移动顶点,找出我们可以求解或者满足条件的三角形。
1号
2号
3号
4号
抽奖啦!
1、(2015?六盘水第20题)如图,已知,l1∥l2,C1在l1上,并且C1A⊥l2,A为垂足,C2,C3是l1上任意两点,点B在l2上.设△ABC1的面积为S1,△ABC2的面积为S2,△ABC3的面积为S3,小颖认为S1=S2=S3,请帮小颖说明理由.
当堂检测
2、如图,点E、F分别是□ ABCD的边AD、BC上的点,AF和BE交于点P,DF和CE交于点Q,△ABP的面积等于15,△CDQ的面积等于20,则图中阴影部分的面积= 。
3、四边形ABCD与CEFG是菱形,其中四边形ABCD的面积是8.
求△BDF的面积.
小结:请你谈谈今天的收获?
一种思想
一种方法
两个知识点
1、平行线间的距离处处相等
2、等底等高的三角形面积相等
小结:请你谈谈今天的收获?
一种思想:转化
将不便求解面积的三角形
便于求解面积的三角形
将一般三角形的面积问题转化为方便求解的三角形问题:
首先要将三角形的某一方便求解的边作为底边,过顶点找出这条底边的平行线,
根据平行线之间的距离处处相等,在平行线上移动顶点,找出我们可以求解或者满足条件的三角形。
方法:
小结
1、(1)如图△ABC,点D为BC边中点,则S△ABD与S△ACD的关系怎样?
(2)如图△ABC,点D为BC边上一点,且BD:BC=2:1,则S△ABD与S△ACD的关系怎样?
作业:
结论:若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
2、如图2,O为□ABCD的对角线交点,E为AB的中点,DE交AC于点F,若□ABCD的面积为12,则△DOE的面积为( )
A、1 B、1.5 C、2 D、2.25
作业:
如图:五边形ABCDE,过点A作一条直线,将五边形平分成面积相等的两部分。请你做出你的设计方法,并说明理由。
拓展提升:
答案
路漫漫其修远兮,吾将上下而求索!
——屈原
恭喜你,你中奖啦!
优秀团员主要事迹材料汇报1000字
中国共产主义青年团具有如下特点:1.先进性 2.群众性 3.实践性,是中国共产党领导的先进青年的群众组织,是广大青年在实践中学习中国特色社会主义和共产主义的学校,是中国共产党的助手和后备军。中国共产主义青年团坚决拥护中国共产党的纲领,以马克思列宁主义、毛泽东思想、邓小平理论、“三个代表”重要思想、科学发展观为行动指南,深入贯彻落实科学发展观,解放思想,实事求是,与时俱进,团结全国各族青年,为把我国建设成为富强、民主、文明、和谐的社会主义现代化国家,为最终实现共产主义而奋斗。
的,供大家参考。
我是实验中学初42班的一名共青团员。入团后,我深刻地认识到:共青团作为共产党的后备主力军,有着不可替代的作用。中国共产主义青年团是青年的先进组织,要成为一名优秀的共青团员,我们必须严格执行团员的章程和组织原则,在各方面都严格要求自己,通过不断地学习来完善自己,为青年带好头,处处领先,争当青年团员的模范。作为共青团中的一员,我感到非常自豪。在本学期,我申请争当优秀共青团员,请上级领导对我的表现进行审查。
在思想上,我始终坚持正确的人生观和价值观;坚持马
克思列宁主
情境创设
山坡上有两棵树,现在想要测量这两棵树之间的距离,如图,BAC是山坡的横截面,两棵树在坡面AB上,你能测量出两棵树距离吗?
A
B
C
人教版数学八年级下册
平行四边形的性质——
平行线间的距离及等面积问题
会运用平行线间距离处处相等解决一般三角形的面积问题;
在图形的变换中体会数学中的转化思想.
1
2
3
理解并掌握平行线间距离处处相等的性质;
学习目标
自主学习
1、知识准备:
(2)点到直线的距离是指过这个点所作直线的垂线段的 。
(3)两平行线间的距离是指 ,如图,m∥n,则直线m与直线n之间的距离是 。
(1)三角形的面积公式是 。
底×高÷2
长度
其中一条直线上任意一点到另一条直线的距离
线段AB的长度
(4)平行四边形中,对边 .同时,每一组对边都是另一组对边之间的平行线段,因此上述结论可以这样说:平行线之间的平行线段相等.
平行且相等
自主学习
2、如图,山坡上有两棵树,它们在坡面AB上,现在你能准确测量两棵树之间的距离吗?
A
B
C
把两棵树看成两条平行线
(1)
(2)
(3)
选谁好?
自主学习
结论:平行线之间的距离处处相等。
3、(1)如图,直线m与直线n有什么位置关系?
线段AB和线段CD相等吗?
(2)保持位置关系不变,移动线段CD,线段AB和线段CD还相等吗?
平行
相等
相等
自主学习
通过你的发现,你能得出什么结论?
4、
总结一:两个三角形面积相等的情况:
①等底等高的两个三角形面积相等;
②底在同一直线上并且相等,该底所对的角的顶点是同一个点或者在与底平行的直线上,这两个三角形面积相等;
根据: 平行线间的距离处处相等,
总结二:可以将一些不便求解的三角形的面积问题转化为方便求解的三角形的面积问题.
例1、如图,四边形ABCD中,AD∥BC,则图中面积相等的三角形有几对?请你试着找出来。
答案:
S△ABD=S△ACD
S△ABC=S△BCD
S△ABO=S△CDO
精讲点拨
思考:若四边形ABCD是平行四边形,面积相等的三角形又有几对?
例2 如图,有一块草坪,被一条小路隔开,现在要把这条小路改成直路,并且还要保证小路两旁的草坪的面积不变,你有解决方案吗?
精讲点拨
草坪
草坪
解决方案:
方案一
方案二
请你参考小华的学习经验画图(保留画图痕迹):
(1)如图,已知△ABC,画出一个等腰△DBC,
使其面积与△ABC面积相等;
(2)如图,已知△ABC,画出两个Rt△DBC,
使其面积与△ABC面积相等(要求:所画的两个三角形不全等);
小试牛刀
精讲点拨
将一般三角形的面积问题转化为方便求解的三角形问题:
首先要将三角形的某一方便求解的边作为底边,过顶点找出这条底边的平行线,
根据平行线之间的距离处处相等,在平行线上移动顶点,找出我们可以求解或者满足条件的三角形。
1号
2号
3号
4号
抽奖啦!
1、(2015?六盘水第20题)如图,已知,l1∥l2,C1在l1上,并且C1A⊥l2,A为垂足,C2,C3是l1上任意两点,点B在l2上.设△ABC1的面积为S1,△ABC2的面积为S2,△ABC3的面积为S3,小颖认为S1=S2=S3,请帮小颖说明理由.
当堂检测
2、如图,点E、F分别是□ ABCD的边AD、BC上的点,AF和BE交于点P,DF和CE交于点Q,△ABP的面积等于15,△CDQ的面积等于20,则图中阴影部分的面积= 。
3、四边形ABCD与CEFG是菱形,其中四边形ABCD的面积是8.
求△BDF的面积.
小结:请你谈谈今天的收获?
一种思想
一种方法
两个知识点
1、平行线间的距离处处相等
2、等底等高的三角形面积相等
小结:请你谈谈今天的收获?
一种思想:转化
将不便求解面积的三角形
便于求解面积的三角形
将一般三角形的面积问题转化为方便求解的三角形问题:
首先要将三角形的某一方便求解的边作为底边,过顶点找出这条底边的平行线,
根据平行线之间的距离处处相等,在平行线上移动顶点,找出我们可以求解或者满足条件的三角形。
方法:
小结
1、(1)如图△ABC,点D为BC边中点,则S△ABD与S△ACD的关系怎样?
(2)如图△ABC,点D为BC边上一点,且BD:BC=2:1,则S△ABD与S△ACD的关系怎样?
作业:
结论:若两个三角形的高(或底)相等,其中一个三角形的底(或高)是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
2、如图2,O为□ABCD的对角线交点,E为AB的中点,DE交AC于点F,若□ABCD的面积为12,则△DOE的面积为( )
A、1 B、1.5 C、2 D、2.25
作业:
如图:五边形ABCDE,过点A作一条直线,将五边形平分成面积相等的两部分。请你做出你的设计方法,并说明理由。
拓展提升:
答案
路漫漫其修远兮,吾将上下而求索!
——屈原
恭喜你,你中奖啦!
