五年级下册数学课件-3.3第2课时 长方体和正方体的体积(1) 人教版(共18张PPT)
文档属性
| 名称 | 五年级下册数学课件-3.3第2课时 长方体和正方体的体积(1) 人教版(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-24 10:14:19 | ||
图片预览



文档简介
(共18张PPT)
第 2 课时 长方体和正方体的体积(1)
一、情境导入,探索新知
怎样计算长方体的体积呢?
怎样知道一个长方体的体积呢?
二、动手操作,探究长方体的体积计算方法
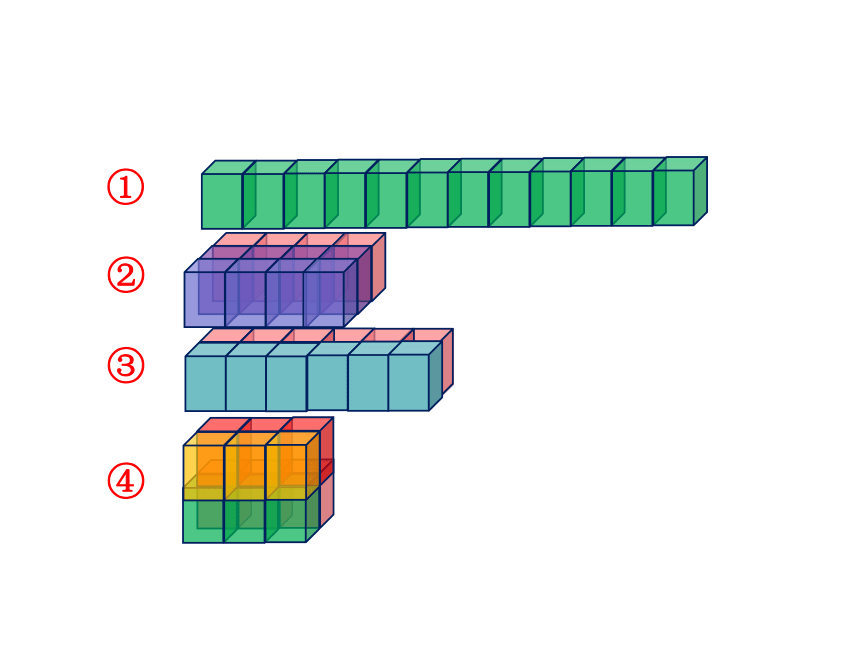
用 12 个棱长为 1 cm 的小正方体拼摆不同形状的长方体,它们的长、宽、高各是多少?体积又是多少呢?
①
②
③
④
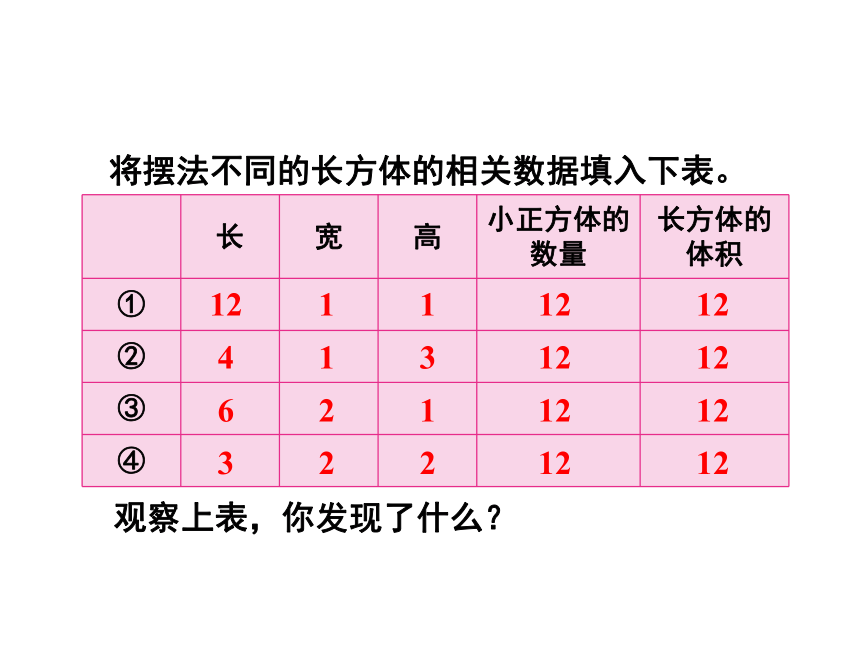
将摆法不同的长方体的相关数据填入下表。
12
1
1
12
12
4
1
3
12
12
6
2
1
12
12
3
2
2
12
12
观察上表,你发现了什么?
长 宽 高 小正方体的数量 长方体的体积
①
②
③
④
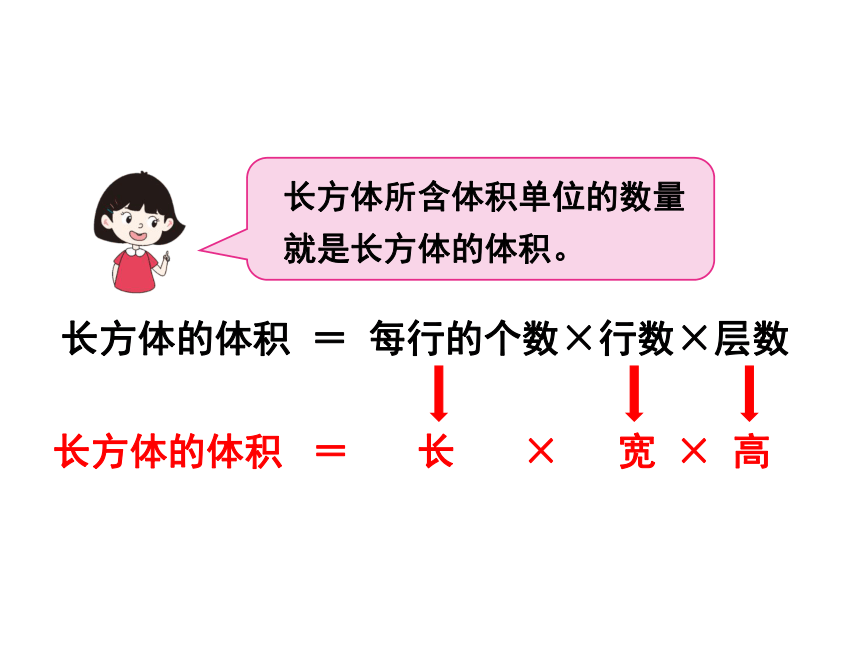
长方体所含体积单位的数量就是长方体的体积。
长方体的体积 = 每行的个数×行数×层数
长 宽 高
长方体的体积 = × ×
如果用字母 V 表示长方体的体积,用 a、b、h 分别表示长方体的长、宽、高。
长方体的体积=长×宽×高
V = abh
正方体的体积可以怎样计算? 与长方体体积的计算有什么相同和不同?
正方体的体积 = 棱长×棱长×棱长
V = a · a · a
V = a3
计算下面图形的体积。
V=abh
=7×3×4
=84(cm3)
V=a3
=63
=6×6×6
=216(dm3)
三、理解应用,巩固提高
自学教科书 P31 内容,并思考以下问题。
★什么叫底面积?
★长方体的底面积怎么求? 正方体呢?
★为什么长方体和正方体的体积公式都可以用“底面积×高”来表示?
★这个公式用字母怎么表示?
四、深化理解,统一公式
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长方体(或正方体)的体积=底面积×高
V = Sh
长方体或正方体底面的面积叫做底面积。
1.一块长方体肥皂的尺寸如下图,它的体积是多少?
V=abh
=15×7×8
=840(cm3)
答:它的体积是840cm3。
五、实践应用,内化知识
2.一根长方体木料,长 5 m,横截面的面积是 0.06 m2。这根木料的体积是多少?
V = Sh
= 0.06×5
= 0.3(m3)
答:这根木料的体积是 0.3 m3。
苹果醋饮料箱:长、宽、高分别是 70 厘米、50 厘米、60 厘米,它的体积是多少?
V = abh
= 70×50×60
= 210000(cm3)
答:它的体积是 210000 cm3。
六、课堂小结
长方体的体积=长×宽×高
V=abh
正方体的体积=棱长×棱长×棱长
V= a3
长方体(或正方体)的体积=底面积×高
V = Sh
一、选一选。 (将正确答案的序号填在括号里)
?备选练习
1. a3 表示( )。
A.a×3 B.a+a+a C.a×a×a
2. 正方体的棱长扩大到原来的 3 倍,它的体积就扩大到原来的( )。
A.3 倍 B.9 倍 C.27 倍
C
C
二、80 本相同的故事书摆成一个长 25 cm、宽16 cm、高 12 cm 的长方体,你能求出每本故事书的体积是多少吗?
25×16×12÷80 = 60(cm3)
第 2 课时 长方体和正方体的体积(1)
一、情境导入,探索新知
怎样计算长方体的体积呢?
怎样知道一个长方体的体积呢?
二、动手操作,探究长方体的体积计算方法
用 12 个棱长为 1 cm 的小正方体拼摆不同形状的长方体,它们的长、宽、高各是多少?体积又是多少呢?
①
②
③
④
将摆法不同的长方体的相关数据填入下表。
12
1
1
12
12
4
1
3
12
12
6
2
1
12
12
3
2
2
12
12
观察上表,你发现了什么?
长 宽 高 小正方体的数量 长方体的体积
①
②
③
④
长方体所含体积单位的数量就是长方体的体积。
长方体的体积 = 每行的个数×行数×层数
长 宽 高
长方体的体积 = × ×
如果用字母 V 表示长方体的体积,用 a、b、h 分别表示长方体的长、宽、高。
长方体的体积=长×宽×高
V = abh
正方体的体积可以怎样计算? 与长方体体积的计算有什么相同和不同?
正方体的体积 = 棱长×棱长×棱长
V = a · a · a
V = a3
计算下面图形的体积。
V=abh
=7×3×4
=84(cm3)
V=a3
=63
=6×6×6
=216(dm3)
三、理解应用,巩固提高
自学教科书 P31 内容,并思考以下问题。
★什么叫底面积?
★长方体的底面积怎么求? 正方体呢?
★为什么长方体和正方体的体积公式都可以用“底面积×高”来表示?
★这个公式用字母怎么表示?
四、深化理解,统一公式
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长方体(或正方体)的体积=底面积×高
V = Sh
长方体或正方体底面的面积叫做底面积。
1.一块长方体肥皂的尺寸如下图,它的体积是多少?
V=abh
=15×7×8
=840(cm3)
答:它的体积是840cm3。
五、实践应用,内化知识
2.一根长方体木料,长 5 m,横截面的面积是 0.06 m2。这根木料的体积是多少?
V = Sh
= 0.06×5
= 0.3(m3)
答:这根木料的体积是 0.3 m3。
苹果醋饮料箱:长、宽、高分别是 70 厘米、50 厘米、60 厘米,它的体积是多少?
V = abh
= 70×50×60
= 210000(cm3)
答:它的体积是 210000 cm3。
六、课堂小结
长方体的体积=长×宽×高
V=abh
正方体的体积=棱长×棱长×棱长
V= a3
长方体(或正方体)的体积=底面积×高
V = Sh
一、选一选。 (将正确答案的序号填在括号里)
?备选练习
1. a3 表示( )。
A.a×3 B.a+a+a C.a×a×a
2. 正方体的棱长扩大到原来的 3 倍,它的体积就扩大到原来的( )。
A.3 倍 B.9 倍 C.27 倍
C
C
二、80 本相同的故事书摆成一个长 25 cm、宽16 cm、高 12 cm 的长方体,你能求出每本故事书的体积是多少吗?
25×16×12÷80 = 60(cm3)
