人教版七年级数学下册7.2.2用坐标表示平移课件(18张PPT)
文档属性
| 名称 | 人教版七年级数学下册7.2.2用坐标表示平移课件(18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 585.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-24 08:47:15 | ||
图片预览





文档简介
(共18张PPT)
7.2 坐标方法的简单应用
第七章 平面直角坐标系
7.2.2 用坐标表示平移
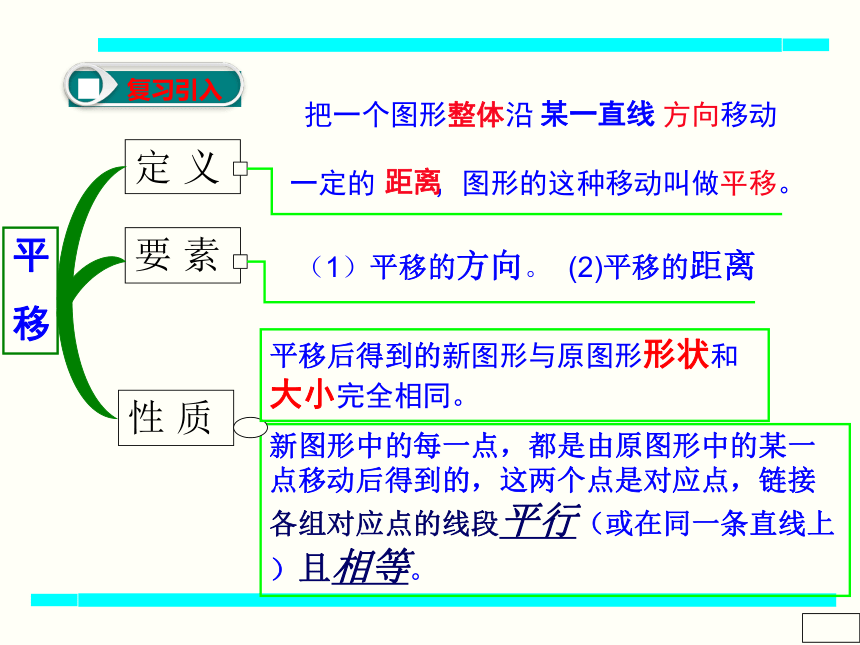
把一个图形整体沿 方向移动
一定的 ,图形的这种移动叫做平移。
平
移
新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,链接各组对应点的线段平行(或在同一条直线上)且相等。
定 义
(1)平移的方向。 (2)平移的距离
平移后得到的新图形与原图形形状和大小完全相同。
某一直线
距离
7.2.2坐标的平移
学习目标:
1、掌握坐标变化与图形之间的关系;能利用点
的平移规律将平面图形平移。
2、会根据图形上点的坐标的变化,来判断图形的
移动过程。
学习重点:掌握坐标变化与图形平移的关系。
学习难点:利用坐标变化与图形平移的关 系解
决实际问题。
y
x
5
4
2
6
4
3
3
2
1
0
-1
-2
-3
-4
-5
6
5
-6
-5
-4
-3
-2
-1
1
探究1 在右图的平面直角坐标系中,将点A(-2,-3)
(1) 向右平移5个单位得到点A1,
(2) 向左平移3个单位得到点A2 ,
(3) 向上平移4个单位得到点A3,
(4) 向下平移3个单位得到的A4 ,
在图上标出这四个点,并分别写出它们的坐标。
A
A1
A2
A3
A4
左右平移
上下平移
横坐标:左减右加
纵坐标:上加下减
(3,-3)
(-5,-3)
(-2,1)
(-2,-4)
纵坐标 -1
纵坐标 +4
横坐标 -3
横坐标 +5
A(-2,-3)
向右平移5个单位
A(-2,-3)
向左平移3个单位
A1
A2
A(-2,-3)
A(-2,-3)
向上平移4个单位
向下平移1个单位
A3
A4
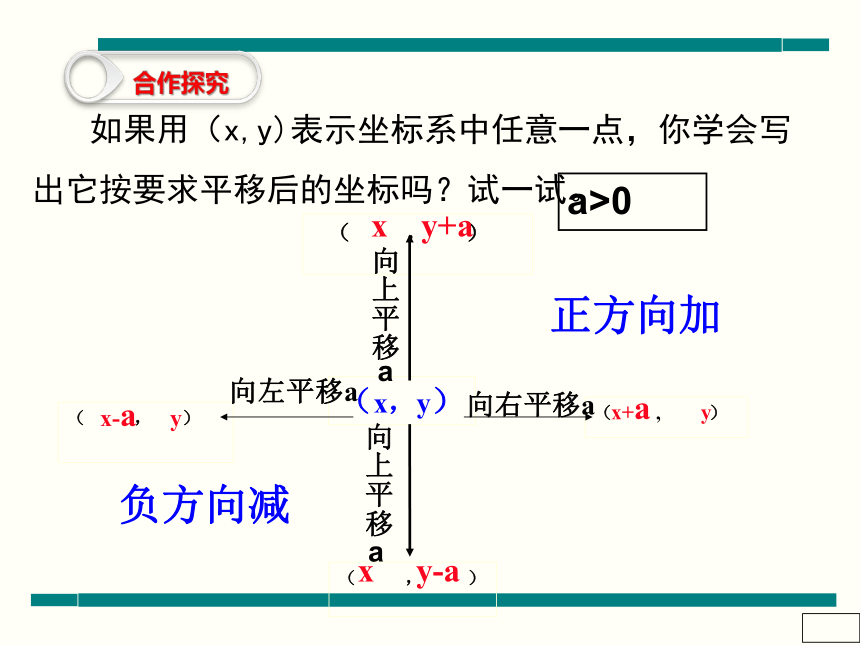
如果用(x,y)表示坐标系中任意一点,你学会写出它按要求平移后的坐标吗?试一试。
(x,y)
( , )
( , )
( , )
向左平移a
向右平移a
向上平移
向上平移
( , )
a
a
x y+a
x+a y
x-a y
x y-a
a>0
正方向加
负方向减
平移规律:
左右平移,横坐标左减右加
上下平移,纵坐标上加下减
一句话:正方向加,负方向减
横坐标:
纵坐标:
(3,-3)
(-5,-3)
(-2,1)
(-2,-4)
纵坐标 -1
纵坐标 +4
横坐标 -3
横坐标 +5
A(-2,-3)
向右平移5个单位
A(-2,-3)
向左平移3个单位
A1
A2
A(-2,-3)
A(-2,-3)
向上平移4个单位
向下平移1个单位
A3
A4
增加右平移
减小左平移
增加上平移
减小下平移
逆向思维:
一句话:坐标增加向正方向移动,坐标减小向负方向移动。
《赶花》读后感及心得400字
我们不能今天等明天,明天等后天,时光流逝,将一事无成。下面是XXXX为您整理的“”,仅供参考,希望您喜欢! 1
看了《赶花》这一篇作文后,我的感悟很深。
这篇作文通过叙述养蜂工的生活,说明了:“只能人赶花,不能花赶人”的道理,启示我在学习、生活上也要有“赶”的精神,“赶”了就会有收获;“等”,今天等明天,明天等后天,时光流逝,将一事无成。
我对这句话感悟很深。众所周知,骄傲的同学最终会落后,而持之以恒勤奋学习的同学成绩必然会领先。
骄傲的同学总觉得自己学得差不多了,所以就“停”了下来,不去想前“赶”。正相反学习虚心的同学总觉得学不够,所以就不停的去“赶”,成绩也就上升了。
我自己在学习中虽然没有“等”但“赶”得劲头也不足。自从看了这篇文章后,我下定决心从明天开始,不!从现在开始,用养蜂工的那种“赶的精神学习,让自己学习成绩步步高升。
希望各位同学也用”赶花”的精神学习,不能让花等你,正所谓:花儿凋谢不再开,光阴一去不在来! 3 一本好书能给人带来智慧和力量。它就像一艘船,带领
我们从狭隘的地方,驰向无限广阔的生活海洋。读四年级时,爸爸给我买了一本课
例1、(1)将正方形ABCD先向下平移5个单位长度,再向右平移6个单位长度,画出平移后的图形,并指出平移后
的正方形A1B1C1D1各顶点的坐标。
B
A
C
D
A1
B1
C1
D1
A(-3,4)
B(-3,2)
C(-1,2)
D(-1,4)
A1( 3,-1)
B1(3,-3)
C1(5,-3)
D1(5,-1)
横 +6
纵 -5
纵 -5
纵 -5
纵 -5
横 +6
横 +6
横 +6
(2)正方形ABCD先向下平移5个单位长度,再向右平移6个单位长度.试问:如果点P(x,y)是正方形内的一点,平移后它的对应点P1的坐标如何表示?
归纳:
对一个图形进行平移时,该图形上所有的点的坐标都会发生相应的变化,所以图形的平移一般转化为点的平移。
P1(x-5,y+6)
例1、(1)将正方形ABCD的各定点横坐标不变,纵坐标都减小5个单位长度,得到新的正方形A1B1C1D1,写出新正方形各顶点的坐标。说一说原图形到新图形做了怎样的移动?
B
A
C
D
A(-3,4)
B(-3,2)
C(-1,2)
D(-1,4)
A1(- 3,-1)
B1(-3,-3)
C1(-1,-3)
D1(-1,-1)
纵 -5
纵 -5
纵 -5
纵 -5
图形的平移
A1
B1
C1
D1
A(-3,4)
B(-3,2)
C(-1,2)
D(-1,4)
A1( 3,4)
B1(3,2)
C1(5,2)
D1(5,4)
横 +6
横 +6
横 +6
横 +6
图形的平移
例1、(1)正方形ABCD各定点横坐标增加6个单位长度,纵坐标不变,得到新的正方形A1B1C1D1,写出新正方形各顶点的坐标。说一说原图形到新图形做了怎样的移动?
归纳:在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向 (或向 )平移 个单位长度;
如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向 (或 )平 移个单位长度。
右
左
上
下
a
a
简单说成: 横坐标左减右加,纵坐标上加下减
因此,平移会引起点的坐标变化,同时,通过点的坐标变化可以看出点的平移过程。
2、 △DEF是由△ABC平移得到的,如果A(1,1)对应点D(1,2)则B(-1,0),C(2,-1)的对应点E、F 的坐标分别是 , 。
1、点C(-2,5)向 平移 个单位长度得到D(-2,3);点B(6,3)是由点A(-2,3)向 平移 个单位长度得到的。
8
2
右
下
(-1,1)
(2,1)
3、将点A(-4,-5)向上平移3个单位长度,再向左平移3个单位长度后所得坐标为 。
(-1,-8)
4、将点M(a,b)向右平移2个单位长度,再向下平移3个单位长度后,其坐标变为(1,-6),则a= ,b= 。
-1
-3
5、将点P(m+2,2m+4)向右平移1个单位得到点Q,且Q点在y轴上,那么Q点坐标是 P点坐标是 。
(0,-2)
(-1,-2)
课堂小结
本节课我们学习了哪些知识?
解题中,我们要注意哪些方面?你有什么解题技巧吗?
对于这节课的知识,你还有哪些疑惑?
7.2 坐标方法的简单应用
第七章 平面直角坐标系
7.2.2 用坐标表示平移
把一个图形整体沿 方向移动
一定的 ,图形的这种移动叫做平移。
平
移
新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,链接各组对应点的线段平行(或在同一条直线上)且相等。
定 义
(1)平移的方向。 (2)平移的距离
平移后得到的新图形与原图形形状和大小完全相同。
某一直线
距离
7.2.2坐标的平移
学习目标:
1、掌握坐标变化与图形之间的关系;能利用点
的平移规律将平面图形平移。
2、会根据图形上点的坐标的变化,来判断图形的
移动过程。
学习重点:掌握坐标变化与图形平移的关系。
学习难点:利用坐标变化与图形平移的关 系解
决实际问题。
y
x
5
4
2
6
4
3
3
2
1
0
-1
-2
-3
-4
-5
6
5
-6
-5
-4
-3
-2
-1
1
探究1 在右图的平面直角坐标系中,将点A(-2,-3)
(1) 向右平移5个单位得到点A1,
(2) 向左平移3个单位得到点A2 ,
(3) 向上平移4个单位得到点A3,
(4) 向下平移3个单位得到的A4 ,
在图上标出这四个点,并分别写出它们的坐标。
A
A1
A2
A3
A4
左右平移
上下平移
横坐标:左减右加
纵坐标:上加下减
(3,-3)
(-5,-3)
(-2,1)
(-2,-4)
纵坐标 -1
纵坐标 +4
横坐标 -3
横坐标 +5
A(-2,-3)
向右平移5个单位
A(-2,-3)
向左平移3个单位
A1
A2
A(-2,-3)
A(-2,-3)
向上平移4个单位
向下平移1个单位
A3
A4
如果用(x,y)表示坐标系中任意一点,你学会写出它按要求平移后的坐标吗?试一试。
(x,y)
( , )
( , )
( , )
向左平移a
向右平移a
向上平移
向上平移
( , )
a
a
x y+a
x+a y
x-a y
x y-a
a>0
正方向加
负方向减
平移规律:
左右平移,横坐标左减右加
上下平移,纵坐标上加下减
一句话:正方向加,负方向减
横坐标:
纵坐标:
(3,-3)
(-5,-3)
(-2,1)
(-2,-4)
纵坐标 -1
纵坐标 +4
横坐标 -3
横坐标 +5
A(-2,-3)
向右平移5个单位
A(-2,-3)
向左平移3个单位
A1
A2
A(-2,-3)
A(-2,-3)
向上平移4个单位
向下平移1个单位
A3
A4
增加右平移
减小左平移
增加上平移
减小下平移
逆向思维:
一句话:坐标增加向正方向移动,坐标减小向负方向移动。
《赶花》读后感及心得400字
我们不能今天等明天,明天等后天,时光流逝,将一事无成。下面是XXXX为您整理的“”,仅供参考,希望您喜欢! 1
看了《赶花》这一篇作文后,我的感悟很深。
这篇作文通过叙述养蜂工的生活,说明了:“只能人赶花,不能花赶人”的道理,启示我在学习、生活上也要有“赶”的精神,“赶”了就会有收获;“等”,今天等明天,明天等后天,时光流逝,将一事无成。
我对这句话感悟很深。众所周知,骄傲的同学最终会落后,而持之以恒勤奋学习的同学成绩必然会领先。
骄傲的同学总觉得自己学得差不多了,所以就“停”了下来,不去想前“赶”。正相反学习虚心的同学总觉得学不够,所以就不停的去“赶”,成绩也就上升了。
我自己在学习中虽然没有“等”但“赶”得劲头也不足。自从看了这篇文章后,我下定决心从明天开始,不!从现在开始,用养蜂工的那种“赶的精神学习,让自己学习成绩步步高升。
希望各位同学也用”赶花”的精神学习,不能让花等你,正所谓:花儿凋谢不再开,光阴一去不在来! 3 一本好书能给人带来智慧和力量。它就像一艘船,带领
我们从狭隘的地方,驰向无限广阔的生活海洋。读四年级时,爸爸给我买了一本课
例1、(1)将正方形ABCD先向下平移5个单位长度,再向右平移6个单位长度,画出平移后的图形,并指出平移后
的正方形A1B1C1D1各顶点的坐标。
B
A
C
D
A1
B1
C1
D1
A(-3,4)
B(-3,2)
C(-1,2)
D(-1,4)
A1( 3,-1)
B1(3,-3)
C1(5,-3)
D1(5,-1)
横 +6
纵 -5
纵 -5
纵 -5
纵 -5
横 +6
横 +6
横 +6
(2)正方形ABCD先向下平移5个单位长度,再向右平移6个单位长度.试问:如果点P(x,y)是正方形内的一点,平移后它的对应点P1的坐标如何表示?
归纳:
对一个图形进行平移时,该图形上所有的点的坐标都会发生相应的变化,所以图形的平移一般转化为点的平移。
P1(x-5,y+6)
例1、(1)将正方形ABCD的各定点横坐标不变,纵坐标都减小5个单位长度,得到新的正方形A1B1C1D1,写出新正方形各顶点的坐标。说一说原图形到新图形做了怎样的移动?
B
A
C
D
A(-3,4)
B(-3,2)
C(-1,2)
D(-1,4)
A1(- 3,-1)
B1(-3,-3)
C1(-1,-3)
D1(-1,-1)
纵 -5
纵 -5
纵 -5
纵 -5
图形的平移
A1
B1
C1
D1
A(-3,4)
B(-3,2)
C(-1,2)
D(-1,4)
A1( 3,4)
B1(3,2)
C1(5,2)
D1(5,4)
横 +6
横 +6
横 +6
横 +6
图形的平移
例1、(1)正方形ABCD各定点横坐标增加6个单位长度,纵坐标不变,得到新的正方形A1B1C1D1,写出新正方形各顶点的坐标。说一说原图形到新图形做了怎样的移动?
归纳:在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向 (或向 )平移 个单位长度;
如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向 (或 )平 移个单位长度。
右
左
上
下
a
a
简单说成: 横坐标左减右加,纵坐标上加下减
因此,平移会引起点的坐标变化,同时,通过点的坐标变化可以看出点的平移过程。
2、 △DEF是由△ABC平移得到的,如果A(1,1)对应点D(1,2)则B(-1,0),C(2,-1)的对应点E、F 的坐标分别是 , 。
1、点C(-2,5)向 平移 个单位长度得到D(-2,3);点B(6,3)是由点A(-2,3)向 平移 个单位长度得到的。
8
2
右
下
(-1,1)
(2,1)
3、将点A(-4,-5)向上平移3个单位长度,再向左平移3个单位长度后所得坐标为 。
(-1,-8)
4、将点M(a,b)向右平移2个单位长度,再向下平移3个单位长度后,其坐标变为(1,-6),则a= ,b= 。
-1
-3
5、将点P(m+2,2m+4)向右平移1个单位得到点Q,且Q点在y轴上,那么Q点坐标是 P点坐标是 。
(0,-2)
(-1,-2)
课堂小结
本节课我们学习了哪些知识?
解题中,我们要注意哪些方面?你有什么解题技巧吗?
对于这节课的知识,你还有哪些疑惑?
