五年级下册数学课件-2.3第2课时 奇偶性 人教版(共23张PPT)
文档属性
| 名称 | 五年级下册数学课件-2.3第2课时 奇偶性 人教版(共23张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-24 14:01:28 | ||
图片预览




文档简介
(共23张PPT)
第2课时 奇偶性
一、游戏激趣,感知规律
8次,11次,100次,119次杯口朝上还是下
二、游戏激趣,感知规律
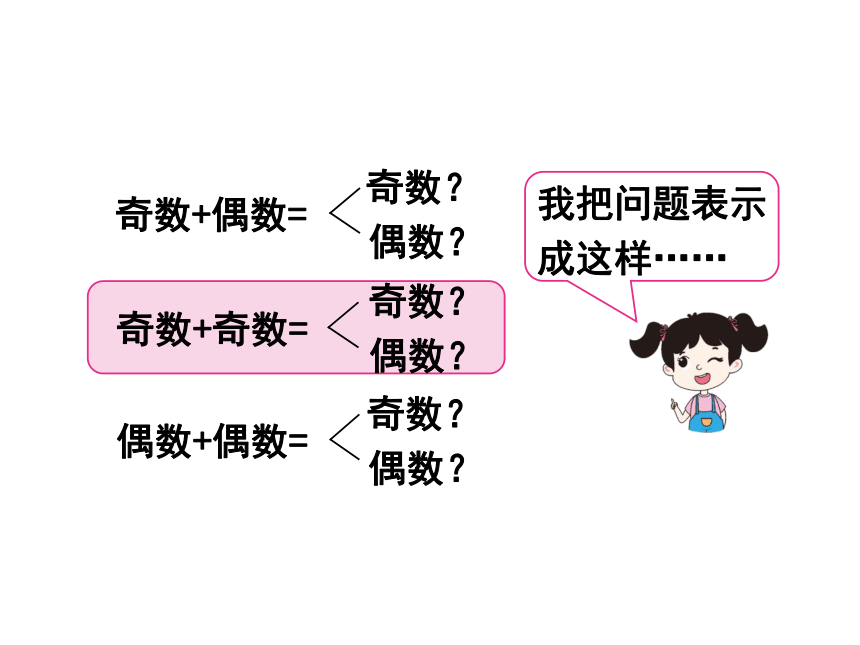
奇数与偶数的和是奇数还是偶数?奇数与奇数的和是奇数还是偶数?偶数与偶数的和呢?
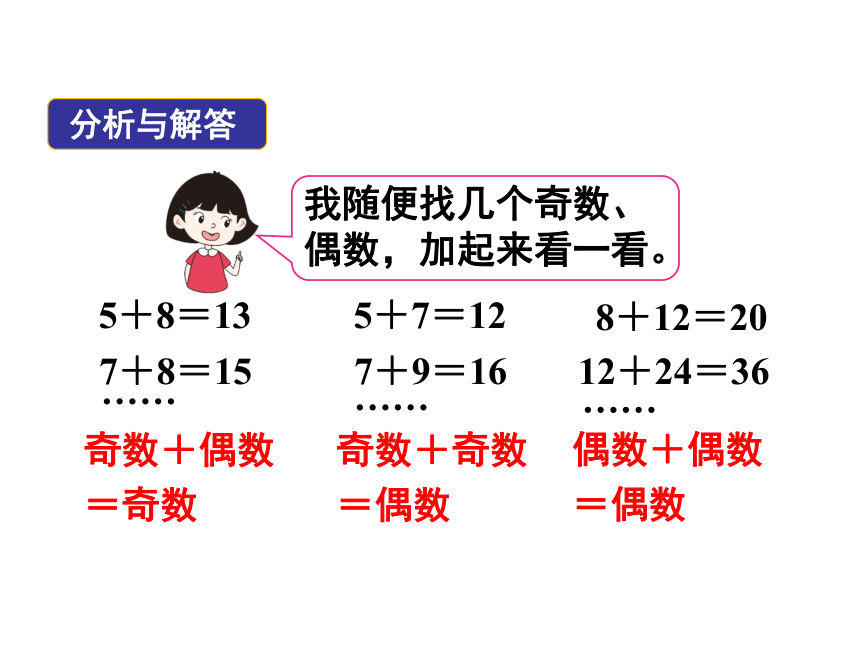
5+7=12
8+12=20
……
……
奇数+奇数
=偶数
偶数+偶数
=偶数
5+8=13
……
奇数+偶数
=奇数
7+9=16
12+24=36
7+8=15
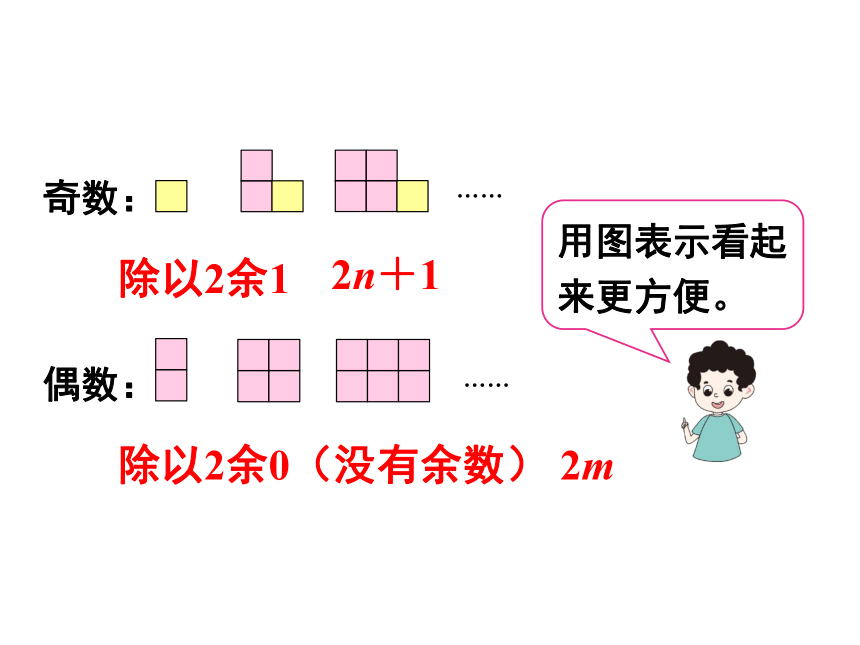
除以2余1
除以2余0(没有余数)
用图表示看起来更方便。
2n+1
2m
除以2余1
所以,奇数+偶数=奇数
2n+1
2m
(2n+1) +2 m=2 (n+ m ) +1
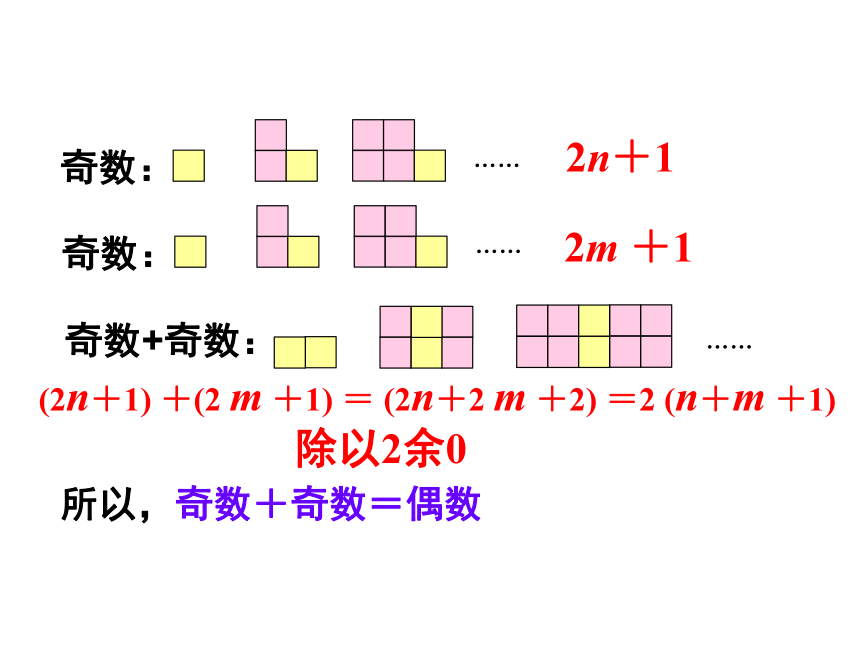
除以2余1
除以2余0
所以,奇数+奇数=偶数
2n+1
(2n+1) +(2 m +1) = (2n+2 m +2) =2 (n+m +1)
2m +1
除以2余0
所以,偶数+偶数=偶数
2n
2m
2n+ 2m =2( n+ m)
除以2余0
除以2余0
我可以再找一些大数试一试。
这个结论正确吗?
123+222=345
319+534=853
325+127=452
533+317=850
434+318=752
620+312=932
奇数+偶数=奇数
奇数+奇数=偶数
偶数+偶数=偶数
所以,以上结论正确!
三、拓展提升,深化认识
偶数+偶数+偶数=
偶数+偶数+偶数+偶数=
偶数+偶数+……+偶数=
偶数
偶数
偶数
结论:无论多少个偶数相加的和都是偶数。
奇数+奇数+奇数=
奇数+奇数+奇数+奇数=
奇数+奇数+奇数+奇数+奇数=
奇数
偶数
奇数
10个奇数相加的和=
偶数
结论:奇数个奇数相加的和是奇数。
偶数个奇数相加的和是偶数。
拓展提升
归纳总结
多个自然数相加,就看加数中奇数的个数,如果加数中有奇数个奇数,和就是奇数;有偶数个奇数,和就是偶数。
四、运用规律,内化规律
1. 1+2+3+4+……+98+99 ,如果不计算,你能很快说出这道算式的和是奇数还是偶数吗?
1到99中有50个奇数,偶数个奇数的和是偶数,其它偶数的和也是偶数 ,所以1+2+3+4+……+98+99的和是偶数。
30个学生要分成甲、乙两队。如果甲队人数为奇数,乙队人数为奇数还是偶数?如果甲队人数为偶数呢?
2.
3. 奇数与奇数的积是奇数还是偶数?奇数与偶数的积是奇数还是偶数?偶数与偶数的积呢?
5×7=35
7×9=63
5×8=40
7×8=56
8×12=96
14×24=336
……
……
……
奇数×奇数=奇数
奇数×偶数=偶数
偶数×偶数=偶数
4. 探索 6 的倍数特征,并记录你探索的过程和结果。
6的倍数的特征:各位上的数的和是3的倍数且个位上的数是偶数。
探究过程:先写出一些6的倍数,然后观察它的个位上的数和各个数位上的数的和的特点。
五、课堂小结
同学们,今天的数学课你们有哪些收获呢?
?备选练习
一、不计算,直接判断结果是奇数还是偶数。
46 + 27( ) 34 + 108 ( )
13×72 ( ) 268 × 54 ( )
89 +415 ( ) 71 × 67 ( )
奇数
奇数
偶数
偶数
偶数
偶数
二、有48个桃子,把它们放在13个篮子
里,每个篮子里只能放奇数个桃子,
这件事你能办到吗?
不能办到。13个奇数的和一定是奇数,不可能是偶数48。
第2课时 奇偶性
一、游戏激趣,感知规律
8次,11次,100次,119次杯口朝上还是下
二、游戏激趣,感知规律
奇数与偶数的和是奇数还是偶数?奇数与奇数的和是奇数还是偶数?偶数与偶数的和呢?
5+7=12
8+12=20
……
……
奇数+奇数
=偶数
偶数+偶数
=偶数
5+8=13
……
奇数+偶数
=奇数
7+9=16
12+24=36
7+8=15
除以2余1
除以2余0(没有余数)
用图表示看起来更方便。
2n+1
2m
除以2余1
所以,奇数+偶数=奇数
2n+1
2m
(2n+1) +2 m=2 (n+ m ) +1
除以2余1
除以2余0
所以,奇数+奇数=偶数
2n+1
(2n+1) +(2 m +1) = (2n+2 m +2) =2 (n+m +1)
2m +1
除以2余0
所以,偶数+偶数=偶数
2n
2m
2n+ 2m =2( n+ m)
除以2余0
除以2余0
我可以再找一些大数试一试。
这个结论正确吗?
123+222=345
319+534=853
325+127=452
533+317=850
434+318=752
620+312=932
奇数+偶数=奇数
奇数+奇数=偶数
偶数+偶数=偶数
所以,以上结论正确!
三、拓展提升,深化认识
偶数+偶数+偶数=
偶数+偶数+偶数+偶数=
偶数+偶数+……+偶数=
偶数
偶数
偶数
结论:无论多少个偶数相加的和都是偶数。
奇数+奇数+奇数=
奇数+奇数+奇数+奇数=
奇数+奇数+奇数+奇数+奇数=
奇数
偶数
奇数
10个奇数相加的和=
偶数
结论:奇数个奇数相加的和是奇数。
偶数个奇数相加的和是偶数。
拓展提升
归纳总结
多个自然数相加,就看加数中奇数的个数,如果加数中有奇数个奇数,和就是奇数;有偶数个奇数,和就是偶数。
四、运用规律,内化规律
1. 1+2+3+4+……+98+99 ,如果不计算,你能很快说出这道算式的和是奇数还是偶数吗?
1到99中有50个奇数,偶数个奇数的和是偶数,其它偶数的和也是偶数 ,所以1+2+3+4+……+98+99的和是偶数。
30个学生要分成甲、乙两队。如果甲队人数为奇数,乙队人数为奇数还是偶数?如果甲队人数为偶数呢?
2.
3. 奇数与奇数的积是奇数还是偶数?奇数与偶数的积是奇数还是偶数?偶数与偶数的积呢?
5×7=35
7×9=63
5×8=40
7×8=56
8×12=96
14×24=336
……
……
……
奇数×奇数=奇数
奇数×偶数=偶数
偶数×偶数=偶数
4. 探索 6 的倍数特征,并记录你探索的过程和结果。
6的倍数的特征:各位上的数的和是3的倍数且个位上的数是偶数。
探究过程:先写出一些6的倍数,然后观察它的个位上的数和各个数位上的数的和的特点。
五、课堂小结
同学们,今天的数学课你们有哪些收获呢?
?备选练习
一、不计算,直接判断结果是奇数还是偶数。
46 + 27( ) 34 + 108 ( )
13×72 ( ) 268 × 54 ( )
89 +415 ( ) 71 × 67 ( )
奇数
奇数
偶数
偶数
偶数
偶数
二、有48个桃子,把它们放在13个篮子
里,每个篮子里只能放奇数个桃子,
这件事你能办到吗?
不能办到。13个奇数的和一定是奇数,不可能是偶数48。
