六年级下册数学一课一练-1.4圆锥的体积 北师大版(含答案)
文档属性
| 名称 | 六年级下册数学一课一练-1.4圆锥的体积 北师大版(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 83.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-24 17:16:01 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
六年级下册数学一课一练-1.4圆锥的体积
一、单选题
1.底面积和体积分别相等的圆柱和圆锥,如果圆锥的高是15厘米,那么圆柱的高是(
)厘米。
A. 5 B. 15 C. 30 D. 45
2.一个圆锥的体积是12立方厘米,底面积是4平方厘米,高是(
)厘米.
A. 3 B. 6 C. 9 D. 12
3.
一个圆锥和一个圆柱的底面积相等,体积也相等.已知圆柱的高是1厘米,圆锥的高是( )厘米.
A. B. 1 C. 3
4.圆锥的底面积是16平方厘米,高6厘米,它的体积是(
)
A. 96立方厘米 B. 23立方厘米 C. 69立方厘米 D. 32立方厘米
二、判断题
5.圆柱的体积等于圆锥体积的3倍。
6.判断对错。
如果圆锥的体积是圆柱体积的
,那么它们一定等底等高。
7.判断对错.
圆锥的体积总是圆柱体积的
.
8.从一个圆锥高的
处切下一个圆锥,这个圆锥的体积是原来体积的
。
三、填空题
9.一堆稻谷堆成圆锥体。量得底面半径是3米,高是1.5米。这堆稻谷的体积有________立方米。
10.一个圆锥形沙堆量得底面周长是12.56米,高1.5米,这个沙堆的体积是________立方米。
11.圆锥的底面半径是4厘米,体积是50.24立方厘米,这个圆锥的高是________厘米。
12.一个直圆锥的体积是120立方厘米,将圆锥体沿高的
处横截成圆台,将这个圆台放入圆柱形纸盒,纸盒的容积至少是________立方厘米.
四、解答题
13.一个圆锥形物体,底面直径和高都是12cm。它的体积是多少?
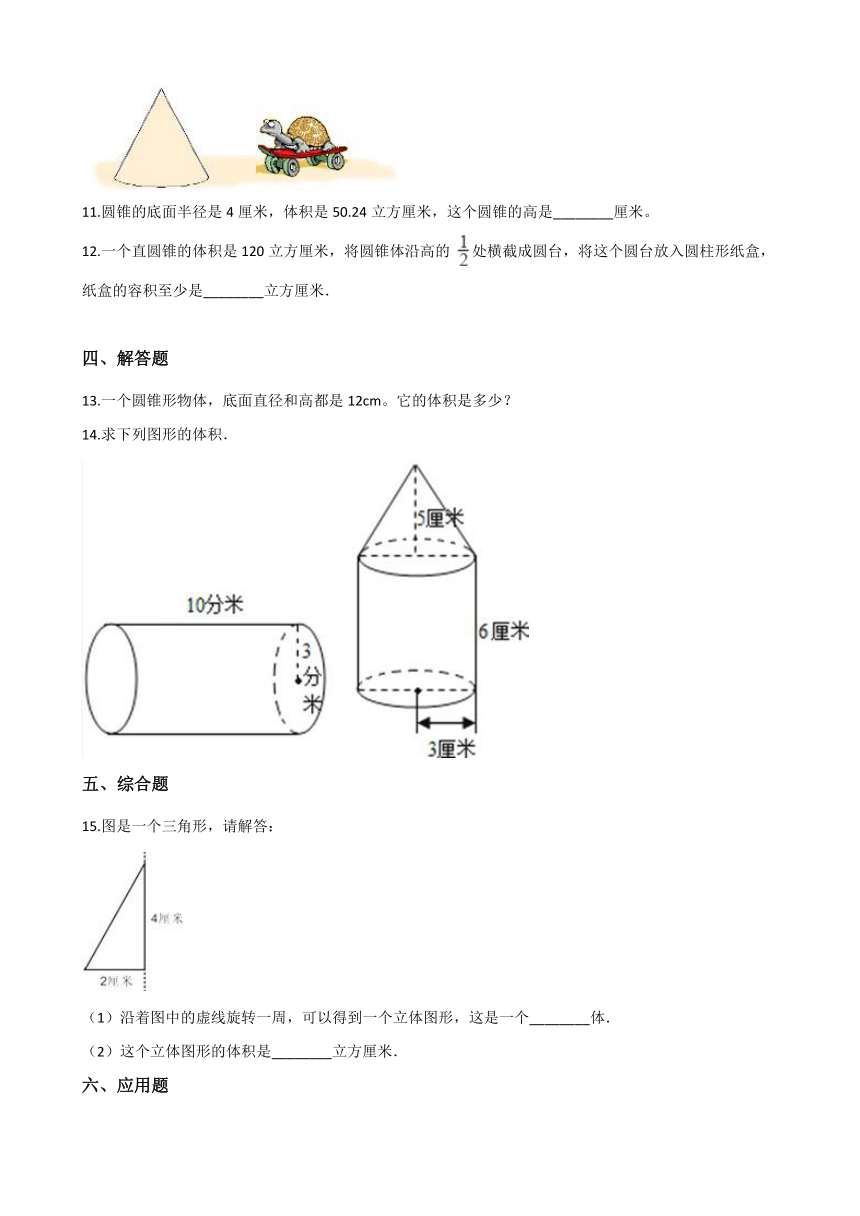
14.求下列图形的体积.
五、综合题
15.图是一个三角形,请解答:
(1)沿着图中的虚线旋转一周,可以得到一个立体图形,这是一个________体.
(2)这个立体图形的体积是________立方厘米.
六、应用题
16.一个圆锥形沙堆,底面周长是18.84m,高2m.如果每立方米的沙质量为1.5吨.这堆沙子的质量共有多少吨?
参考答案
一、单选题
1.【答案】A
【解析】【解答】当圆柱和圆锥的底面积和体积相等时,两者的高之比是1:3,当圆锥的高是15cm时,圆柱的高是5cm。
故答案为:A.
【分析】底面积和体积分别相等的圆柱和圆锥,圆柱的高是圆锥高的,据此解答.
2.【答案】
C
【解析】【解答】解:12×3÷4,
=36÷4,
=9(厘米);
答:这个圆锥的高是9厘米。
【分析】根据题意,根据圆锥的体积公式=
×底面积×高,用圆锥的体积乘3再除以底面积即可得到这个圆锥的高,列式解答即可得到答案。
故选:C
3.【答案】
C
【解析】【解答】解:设圆柱和圆锥的体积相等为V,底面积相等为S,则:
圆柱的高为:;
圆锥的高为:;
所以圆柱的高与圆锥的高的比是::=1:3,
因为圆柱的高是1厘米,
所以圆锥的高为:3×1=3(厘米),
答:圆锥的高是3厘米.
故选:C.
【分析】设圆柱和圆锥的体积相等为V,底面积相等为S,由此利用圆柱和圆锥的体积公式推理得出它们的高的比,即可解答此题.
4.【答案】
D
【解析】【解答】16×6×=32(立方厘米)
故答案为:D
【分析】圆锥的体积=底面积×高×,
由此根据圆锥的体积公式列式计算即可.
二、判断题
5.【答案】错误
【解析】【解答】等底等高的圆柱的体积等于圆锥体积的3倍,原题说法错误.
故答案为:错误.
【分析】一个圆柱的体积是与它等底等高的圆锥体积的3倍,原题没有注明“等底等高”或其它的条件,只说“圆柱的体积是圆锥体积的3倍”是错误的,据此判断.
6.【答案】
错误
【解析】【解答】设圆柱的底面积为12,高为3,则圆柱的体积为:12×3=36;
圆锥的底面积为6,高为6,则圆锥的体积为:×6×6=12;此时圆锥的体积是圆柱的体积的,但是它们的底面积与高都不相等。
故答案为:错误。
【分析】解决此类问题,采用举反例的方法是一种有效的简洁的方法,这要求学生要熟练掌握圆柱和圆锥的体积公式。
7.【答案】
错误
【解析】【解答】圆锥的体积是等底等高的圆柱体积的.
故答案为:错误。
【分析】根据等底等高的圆锥体积与圆柱体积的关系:等底等高的圆柱体积是圆锥体积的3倍,据此解答即可。
8.【答案】错误
【解析】【解答】根据题干分析可得:切下的小圆锥的底面直径:原来的圆锥的底面直径=1:2,
设小圆锥的底面直径为1,高为1,则原来圆锥的底面直径为2,高为2;
所以小圆锥的体积为:×π×()2×1=;
原来大圆锥的体积为:×π×()2×2=;
所以小圆锥体积与原来大圆锥的体积之比是:=1:8,原题说法错误.
故答案为:错误.
【分析】沿圆锥的高线画出这个圆锥的横切面如图所示,
则AB是这个圆锥的底面直径,CD就是切下的圆锥的底面直径,因为OE=OF,所以可得CD:AB=OE:OF=1:2;由此设切下的小圆锥的底面直径CD为1,则原来的圆锥的底面直径就是2,根据圆锥的体积=×底面积×高,即可得出它们的体积倍数关系进行判断.
三、填空题
9.【答案】14.13
【解析】【解答】解:
(立方米)
答:这堆稻谷的体积有14.13立方米。
【分析】
10.【答案】
6.28
【解析】【解答】解:r=12.56÷2÷3.14=2(米)
(立方米)
答:这个沙堆的体积为6.28立方米。
【分析】
11.【答案】
3
【解析】【解答】圆锥的高是:50.24×3÷(3.14×4 )
=50.24×3÷50.24
=3(厘米)
答:这个圆锥的高是3厘米.
故答案为:3
【分析】圆锥的体积:V=
πr h,由此可得圆锥的高=体积×3÷(πr )代入数据即可计算出这个圆锥的高。
12.【答案】180
【解析】【解答】解:设圆锥的高是2h,则圆柱的高是h;它们的底面积是S,
圆锥的体积:×S×2h=Sh;
圆柱的体积是:Sh;
圆锥和圆柱的体积比是:Sh:Sh=2:3;
因为圆锥的体积是120立方厘米,所以圆柱的体积是120÷2×3=180(立方厘米)
故答案为:180
【分析】要求这个纸盒的体积的最小值,则这个圆柱形容器的高是圆锥高的一半,底面积与圆锥的底面积相等,由此根据圆锥和圆柱的体积公式先求出它们的体积之比即可解答.
四、解答题
13.【答案】12÷2=6(cm)
×3.14×62
×12=452.16(cm3)
答:它的体积是452.16cm3
。
【解析】【分析】圆锥体的体积=×底面积×高,即πr2h,代入数据即可。
14.【答案】解:①3.14×32×10
=3.14×9×10
=3.14×90
=282.6(立方分米),
答:圆柱的体积是1570立方分米.
②3.14×32×6+
×3.14×32×5
=3.14×9×6+×3.14×3×5
=169.56+47.1
=216.66(立方厘米);
答:这个立体图形的体积是216.66立方厘米。
【解析】【分析】①根据圆柱的体积公式V=sh=πr2h
,
代入数据解答即可.②这个立体图形的上部是圆锥,下部是圆柱体,圆柱体的底面半径是3厘米,高是6厘米,圆锥的高是5厘米,利用圆柱的体积公式v=sh,和圆锥的体积公式v=
sh,分别求出它们的体积合并起来即可。
五、综合题
15.【答案】(1)圆锥
(2)16.75
【解析】【解答】解:(1)沿着图中的虚线旋转一周,可以得到一个立体图形,这个立体图形叫做圆锥.
·(2)圆锥的体积=
×3.14×22×4
=
×3.14×4×4
=
×50.24
≈16.75(立方厘米);
答:这个立体图形的体积是16.75立方厘米.
故答案为:圆锥、16.75.
【分析】(1)沿着图中的虚线旋转一周,可以得到一个立体图形,这个立体图形叫做圆锥.(2)圆锥的体积=
×底面积×高,圆锥的底面半径和高已知,从而可以求出圆锥的体积.
六、应用题
16.【答案】解:18.84÷3.14÷2=3(m)
(吨)
答:这堆沙子的质量共有28.26吨.
【解析】【分析】用底面周长除以3.14,再除以2求出底面半径,然后用底面积乘高,再乘求出体积,用体积乘每立方米沙的质量即可求出总质量.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
六年级下册数学一课一练-1.4圆锥的体积
一、单选题
1.底面积和体积分别相等的圆柱和圆锥,如果圆锥的高是15厘米,那么圆柱的高是(
)厘米。
A. 5 B. 15 C. 30 D. 45
2.一个圆锥的体积是12立方厘米,底面积是4平方厘米,高是(
)厘米.
A. 3 B. 6 C. 9 D. 12
3.
一个圆锥和一个圆柱的底面积相等,体积也相等.已知圆柱的高是1厘米,圆锥的高是( )厘米.
A. B. 1 C. 3
4.圆锥的底面积是16平方厘米,高6厘米,它的体积是(
)
A. 96立方厘米 B. 23立方厘米 C. 69立方厘米 D. 32立方厘米
二、判断题
5.圆柱的体积等于圆锥体积的3倍。
6.判断对错。
如果圆锥的体积是圆柱体积的
,那么它们一定等底等高。
7.判断对错.
圆锥的体积总是圆柱体积的
.
8.从一个圆锥高的
处切下一个圆锥,这个圆锥的体积是原来体积的
。
三、填空题
9.一堆稻谷堆成圆锥体。量得底面半径是3米,高是1.5米。这堆稻谷的体积有________立方米。
10.一个圆锥形沙堆量得底面周长是12.56米,高1.5米,这个沙堆的体积是________立方米。
11.圆锥的底面半径是4厘米,体积是50.24立方厘米,这个圆锥的高是________厘米。
12.一个直圆锥的体积是120立方厘米,将圆锥体沿高的
处横截成圆台,将这个圆台放入圆柱形纸盒,纸盒的容积至少是________立方厘米.
四、解答题
13.一个圆锥形物体,底面直径和高都是12cm。它的体积是多少?
14.求下列图形的体积.
五、综合题
15.图是一个三角形,请解答:
(1)沿着图中的虚线旋转一周,可以得到一个立体图形,这是一个________体.
(2)这个立体图形的体积是________立方厘米.
六、应用题
16.一个圆锥形沙堆,底面周长是18.84m,高2m.如果每立方米的沙质量为1.5吨.这堆沙子的质量共有多少吨?
参考答案
一、单选题
1.【答案】A
【解析】【解答】当圆柱和圆锥的底面积和体积相等时,两者的高之比是1:3,当圆锥的高是15cm时,圆柱的高是5cm。
故答案为:A.
【分析】底面积和体积分别相等的圆柱和圆锥,圆柱的高是圆锥高的,据此解答.
2.【答案】
C
【解析】【解答】解:12×3÷4,
=36÷4,
=9(厘米);
答:这个圆锥的高是9厘米。
【分析】根据题意,根据圆锥的体积公式=
×底面积×高,用圆锥的体积乘3再除以底面积即可得到这个圆锥的高,列式解答即可得到答案。
故选:C
3.【答案】
C
【解析】【解答】解:设圆柱和圆锥的体积相等为V,底面积相等为S,则:
圆柱的高为:;
圆锥的高为:;
所以圆柱的高与圆锥的高的比是::=1:3,
因为圆柱的高是1厘米,
所以圆锥的高为:3×1=3(厘米),
答:圆锥的高是3厘米.
故选:C.
【分析】设圆柱和圆锥的体积相等为V,底面积相等为S,由此利用圆柱和圆锥的体积公式推理得出它们的高的比,即可解答此题.
4.【答案】
D
【解析】【解答】16×6×=32(立方厘米)
故答案为:D
【分析】圆锥的体积=底面积×高×,
由此根据圆锥的体积公式列式计算即可.
二、判断题
5.【答案】错误
【解析】【解答】等底等高的圆柱的体积等于圆锥体积的3倍,原题说法错误.
故答案为:错误.
【分析】一个圆柱的体积是与它等底等高的圆锥体积的3倍,原题没有注明“等底等高”或其它的条件,只说“圆柱的体积是圆锥体积的3倍”是错误的,据此判断.
6.【答案】
错误
【解析】【解答】设圆柱的底面积为12,高为3,则圆柱的体积为:12×3=36;
圆锥的底面积为6,高为6,则圆锥的体积为:×6×6=12;此时圆锥的体积是圆柱的体积的,但是它们的底面积与高都不相等。
故答案为:错误。
【分析】解决此类问题,采用举反例的方法是一种有效的简洁的方法,这要求学生要熟练掌握圆柱和圆锥的体积公式。
7.【答案】
错误
【解析】【解答】圆锥的体积是等底等高的圆柱体积的.
故答案为:错误。
【分析】根据等底等高的圆锥体积与圆柱体积的关系:等底等高的圆柱体积是圆锥体积的3倍,据此解答即可。
8.【答案】错误
【解析】【解答】根据题干分析可得:切下的小圆锥的底面直径:原来的圆锥的底面直径=1:2,
设小圆锥的底面直径为1,高为1,则原来圆锥的底面直径为2,高为2;
所以小圆锥的体积为:×π×()2×1=;
原来大圆锥的体积为:×π×()2×2=;
所以小圆锥体积与原来大圆锥的体积之比是:=1:8,原题说法错误.
故答案为:错误.
【分析】沿圆锥的高线画出这个圆锥的横切面如图所示,
则AB是这个圆锥的底面直径,CD就是切下的圆锥的底面直径,因为OE=OF,所以可得CD:AB=OE:OF=1:2;由此设切下的小圆锥的底面直径CD为1,则原来的圆锥的底面直径就是2,根据圆锥的体积=×底面积×高,即可得出它们的体积倍数关系进行判断.
三、填空题
9.【答案】14.13
【解析】【解答】解:
(立方米)
答:这堆稻谷的体积有14.13立方米。
【分析】
10.【答案】
6.28
【解析】【解答】解:r=12.56÷2÷3.14=2(米)
(立方米)
答:这个沙堆的体积为6.28立方米。
【分析】
11.【答案】
3
【解析】【解答】圆锥的高是:50.24×3÷(3.14×4 )
=50.24×3÷50.24
=3(厘米)
答:这个圆锥的高是3厘米.
故答案为:3
【分析】圆锥的体积:V=
πr h,由此可得圆锥的高=体积×3÷(πr )代入数据即可计算出这个圆锥的高。
12.【答案】180
【解析】【解答】解:设圆锥的高是2h,则圆柱的高是h;它们的底面积是S,
圆锥的体积:×S×2h=Sh;
圆柱的体积是:Sh;
圆锥和圆柱的体积比是:Sh:Sh=2:3;
因为圆锥的体积是120立方厘米,所以圆柱的体积是120÷2×3=180(立方厘米)
故答案为:180
【分析】要求这个纸盒的体积的最小值,则这个圆柱形容器的高是圆锥高的一半,底面积与圆锥的底面积相等,由此根据圆锥和圆柱的体积公式先求出它们的体积之比即可解答.
四、解答题
13.【答案】12÷2=6(cm)
×3.14×62
×12=452.16(cm3)
答:它的体积是452.16cm3
。
【解析】【分析】圆锥体的体积=×底面积×高,即πr2h,代入数据即可。
14.【答案】解:①3.14×32×10
=3.14×9×10
=3.14×90
=282.6(立方分米),
答:圆柱的体积是1570立方分米.
②3.14×32×6+
×3.14×32×5
=3.14×9×6+×3.14×3×5
=169.56+47.1
=216.66(立方厘米);
答:这个立体图形的体积是216.66立方厘米。
【解析】【分析】①根据圆柱的体积公式V=sh=πr2h
,
代入数据解答即可.②这个立体图形的上部是圆锥,下部是圆柱体,圆柱体的底面半径是3厘米,高是6厘米,圆锥的高是5厘米,利用圆柱的体积公式v=sh,和圆锥的体积公式v=
sh,分别求出它们的体积合并起来即可。
五、综合题
15.【答案】(1)圆锥
(2)16.75
【解析】【解答】解:(1)沿着图中的虚线旋转一周,可以得到一个立体图形,这个立体图形叫做圆锥.
·(2)圆锥的体积=
×3.14×22×4
=
×3.14×4×4
=
×50.24
≈16.75(立方厘米);
答:这个立体图形的体积是16.75立方厘米.
故答案为:圆锥、16.75.
【分析】(1)沿着图中的虚线旋转一周,可以得到一个立体图形,这个立体图形叫做圆锥.(2)圆锥的体积=
×底面积×高,圆锥的底面半径和高已知,从而可以求出圆锥的体积.
六、应用题
16.【答案】解:18.84÷3.14÷2=3(m)
(吨)
答:这堆沙子的质量共有28.26吨.
【解析】【分析】用底面周长除以3.14,再除以2求出底面半径,然后用底面积乘高,再乘求出体积,用体积乘每立方米沙的质量即可求出总质量.
