六年级下册数学课件-6.2第1课时 平面图形的认识与测量(1) 人教版(共32张PPT)
文档属性
| 名称 | 六年级下册数学课件-6.2第1课时 平面图形的认识与测量(1) 人教版(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-24 16:48:53 | ||
图片预览









文档简介
(共32张PPT)
我们已经研究过哪些图形?
图形
平面图形
立体图形
一条线、两条线、三条线、四条线的思路
R·六年级下册
第1课时 平面图形的认识与测量(1)
2. 几何与图形
直线、射线和线段有什么区别?
0
1
2
可以向两边无限延伸
可以向一边无限延伸
不可以延伸
不可度量
不可度量
可度量
端点 延伸 度量
直线
射线
线段
点动成线:
你有什么发现?
射线、线段都是直线的一部分。
射线长还是直线长?
直线、射线都是无限长的,所以无法比较出它们的长短。
要画出一个圆,需要先确定什么?
圆心
半径
O
r
圆的知识
圆心决定圆的位置,半径决定圆的大小。
一个圆有无数条半径,一般用字母r表示;有无数条直径,一般用字母d表示。
1
2
3
同一个圆内,直径的长度是半径的2倍,即:d=2r。
4
圆是轴对称图形,它有无数条对称轴。
一条线
直线
射线
线段
圆
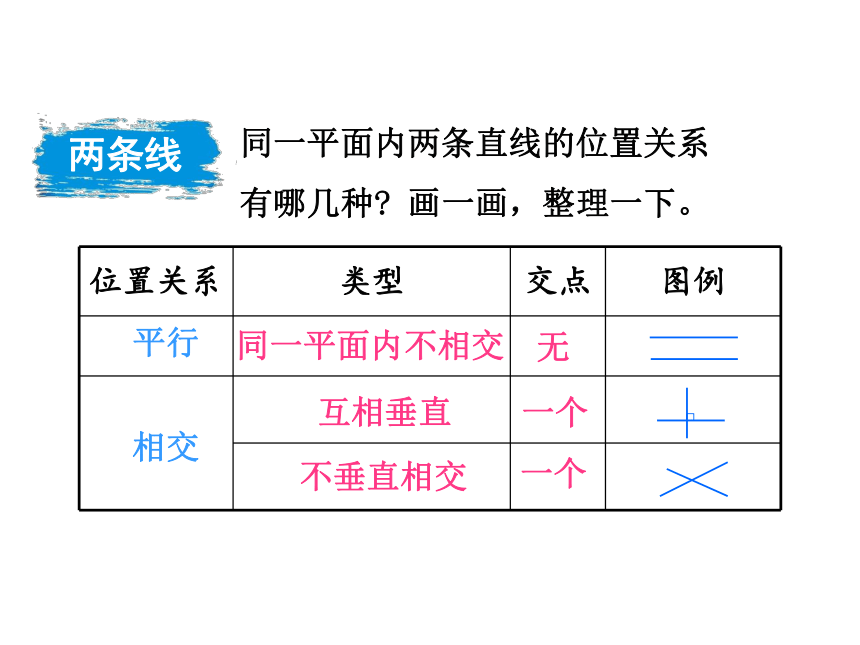
同一平面内两条直线的位置关系有哪几种? 画一画,整理一下。
相交
平行
无
互相垂直
不垂直相交
一个
一个
同一平面内不相交
位置关系 类型 交点 图例
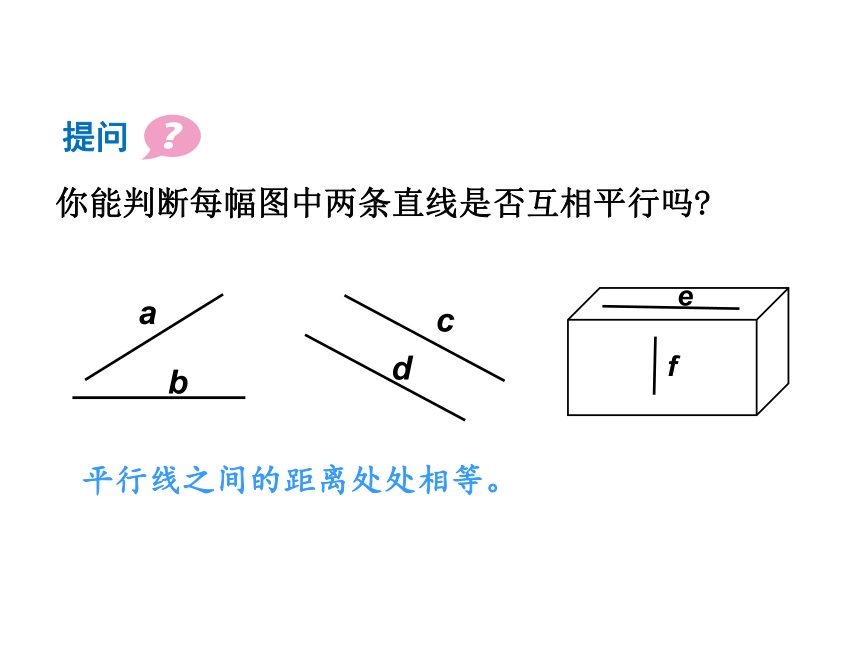
你能判断每幅图中两条直线是否互相平行吗?
平行线之间的距离处处相等。
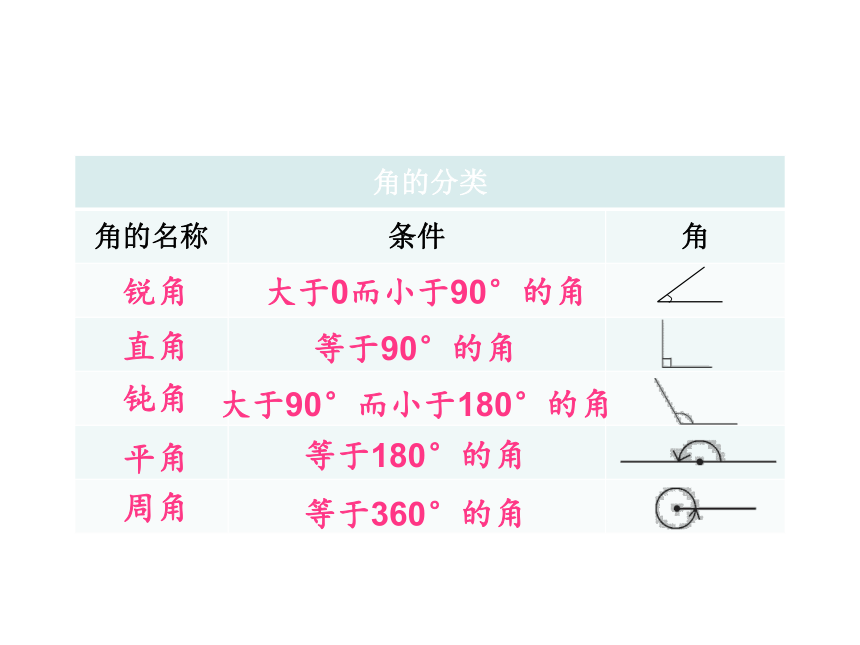
锐角
直角
钝角
平角
周角
大于0而小于90°的角
等于90°的角
大于90°而小于180°的角
等于180°的角
等于360°的角
角的分类
角的名称 条件 角
你能把这些角按照从小到大的顺序排列吗?
在放大镜下看角,它的大小会变化吗? 说明理由。
锐角<直角<钝角<平角<周角
不会变化,因为角的大小与角的两边的长短无关,只与角的两边张开的程度有关。
两条线
平行
相交
角
(同一平面内)
垂直
相交
锐角<直角<钝角<平角<周角
你想到了什么图形?
三角形
扇形
三角形有哪些特征?
1
2
3
稳定性
内角和180°
三角形的任意两边之和大于第三边
三角形可以怎样分类呢?
连一连。
有一个直角,有两条边相等。
只有两个锐角,没有直角。
三个角相等。
没有直角和钝角。
锐角三角形
直角三角形
钝角三角形
等腰三角形
等边三角形
扇形有什么特征呢?
圆上任意两点之间的部分叫做弧。读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形,图中涂色部分就是扇形。
你想到了我们学过的哪些图形?
这些图形的共同特点是什么?
都是由四条直的边围成的图形,都有4个角。
你会给这些四边形分类吗?
做两个一样的平行四边形纸片。把它们重合在一起,将上面的平行四边形绕它的一个顶点旋转180°,再通过平移使它与下面的平行四边形重合。观察两个平行四边形的各条边与各个角,你有什么发现?
1.判断对错,对的画“√”,错的画“×”。
(1)大于90°的角就是钝角。( )
(2)两条直线相交组成的4个角中如果有一个角是直角,那么其他3个角也是直角。( )
(3)任何两个等底等高的梯形都能拼成一个平行四边形。( )
×
√
×
2.在括号里填上合适的计量单位。
km
m2
kg
L
1. 过一点可以画几条直线?过两点可以画几条直线?
无数条
一条
2. 有长度分别为3cm、4cm、5cm、6cm的小棒各一根。哪三根小棒可以围成一个三角形?
3cm、4cm、5cm
4cm、5cm、6cm
3cm、5cm、6cm
3cm、4cm、6cm
三角形任意两边的和大于第三边
3. 一个直角三角形的两个锐角的和是多少度?为什么?
90度。三角形内角和减去一个直角得到两个锐角的和。
锐角三角形的两个锐角和一定大于90°,钝角三角形的两个锐角和一定小于90°。
同学们,今天的数学课你们有哪些收获呢?
1.我会填。
(1)经过一点可以画( )条直线,经过两点可以画( )条直线。
(2)如图,共有( )条直线,( )条射线,( )条线段。
无数
1
1
8
6
(3)一个多边形的内角和是540°,它是( )边形。
(4)(2019·浙江宁波)如图,三角形ABC中,∠A=70°,如果沿图中的虚线剪去∠A,∠1+∠2=( )°。
五
250
2.我会选。(将正确答案的序号填在括号里)
(1)把一张圆形的纸对折两次,折出的角是 ( )角。
A.锐 B.直 C.钝
(2)已知一个三角形的两条边分别长4cm和8cm,那么第三条边可能是( )。
A.12cm B.15cm C.11cm
B
C
(3)下面的角不能用一副三角尺直接画出的是( )。
A.15° B.55° C.75°
B
3.如图,已知∠1=30°,求∠2、∠4和∠5的度数。
∠2=90°-∠1=90°-30°=60°
∠4=180°-∠2-∠3
=180°-60°-90°
=30°
∠5=90°-∠4=90°-30°=60°
我们已经研究过哪些图形?
图形
平面图形
立体图形
一条线、两条线、三条线、四条线的思路
R·六年级下册
第1课时 平面图形的认识与测量(1)
2. 几何与图形
直线、射线和线段有什么区别?
0
1
2
可以向两边无限延伸
可以向一边无限延伸
不可以延伸
不可度量
不可度量
可度量
端点 延伸 度量
直线
射线
线段
点动成线:
你有什么发现?
射线、线段都是直线的一部分。
射线长还是直线长?
直线、射线都是无限长的,所以无法比较出它们的长短。
要画出一个圆,需要先确定什么?
圆心
半径
O
r
圆的知识
圆心决定圆的位置,半径决定圆的大小。
一个圆有无数条半径,一般用字母r表示;有无数条直径,一般用字母d表示。
1
2
3
同一个圆内,直径的长度是半径的2倍,即:d=2r。
4
圆是轴对称图形,它有无数条对称轴。
一条线
直线
射线
线段
圆
同一平面内两条直线的位置关系有哪几种? 画一画,整理一下。
相交
平行
无
互相垂直
不垂直相交
一个
一个
同一平面内不相交
位置关系 类型 交点 图例
你能判断每幅图中两条直线是否互相平行吗?
平行线之间的距离处处相等。
锐角
直角
钝角
平角
周角
大于0而小于90°的角
等于90°的角
大于90°而小于180°的角
等于180°的角
等于360°的角
角的分类
角的名称 条件 角
你能把这些角按照从小到大的顺序排列吗?
在放大镜下看角,它的大小会变化吗? 说明理由。
锐角<直角<钝角<平角<周角
不会变化,因为角的大小与角的两边的长短无关,只与角的两边张开的程度有关。
两条线
平行
相交
角
(同一平面内)
垂直
相交
锐角<直角<钝角<平角<周角
你想到了什么图形?
三角形
扇形
三角形有哪些特征?
1
2
3
稳定性
内角和180°
三角形的任意两边之和大于第三边
三角形可以怎样分类呢?
连一连。
有一个直角,有两条边相等。
只有两个锐角,没有直角。
三个角相等。
没有直角和钝角。
锐角三角形
直角三角形
钝角三角形
等腰三角形
等边三角形
扇形有什么特征呢?
圆上任意两点之间的部分叫做弧。读作“弧AB”。
一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形,图中涂色部分就是扇形。
你想到了我们学过的哪些图形?
这些图形的共同特点是什么?
都是由四条直的边围成的图形,都有4个角。
你会给这些四边形分类吗?
做两个一样的平行四边形纸片。把它们重合在一起,将上面的平行四边形绕它的一个顶点旋转180°,再通过平移使它与下面的平行四边形重合。观察两个平行四边形的各条边与各个角,你有什么发现?
1.判断对错,对的画“√”,错的画“×”。
(1)大于90°的角就是钝角。( )
(2)两条直线相交组成的4个角中如果有一个角是直角,那么其他3个角也是直角。( )
(3)任何两个等底等高的梯形都能拼成一个平行四边形。( )
×
√
×
2.在括号里填上合适的计量单位。
km
m2
kg
L
1. 过一点可以画几条直线?过两点可以画几条直线?
无数条
一条
2. 有长度分别为3cm、4cm、5cm、6cm的小棒各一根。哪三根小棒可以围成一个三角形?
3cm、4cm、5cm
4cm、5cm、6cm
3cm、5cm、6cm
3cm、4cm、6cm
三角形任意两边的和大于第三边
3. 一个直角三角形的两个锐角的和是多少度?为什么?
90度。三角形内角和减去一个直角得到两个锐角的和。
锐角三角形的两个锐角和一定大于90°,钝角三角形的两个锐角和一定小于90°。
同学们,今天的数学课你们有哪些收获呢?
1.我会填。
(1)经过一点可以画( )条直线,经过两点可以画( )条直线。
(2)如图,共有( )条直线,( )条射线,( )条线段。
无数
1
1
8
6
(3)一个多边形的内角和是540°,它是( )边形。
(4)(2019·浙江宁波)如图,三角形ABC中,∠A=70°,如果沿图中的虚线剪去∠A,∠1+∠2=( )°。
五
250
2.我会选。(将正确答案的序号填在括号里)
(1)把一张圆形的纸对折两次,折出的角是 ( )角。
A.锐 B.直 C.钝
(2)已知一个三角形的两条边分别长4cm和8cm,那么第三条边可能是( )。
A.12cm B.15cm C.11cm
B
C
(3)下面的角不能用一副三角尺直接画出的是( )。
A.15° B.55° C.75°
B
3.如图,已知∠1=30°,求∠2、∠4和∠5的度数。
∠2=90°-∠1=90°-30°=60°
∠4=180°-∠2-∠3
=180°-60°-90°
=30°
∠5=90°-∠4=90°-30°=60°
