苏教版高中数学选修2-2《复数的运算》课件(共26张PPT)
文档属性
| 名称 | 苏教版高中数学选修2-2《复数的运算》课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 974.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-02-25 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
复数的四则运算
数系的扩充
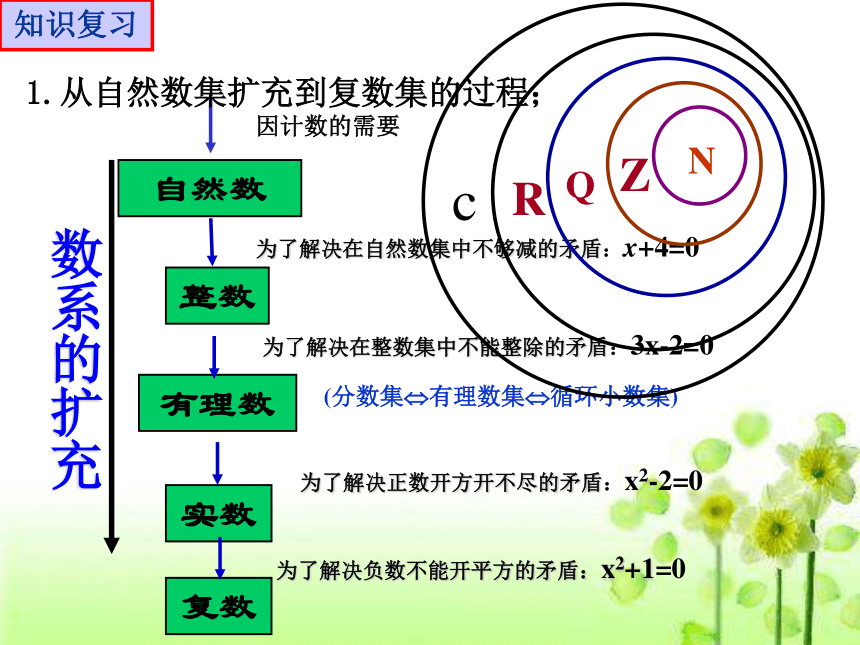
自然数
实数
因计数的需要
为了解决在自然数集中不够减的矛盾:x+4=0
为了解决在整数集中不能整除的矛盾:3x-2=0
(分数集?有理数集?循环小数集)
1.从自然数集扩充到复数集的过程;
为了解决负数不能开平方的矛盾:x2+1=0
知识复习
为了解决正数开方开不尽的矛盾:x2-2=0
2.复数有关概念:
复数的代数形式:
复数相等:
复数的分类:
虚数单位i的引入
知识复习
1.复数加减法:
运算法则:设复数z1=a+bi,z2=c+di,
那么:z1+z2=(a+c)+(b+d)i;
z1-z2=(a-c)+(b-d)i.
即:两个复数相加(减)就是实部与实部,虚部与虚部分别相加(减).
探究:复数加减的结果所满足的形式说明什么?
复数的和与差还是复数
(2)复数的加法满足交换律、结合律,即对任何z1,z2,z3∈C,有
z1+z2=z2+z1,
(z1+z2)+z3=z1+(z2+z3).
例1.计算
例题分析
2.复数的乘法
(1)复数乘法的法则
复数的乘法与多项式的乘法是类似的,但必须在所得的结果中把i2换成-1,并且把实部合并.即:
(a+bi)(c+di)=ac+bci+adi+bdi2
=(ac-bd)+(bc+ad)i.
探究:复数相乘的结果所满足的形式说明什么?
复数的积还是复数
(2)复数的乘法满足交换律、结合律以及乘法对加法的分配律.
即对任何z1,z2,z3有
z1z2=z2z1;
(z1z2)z3=z1(z2z3);
z1(z2+z3)=z1z2+z1z3.
【探究】 i 的指数变化规律
你能发现规律吗?有怎样的规律?
例2:计算
思考:设x,y为实数,在实数集R内,x2+y2能否被因式分解?
那在复数集C内呢?
例题分析
在复数集范围内因式分解
当堂训练
说明:
共轭复数:
实部相等而虚部互为相反数的两个复数,叫做互为共轭复数,也称这两个复数互相共轭。
定义:
思考:设z =a+bi (a,b∈R )
2.实数的共轭复数是什么?
概念辨析
B
D
当堂反馈
待定系数
拓展提高
评析:对于复数问题,若从整体上去观察、分析题设结构,
充分利用复数的有关概念等,能收到简捷明快的效果
三、知识新授:
分母实数化
四、例题应用:
先写成分式形式
化简成代数形式就得结果.
然后分母实数化即可运算.(一般分子分母同时乘以分母的共轭复数)
例5:
归纳总结
1.复数的加减法运算法则
2.复数的乘法运算法则
z1+z2=(a+c)+(b+d)i
z1-z2=(a-c)+(b-d)i
(a+bi)(c+di)= (ac-bd)+(bc+ad)i.
4.共轭复数及相关性质(特别关注ω)
5.掌握待定系数法及整体思想
3. i 的指数变化规律
课本:P118
课本:P119
复数的四则运算
数系的扩充
自然数
实数
因计数的需要
为了解决在自然数集中不够减的矛盾:x+4=0
为了解决在整数集中不能整除的矛盾:3x-2=0
(分数集?有理数集?循环小数集)
1.从自然数集扩充到复数集的过程;
为了解决负数不能开平方的矛盾:x2+1=0
知识复习
为了解决正数开方开不尽的矛盾:x2-2=0
2.复数有关概念:
复数的代数形式:
复数相等:
复数的分类:
虚数单位i的引入
知识复习
1.复数加减法:
运算法则:设复数z1=a+bi,z2=c+di,
那么:z1+z2=(a+c)+(b+d)i;
z1-z2=(a-c)+(b-d)i.
即:两个复数相加(减)就是实部与实部,虚部与虚部分别相加(减).
探究:复数加减的结果所满足的形式说明什么?
复数的和与差还是复数
(2)复数的加法满足交换律、结合律,即对任何z1,z2,z3∈C,有
z1+z2=z2+z1,
(z1+z2)+z3=z1+(z2+z3).
例1.计算
例题分析
2.复数的乘法
(1)复数乘法的法则
复数的乘法与多项式的乘法是类似的,但必须在所得的结果中把i2换成-1,并且把实部合并.即:
(a+bi)(c+di)=ac+bci+adi+bdi2
=(ac-bd)+(bc+ad)i.
探究:复数相乘的结果所满足的形式说明什么?
复数的积还是复数
(2)复数的乘法满足交换律、结合律以及乘法对加法的分配律.
即对任何z1,z2,z3有
z1z2=z2z1;
(z1z2)z3=z1(z2z3);
z1(z2+z3)=z1z2+z1z3.
【探究】 i 的指数变化规律
你能发现规律吗?有怎样的规律?
例2:计算
思考:设x,y为实数,在实数集R内,x2+y2能否被因式分解?
那在复数集C内呢?
例题分析
在复数集范围内因式分解
当堂训练
说明:
共轭复数:
实部相等而虚部互为相反数的两个复数,叫做互为共轭复数,也称这两个复数互相共轭。
定义:
思考:设z =a+bi (a,b∈R )
2.实数的共轭复数是什么?
概念辨析
B
D
当堂反馈
待定系数
拓展提高
评析:对于复数问题,若从整体上去观察、分析题设结构,
充分利用复数的有关概念等,能收到简捷明快的效果
三、知识新授:
分母实数化
四、例题应用:
先写成分式形式
化简成代数形式就得结果.
然后分母实数化即可运算.(一般分子分母同时乘以分母的共轭复数)
例5:
归纳总结
1.复数的加减法运算法则
2.复数的乘法运算法则
z1+z2=(a+c)+(b+d)i
z1-z2=(a-c)+(b-d)i
(a+bi)(c+di)= (ac-bd)+(bc+ad)i.
4.共轭复数及相关性质(特别关注ω)
5.掌握待定系数法及整体思想
3. i 的指数变化规律
课本:P118
课本:P119
